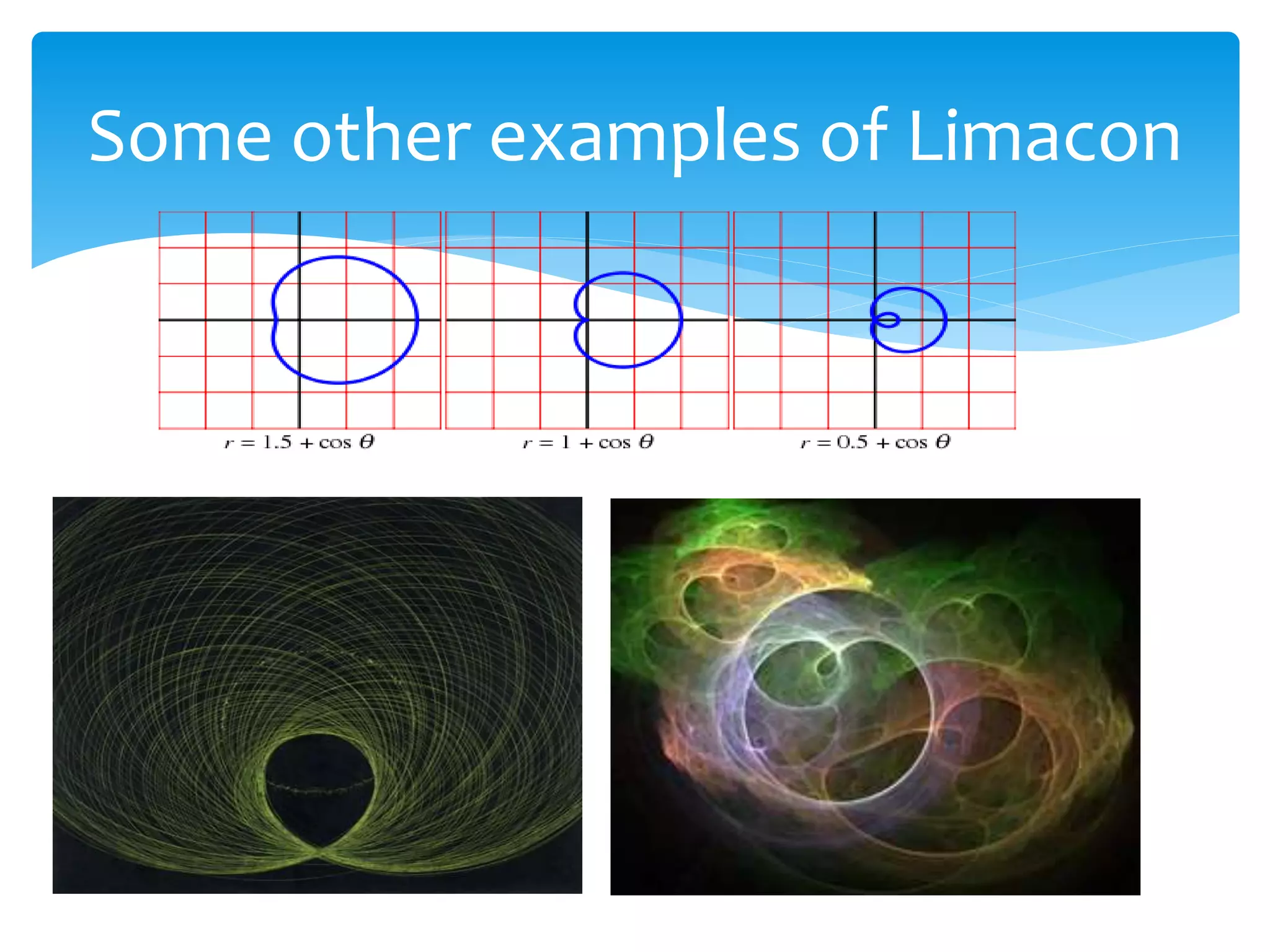
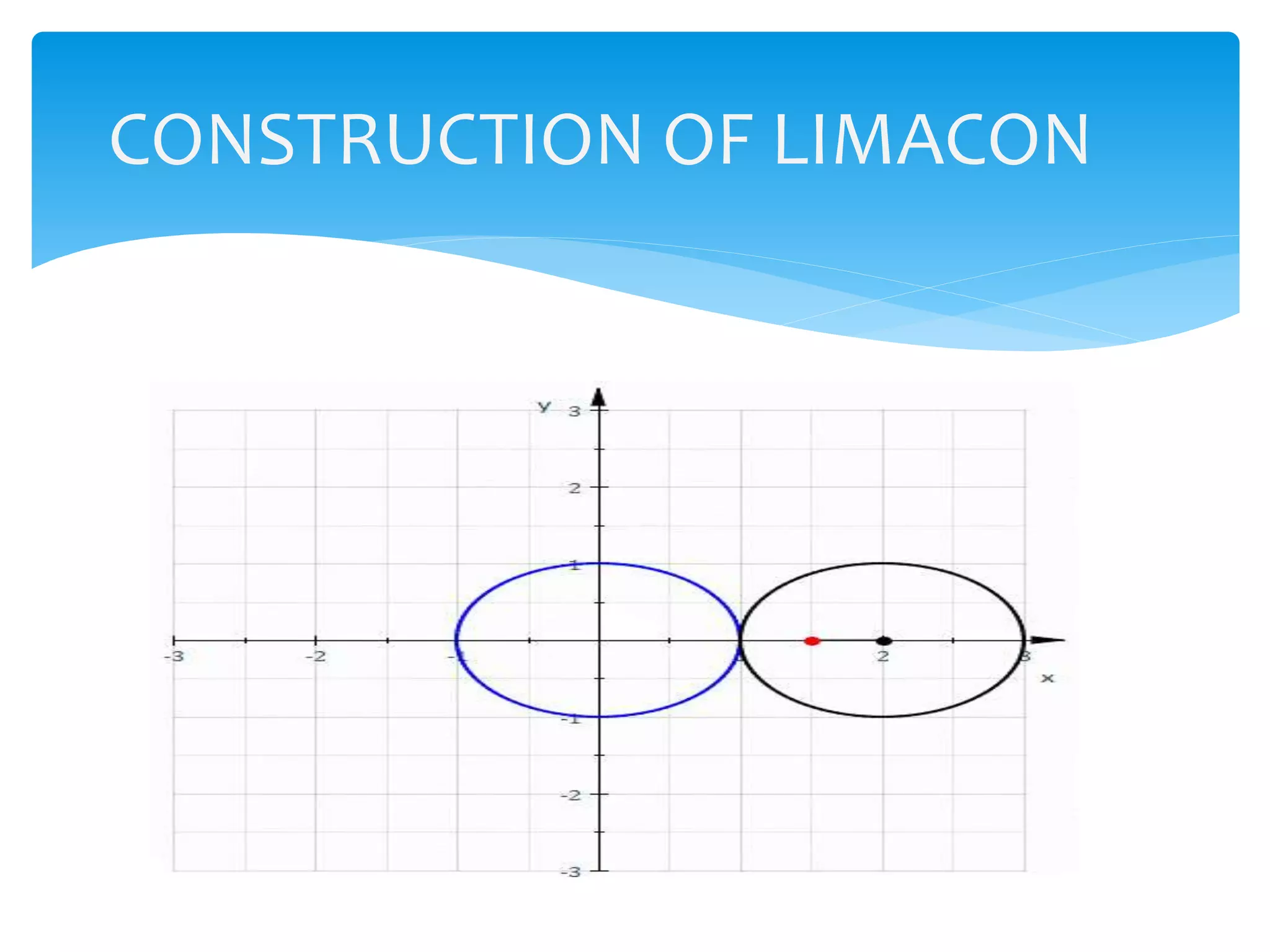
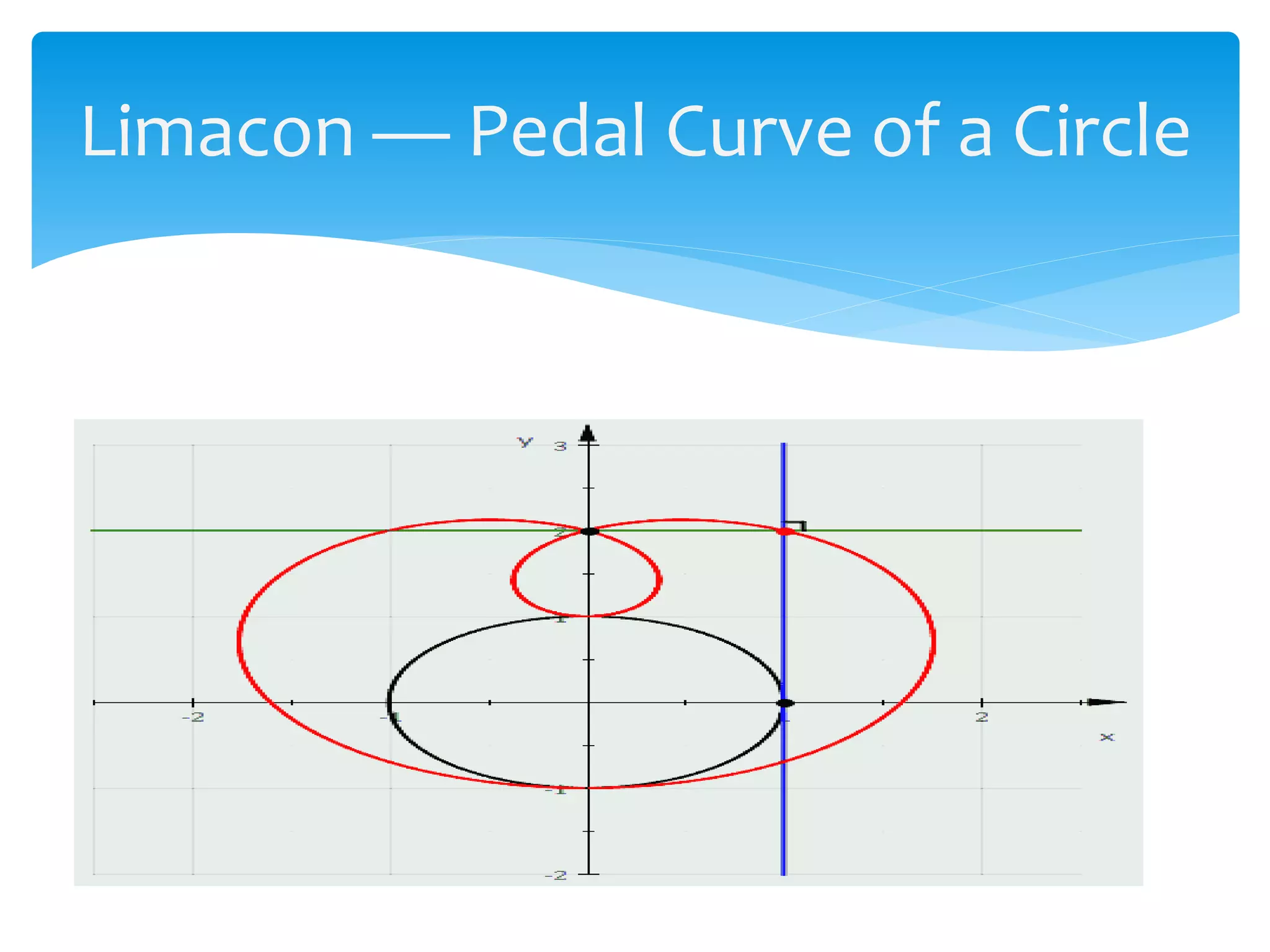
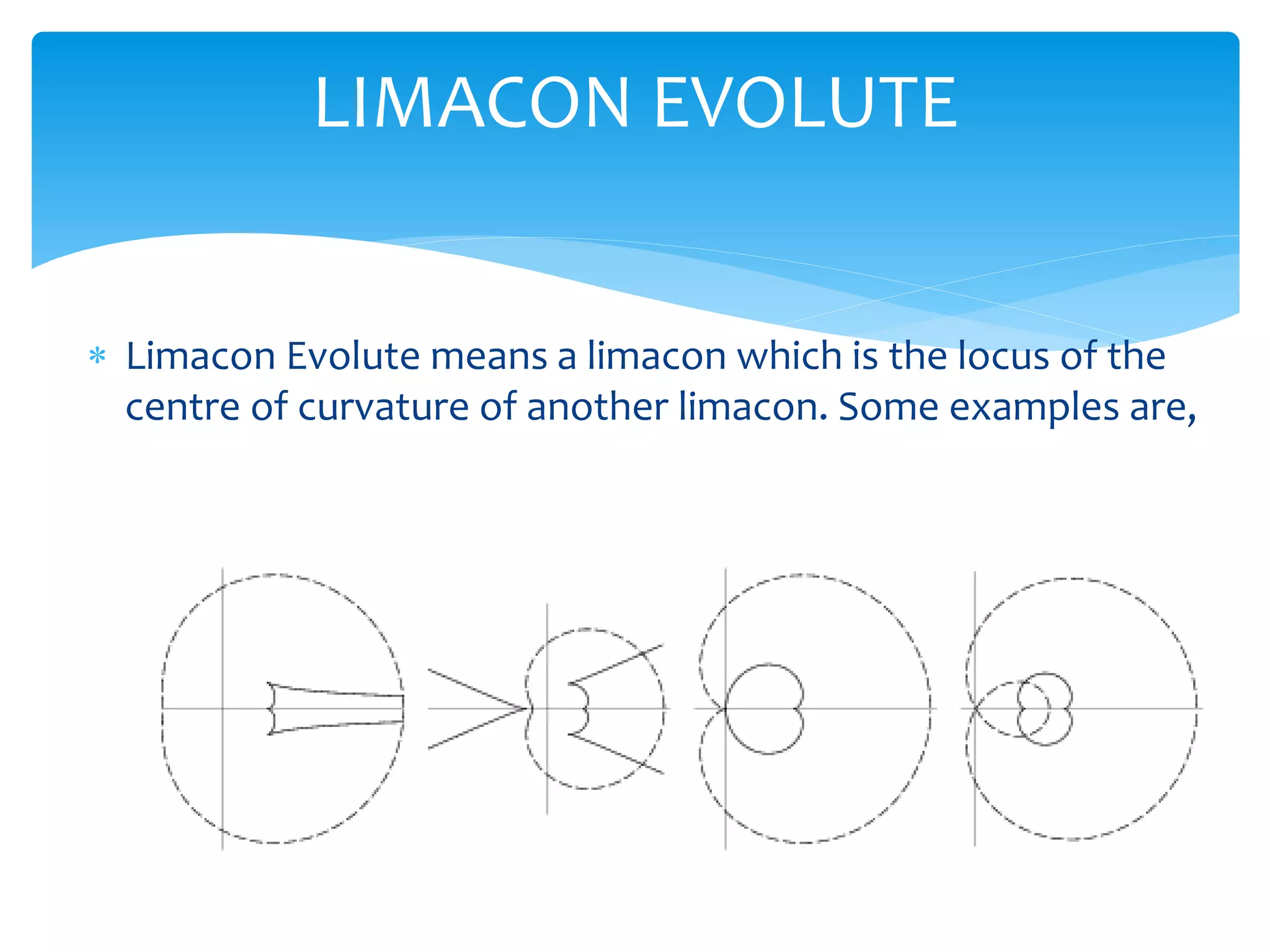
The document discusses the limacon, a polar curve defined by the equation r=b+acosθ, detailing its historical origins, properties, and different forms based on parameters a and b. It explains conditions for its shapes, such as being convex, dimpled, or having an inner loop, and provides equations related to its area and arc length. Additionally, references and examples of the limacon are included, highlighting its significance in mathematics.

1. CALCULuS
LIMACON

2. FANTASTIC FOUR
PRESENTS
1.MOHIT BALHARA
2.UTKARSH ANAND
3.ABHISHEK CHIIKARA
4.HARIKESH KUMAR

3.  The Limacon is a polar curve of the form having
Equation r=b+acosΘ
 Cartesian Equation (x2 + y2 - 2ax)2 = b2(x2 + y2)
 Some basic curves of limacon.
INTRODUCTION

4. Some other examples of Limacon

5.  Limacon is also called the Limacon of Pascal. It was
first investigated by Dürer, who gave a method for
drawing it in book Underweysung der
Messung (1525). It was rediscovered by Étienne
Pascal, father of Blaise Pascal, and named by Gilles-
Personne Roberval in 1650 (MacTutor Archive).
 The word “Limacon" comes from the Latin limax,
meaning "snail."
HISTORY

6.  As we know the equation of Limacon is r=b+acosѲ
 In it, If,b>=2a the Limacon is convex.
 If, 2a>b>a the Limacon is dimpled.
 If, b=a the Limacon degenerates to a cardioid.
 If, b<a the Limacon has an inner loop.
 If, b=a/2 it is a trisectrix.
SOME BASIC CONDITIONS

7. The first one is the concaved.
Second one is dimpled.
The third one is cardioid.
CONSTRUCTION OF LIMACON

8. Limacon — Pedal Curve of a Circle

9.  For , the inner loop has area.
=
=
=
where .
AREA OCCUPIED BY LIMACON

10.  For , the outer loop has area
=
=
=
Area Contd.

11.  Thus, the area between the loops is
 But there is a special case for b = a/2
Area Contd.

12.  In the special case of b=a/2 , these simplify to
Area Contd.
=
=
=

13.  The parametric form of Limacon is:
x= (b + a cos t) cos t
y = (b + a cos t) sin t
gives the arc length s(t) as a function of t as
where E(z,k) is an elliptic integral of the second kind.
PARAMETRIC FORM

14.  Let t=2𝜋 gives the arc length of the
entire curve as
 where E(k) is a complete elliptic integral
of the second kind.
Contd.

15.  Limacon Evolute means a limacon which is the locus of the
centre of curvature of another limacon. Some examples are,
LIMACON EVOLUTE

16.  The catacaustic of a circle for a radiant point is the limacon
evolute.
It has parametric equations.
=
=
Contd.

17. en.wikipedia.org/wiki/Limaçon
http://mathworld.wolfram.com/Limacon.html
http://www-history.mcs.st-and.ac.uk/Curves/Limacon.html
 www.mathwords.com/l/limacon.htm
BIBLIOGRAPHY

18. THANK YOU