Binary Search

1. Binary Search
Let ai 1≤ i ≤ n be a list of elements that are
sorted in non decreasing order.
Consider the problem of determining
whether a given element x is present in
the list. If x is present , we are to
determine a value j such that aj = x. If x is
not in the list , then j is to be set to zero

2. Iterative Binary Search
Algorithm BinSearch(a,n,x)
{
low:=1;high:=n;
while( low ≤ high) do
{
mid:=(low+high)/2;
if(x<a[mid]) then high:=mid -1;
else if (x>a[mid])then low:=mid+1;
else return mid;
}
return 0
}

3. Recursive Binary Search
Algorithm BinSearch(a,i ,I ,x)
//Given an array a[i:l]of elementsin nondicreasing
//order 1i≤l,determine whether x is present
{
if (l=i) then
{
x=a[i] then return i;
else return 0;
}else
{
mid:=(i+l)/2;

4. if(x=a[mid]) then return mid ;
else if (x<a[mid])then
return Binsrch(a,i,mid-1,x);
else return Binsrch(a, mid+1,l,x);
}
}

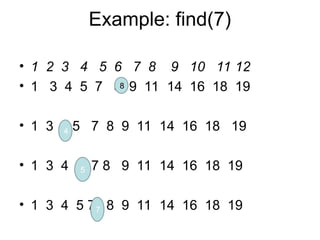
5. Example: find(7)
• 1 2 3 4 5 6 7 8 9 10 11 12
• 1 3 4 5 7 8 9 11 14 16 18 19
• 1 3 4 5 7 8 9 11 14 16 18 19
• 1 3 4 5 7 8 9 11 14 16 18 19
• 1 3 4 5 7 8 9 11 14 16 18 19
8
4
5
7

6. • Example:-
-15, -6, 0, 7, 9, 23, 54, 82, 101,
112,125, 131, 142,151
X=151 low high mid
1 14 7
814 11
1214 13
14 14 14
found that a[14]=151

7. 7
3 11
5
9
8
13
12
14
6
4
2
10
1

8. If n is in the range [2k-1
2k
),then BinSearch
makes at most k elements of comparison
for successful search and either k-1 or k
comparison for an unsuccessful search. In
other words time for successful search is
O(log n) and for an unsuccessful search is
(log n)