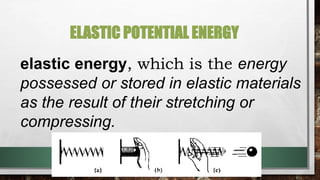
- Energy is the ability to do work and exists in various forms such as potential and kinetic energy. Potential energy is the stored energy of an object due to its position or state. - Gravitational potential energy is the energy possessed by an object due to its height and is calculated as PE = mgh. Elastic potential energy is the energy stored in stretched or compressed springs and is calculated as PE = 1/2kx^2. - Examples are provided to demonstrate calculating the gravitational and elastic potential energy of various objects based on their mass, height, spring constant, and displacement from equilibrium.

2. ENERGY
•ENERGY IS THE ABILITY TO DO WORK.
LAW OF CONSERVATION OF ENERGY
“ENERGY CAN NEITHER BE CREATED NOR
DESTROYED BUT CAN ONLY BE CONVERTED OR
TRANSFORM FROM ONE FORM TO ANOTHER”

3. THE WORK – ENERGY THEOREM AND
KINETIC ENERGY

4. THE WORK – ENERGY THEOREM AND
KINETIC ENERGY

5. POTENTIAL ENERGY
Potential energy is the stored energy of
an object due to its positions
(configurations) within its system. This
energy is not an individual particle but
rather a property of the system.

6. GRAVITATIONAL POTENTIAL ENERGY
THE ENERGY POSSESSED BY A BODY AS THE
RESULT OF ITS POSITION OR CONFIGURATION
(HEIGHT) IS CALLED GRAVITATIONAL POTENTIAL
ENERGY. ENERGY CAN BE STORED IN AN OBJECT TO
BE ABLE TO DO WORK, WE CAN RELATE ENERGY
AND WORK AS A SIMILAR ENTITY.

7. GRAVITATIONAL POTENTIAL ENERGY
𝑊𝑒𝑥𝑡 = 𝐹𝑒𝑥𝑡𝑑 COS 0°=𝑚𝑔ℎ= 𝑚𝑔(𝑦2 − 𝑦1).

8. Gravity is also acting on the object as it
moves from y1 to y2, and does work on it
equal to
𝑊𝐺 = 𝐹𝐺 𝑑 cos 𝜃 = 𝑚𝑔ℎ 𝑐𝑜𝑠 180°
where θ = 180° because 𝐹𝐺 and 𝑑⃗ point
in opposite directions. So
WG = - mgh = - mg (y2 - y1)

9. The gravitational potential energy stored
in the elevated object is equal to the
work done in raising the object to a
certain height. The work done is
equivalent to the weight of the elevated
object multiplied by the distance to
where it is elevated.
So, we define gravitational potential
energy (GPE) mathematically as
𝑷𝑬𝒈𝒓𝒂𝒗 = 𝒎𝒈𝒉

10. 𝐺𝑃𝐸 = 𝑚𝑔ℎ , also in this way:
𝐺𝑃𝐸 = 𝑤𝑒𝑖𝑔ℎ𝑡 𝑥 ℎ𝑒𝑖𝑔ℎ𝑡
where weight: 𝑤 = 𝑚𝑔
The higher an object is above the ground,
the more gravitational potential energy it
has. We have
Wext = mg (y2 – y1)
Wext = PE2 – PE1 = ΔPE.

11. On the other hand, we can write the
change in potential energy, ΔPE, in
terms of the work done by gravity
itself, we obtain
Wgrav = - mg (y2 – y1)
Wgrav = - (PE2 – PE1) = - ΔPE

12. Sample Problem 1.
A cart is loaded with a brick and pulled
at constant speed along an inclined
plane to the height of a seat-top. If the
mass of the loaded cart is 5.5 kg and
the height of the seat top is 1.08
meters, then what is the potential
energy of the loaded cart at the height
of the seat-top?

13. Given: m = 5.5 kg
h = 1.08 m
g = 9.8 m/s2 = ag (acceleration due to gravity)
Unknown: GPE = ?
Formula: GPE = mgh
Solution:
= (5.5 kg) (9.8 m/s2) (1.08m)
= (53.9 kg·m/s2) (1.08 m)
= (53.9 N) (1.08 m)
Answer: = 58.21 J

14. Sample Problem 2.
Find the gravitational potential energy of
the books in Figure given that the weight
of each book is 12 N.
Unknown:
GPE1 = ?
GPE2 = ?
GPE3 = ?

15. Given: W = 12 N
h1 = 4.5 m
h2 = 3 m
h3 = 1.5 m
Solution:
GPE1 = (12 N) (4.5 m) = 54 J
GPE2 = (12 N) (3 m) = 36 J
GPE3 = (12N) (1.5 m) = 18 J
Answer:
GPE1 = 54 J
GPE2 = 36 J
GPE3 = 18 J
Formula: GPE = mgh

16. ELASTIC POTENTIAL ENERGY
Whenever an object is moved from one
point to a second point, the change in
potential energy associated with a
particular force is equal to the negative of
the work done by that force. We can this
equation,
W = - (PE2 – PE1) = - ΔPE

17. ELASTIC POTENTIAL ENERGY
elastic energy, which is the energy
possessed or stored in elastic materials
as the result of their stretching or
compressing.

18. A simple coil spring is shown in Figure, which
possesses potential energy when compressed or
stretched, it can do work on a ball when it is
released.
In figure, an amount x from its natural(unstretched)
length requires the hand to exert a force on the
spring FP, which is directly proportional to x. That is
FP = kx
where k is a constant, called spring stiffness
constant, and is a measure of the stiffness of the
particular spring.

19. FS = - kx.
FP is the force exerted by
the hand
FS is the resisting force
(opposite force exerted
by the hand)

20. In calculating the potential energy of a stretched spring, take
note that the
force is changing or varies over some distance, it will also
greater as the spring stretched more. So let’s use the average
force, F, since FP varies linearly – from zero at the equilibrium
position (the position in which there is no applied force on it,
typically an assumption of natural position) to kx; when
stretched to x – the average force is F = ½ [0+kx] = ½ kx, where x
here is the final amount stretched (i.e. xi = 0 at equilibrium
position and x in kx is equal to xf ). The work done is

21. ELASTIC POTENTIAL ENERGY IS PROPORTIONAL
TO THE SQUARE OF THE AMOUNT STRETCHED:
𝑷𝑬𝒆𝒍𝒂𝒔𝒕𝒊𝒄 = 1/𝟐 𝒌𝒙2

22. Sample Problem.
A spring has a constant force of 15 N/m. What is the
PEelastic of the spring when it is stretched a distance of
0.80 m?
Given:
k = 15 N/m
x = 0.80 m
Unknown: PEelastic = ?

23. Formula: PEelastic = ½ kx2
Solution: = ½ (15 N/m) (0.80 m2)
= ½ (15 N/m) (0.64 m2)
= ½ (9.6 N·m)
= 4.8 N·m
Answer: = 4.8 J

24. Sample Problem.
A coiled spring in a sweat belt requires a force of
33 N to compress it by 25 cm.
(a) Find the spring constant of the coiled spring.
(b) How much force is needed to compress the
spring by 50 cm?
(c) What is its potential energy when compressed
by 50 cm?
Answers must be in meters (m).

25. Solution:
(a) F = 33 N
x = 25 cm = 0.25 m
k = ?
(b) To compress the spring by 50 cm (0.50 m) the force
needed will be
F = (132 N/m) (0.50 m)
= 66 N
𝑘 = 𝐹/𝑥
= 33 𝑁/ (0.25 𝑚)
= 132 𝑁/m
(c) Its elastic potential energy
= ½ kx2 is
PEelastic = ½ (132 N/m) (0.50 m)2
= ½ (132 N/m) (0.25 m2 )
= ½ (33 N·m)
= 16.5 N·m
= 16.5 J