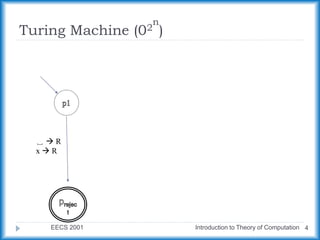
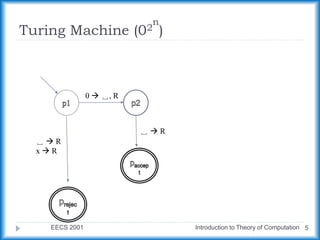
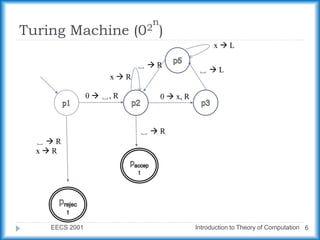
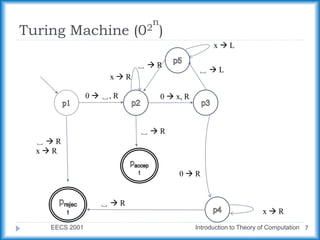
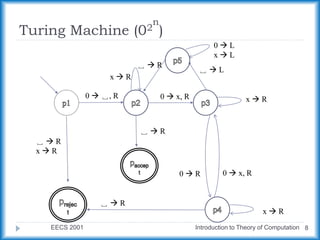
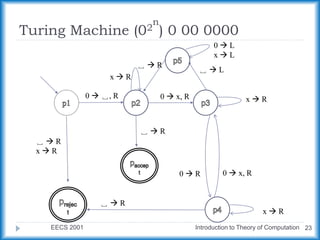
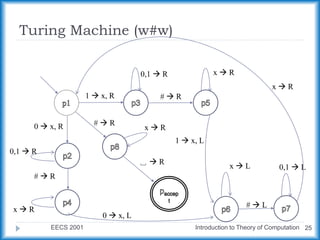
The document describes a Turing machine that accepts strings of zeros with a length of a power of two. It does this by repeatedly crossing off every second zero, from left to right, until there is only one zero remaining or an odd number of zeros remain. If only one zero remains, the string is accepted, and if an odd number remain, the string is rejected. An example run is shown for the input string "0000".