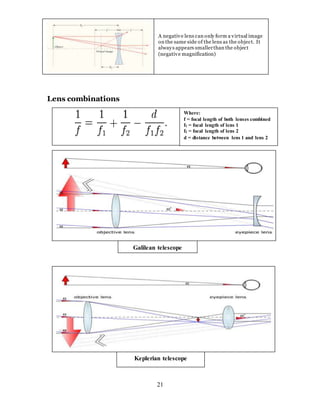
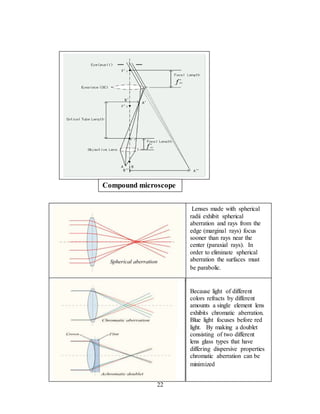
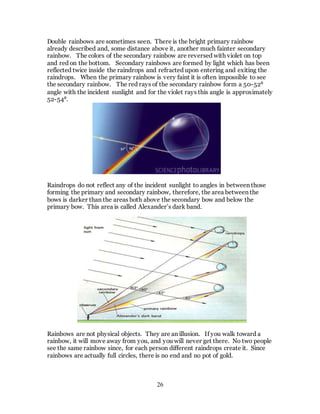
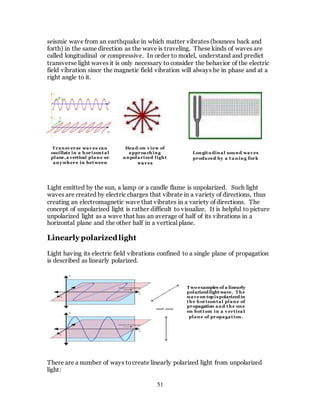
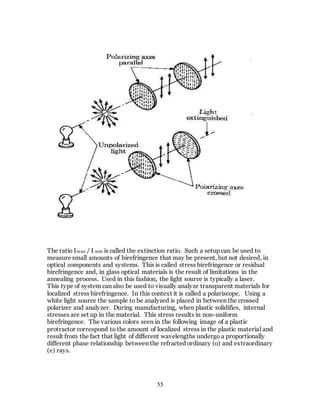
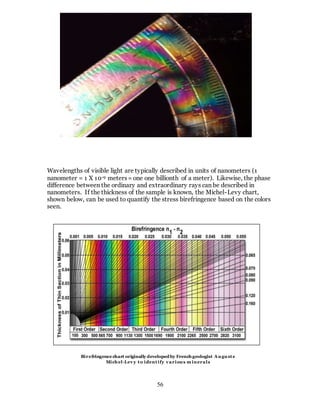
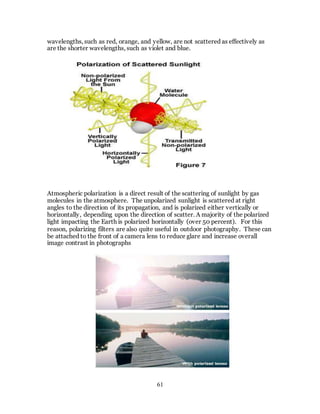
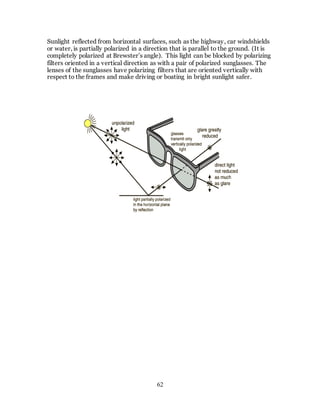
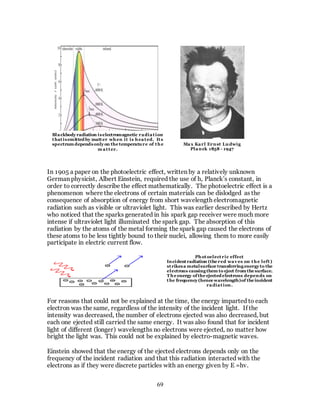
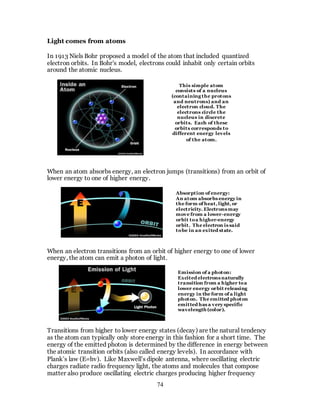
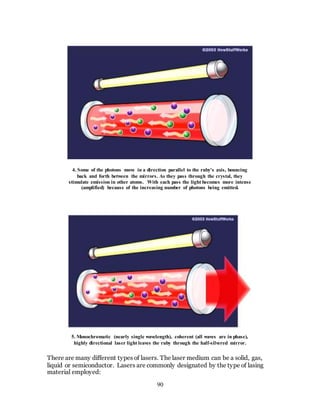
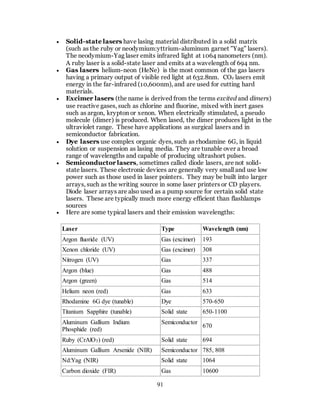
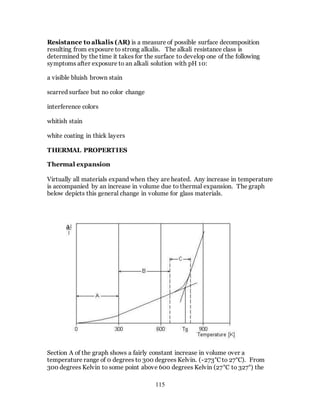
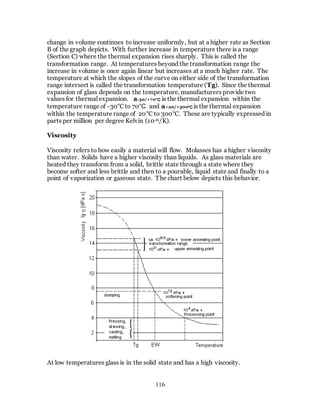
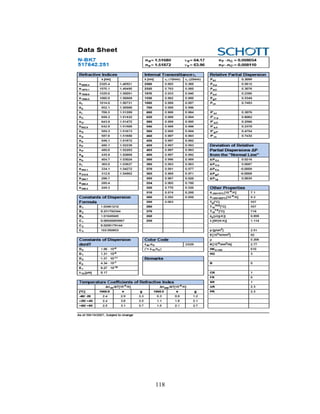
1. The document discusses the history and evolution of optics from ancient times to the 11th century CE. It describes how early civilizations like the Greeks, Chinese, and Phoenicians made early observations and experiments with light, lenses, mirrors, and vision. 2. The work of the ancient Greek philosophers such as Euclid, Ptolemy, and Aristotle helped develop early theories of light, but it was not until the 11th century Arab scholar Ibn al-Haytham (Alhazen) that many modern theories of vision and optics began to take hold. Through experiments with lenses, mirrors, and the camera obscura, Alhazen helped debunk earlier theories and establish that light travels in straight lines

1. 1
FOREWARD
The study of optics is the study of light. Everybody is familiar with light. Without
it, we don’t see, plants don’t grow and our notions of time and space fade into
abstraction. Light is all around us. An estimated 30% of our waking brainpower
is used to interpret the light images that fall on our retinas. It is the main vehicle
to our perception of reality providing us with the visual clues that aid us in
survival. Light also acts physically in our world, providing warmth from the sun
and the fuel required for photosynthesis, the process that sustains plants so that
they can grow and reproduce. Without light there would be no complex life on
Earth.
As early man stepped out of the cave, he became aware of light in its various
manifestations. He marveled at the blue sky and the spectacle of the rainbow.
He watched the sun on its daily path through the heavens and its descent beyond
the horizon, as it gave way tonight. He contemplated the night sky with its
moon, planets and tiny points of light called stars. He discovered that by
observing the shadow cast by a stick mounted vertically in the ground, he could
know the time of day and predict the procession of the seasons through the year.
Prehistoric monuments like Stonehenge, at Wiltshire, England and the pyramids
of Egypt and Mexico and other structures around the world are undeniable
evidence that the ancients deduced much about their world through keen and
sustained observations of the “lights” in the sky. These monuments, constructed
from around 4000 BCE, are built with such precise alignment with astronomical
events, that to consider this coincidence would be absurd.
As time passed, prehistoric civilizations attained varying levels of understanding
in many branches of knowledge, and then faded without leaving written records
of their achievements. Glass used for jewelry and drinking vessels was made on a
large scale by the Phoenicians along the eastern coast of the Mediterranean as
early as 3500 BCE. The first mention of the use of lenses for starting fire was by
the Greek writer, Aristophanes, in about 425 BCE. Writing at about the same
time, Chinese philosopher Mo Tzu described reflection from flat and curved
mirrors. It is the ancient Greek philosophers, though, that have provided history
with written records of their observations and speculations. It is there, then that
we begin to retrace the evolution of human thought regarding the nature of light
and the science of optics.
Stonehenge monument Ancient Egyptian sundial The greatpyramid atCheops

2. 2
What is optics ?
The word “optics” is derived from the Greek word for “seeing” or “of the eye”.
Optics is the branch of physics which involves the behavior and properties of
light, including its interactions with matter.
Optics is also the word used to describe actual components and instruments used
to control or measure light, such as eyeglasses, prisms, mirrors and telescopes.
Optics also describes the industry of manufactured products used to manage
light. When someone asks “What kind of work do you do?” no doubt, the word
“optics” is part of your answer.
Please note that the first definition pertains to the science of light and attempts
to understand and explain its behavior where the other definitions pertain to the
technology of manipulating light to achieve some useful purpose. Advances in
the science, or understanding of light have enabled advances in optical
technology, leading to the invention of new and better products. Likewise,
advances in optical technology have often led to a better scientific understanding
of the nature of light. In order to understand optics we must first understand
light.
What is light? How does it work?
Geometrical optics - rays
The true nature of light has been a subject of intrigue and debate for over 2500
years. The oldest written records we have of speculations on the nature of light
are from the ancient Greeks, although they seem a lot more interested in how we
see than what light actually is. Empedocles, Plato, and Euclid believed that vision
is enabled by a “visual ray” that flowed out of the eyes and engaged objects in
such a way that your mind can perceive them. Democritus and others known as
the atomists believed that everything was made of tiny indivisible particles called
atoms. This included light. They reasoned that vision is possible because objects
shed atoms that peel off the object’s surface in very thin layers, maybe one atom
thick, called “eidola”. These are somehow able to pass through the eyes and into
the mind. Aristotle taught that light is “the activity of transparent media” like air
and water. Note that this is in contrast to the atomists who considered light to be
composed of tiny atoms, therefore, a substance. Aristotle’s idea was that light
was a disturbance of transparent matter, an accidental property. Aristotle also
taught that anything that “moves” is moved by something else. By “move” he
means any kind of change. There is, therefore, no empty space. Even though we
can not see it, there must be this “something” in order for causes to result in
effects at a distance. For instance, the stars and planets that eternally circle
around the earth are pushed by this invisible substance. Aristotle called this

3. 3
substance “ether”. Euclid, the father of geometry, showed that light travels in
straight lines and described the relationship between the apparent sizes of objects
and the angles that they subtend at the eye. Toward the end of the Greek heyday,
the astronomer Ptolemy wrote about the reflection of rays from flat and curved
mirrors and correctly stated the law of reflection, that is, that light reflects from a
smooth surface at the same angle at which it strikes the surface. He also
investigated the bending of rays that go from air to water, air to glass and water
to glass. Being much more of an experimenter than most other Greek
philosophers he invented an apparatus to measure this angle and derived a table
that showed a mathematically simple, albeit incorrect, relationship between the
direction the ray was going (angle of incidence) and the direction it changed to
upon entering a different medium (angle of refraction) based on constant
proportions. Although, at small angles his mathematical model was very close to
what really happens, at larger angles his constant proportion becomes less
accurate. Ptolemy is best known for his work in astronomy and for his maps of
the known world of his time. Like Aristotle before him, he taught that the Earth
was at the center of the universe surrounded by crystal spheres that held the
moon, planets, sun and stars. He created maps of the stars and planets that were
used to navigate ships. Ptolemy’s model of the universe was accepted for nearly
1500 years after his death.
With the decline of the Roman Empire in 411 CE, Europe descended into a so
called “dark age” where scientific progress stopped. Many of the ancient world’s
libraries had been destroyed and most of the Greek writings lost. Early Christian
church teachings emphasized eternal salvation as the most important aspect of
existence, and matters of the physical world as fleeting and temporary.
GREEK PHILOSOPHERS (approx. 500 BCE to 500 CE)

4. 4
Fortunately, many of the surviving writings of the Greek thinkers were translated
into Arabic by Islamic philosophers. In about 1000 CE, the ideas of Aristotle,
Euclid and Ptolemy along with original thinking by Islamic philosophers like Al
Kindi and Ibn Sahl, came to the attention of one Abū Alī al-Ḥasan ibn al-Ḥasan
ibn al-Haytham who is known to the Western world as Alhazen. His experiments
with the camera obscura, which had been observed and described by Aristotle,
led him to a new theory of vision. He rejected the idea of eidola and visual rays
and wrote that light from the sun, or some other light source, reflects from an
object’s surface and travels in straight lines to our eyes traveling through the
pupils. Essentially, he took the straight-line visual rays described by Euclid and
turned the arrows around. He believed that vision takes place in the eye’s crystal
lens, since, beyond that location the image would be inverted as it is in the
camera obscura. His writings include descriptions of the structure and the image
formation function of the eye.
Alhazen also investigated reflection from flat and curved mirror surfaces. He
found that concave mirrors having a spherical surface do not bring all incident
rays toa focus at the same point. Alhazen pointed out that images formed by
spherical mirrors are distorted and that those formed using parabolic surfaces
would be free from this distortion. This is now called spherical aberration and is
also a limitation to images formed using spherical lenses. He also studied
magnification using lenses and repeated Ptolemy’s refraction experiments. He
found that Ptolemy’s table and law of constant angle proportion was incorrect,
but was unable to find the actual mathematical relationship. This would not be
officially discovered for another 600 years. He speculated that light has a finite,
although incredibly fast speed and that it travels slower in water than it does in
air. This turned out to be the case. Alhazen advocated experimentation as the
method of understanding the physical world. This is in contrast to most of the
Greek philosophers who believed that truth can only be arrived at through rigid
logic stemming from previously proven “facts”. Alhazen is known as the “Father
of optics”.
Abū Alī al-Ḥasan ibn al-Ḥasan ibn al-Haytham
ALHAZEN (approx 965 – 1060 CE)
The First Scientist
The Father of Optics
Demonstrating the camera obscura
Alhazen’s diagram
of an eye
Explained how a camera obscura works.
Vision happens because light that is reflected from objects forms an
image in our eyes much like a camera obscura.
Measured refraction in glass and water. Found that Ptolemy’s
constant proportion angle was incorrect. Speculated that light travels
slower in glass and water than it does in air.
Estimated the thickness of the atmosphere by timing twilight and
applying what he learned about refraction.
As Christianity spread throughout Europe, the church felt it necessary to
document what it is that Christians believe. In the 13th century many clergymen
were involved in translating the Arabic translations of ancient Greek texts into

5. 5
Latin. The philosophies of Aristotle were the most aligned with church teachings,
so his ideas were very influential in establishing Christian scientific beliefs.
Robert Grosseteste, while he was Bishop of Lincoln in England, wrote a number
of scientific works on such topics as the calender, the tides, geometry, Aristotle
and light. In his book, De Luce, which means On Light, he describes a universe
that was created entirely from light. When God said, “Let there be light” a huge,
but finite flash of light traveled outward in all directions. This created the three
dimensions of space. When the light went as far as it could, it created the outer
sphere (the firmament), and returned inward, creating the spheres that hold the
stars, planets and moon. Finally, as it reached the center it formed the four
elements that make up the earth. (Earth, Water, Air and Fire). This has been
called the medieval “big bang” theory. Grosseteste believed that light is the
essential means of physical causation and that optics is the fundamental science.
He also taught that it is only through geometry and mathematics that we can
begin to understand nature.
Roger Bacon wrote Opus Majus, Opus Minus and Opus Tertium, a virtual
encyclopedia of the accumulated known science of his age. He emphasized the
“scientific method” of inquiry, that is; forming a hypothesis, testing the
hypothesis through experimentation and deriving conclusions based on the
results. It is suggested, from his writings, that Roger Bacon was the first person
to make spectacles for himself and may have experimented with microscopes and
telescopes, but there is no direct physical evidence. Opus Majus includes
discussions of the physiology of eyesight with diagrams showing the anatomy of
the eye and the brain, and discusses distance, position, and size of objects in
relation to vision. It also includes descriptions and sketches showing reflection
from mirrors and refraction and magnification using lenses. His writing on
optics is largely based on Alhazen’s work.
The main contributions of Grosseteste, Bacon and other medieval Christian
writers was to advance the scientific method of inquiry bringing Europe out of the
so-called dark ages and paving the way for scientific progress.
From the 14th tothe 17th century Europe underwent a renaissance, meaning
“rebirth” that started in Italy and spread throughout Europe. It was a cultural
movement that encompassed a blossoming of literature, art, education and
RobertGrosseteste 1175 - 1253 Roger Bacon 1220 - 1292

6. 6
politics. In art, paintings were being produced that actually look like real scenes.
Prior to this, most paintings were without depth and attempted to capture an
emotion or to mark an event. Renaissance paintings incorporated perspective
which was discovered by analyzing how light rays from varying distances travel to
the eyes. Many artists actually used mirrors, camera obscuras and other optical
tricks to aid them in their craft. This was the age of Leonardo DaVinci, William
Shakespeare, Johan Gutenberg and Christopher Columbus.
Also, just before his death, in 1543, the Polish astronomer Nicolas Copernicus
published his book, On the Revolutions of the Celestial Spheres. In it, he
proposed that the sun, rather than the earth, was at the center of the universe,
and that the earth and other planets revolve around it. This idea would not
become widely accepted for another 150 years as it was at odds with Church
doctrine which seemed to require that the earth be the center of the universe.
Although it is not specifically about light or optics, when the Copernican system
became accepted as true, it opened the door for insights into the nature of light
based on correct astronomical observations. Copernicus’ epiphany is identified
as a defining moment that ushered in what has been called the scientific
revolution.
Copernicus – Conversation with God (Jan Matejko 1872)
School of Athens- Raphael.
Painted in 1510-1511, thisreflects the
Italian Renaissance pa ssion for
classical antiquity depicting som e of
the greatest figures from Greek
history, such asPlato and Aristotle.
Raphael gave them the faces of his
contemporaries,like Michelangelo.
The painting's use of single vanishing
pointperspective,mastery of figures,
and choice of subjectmattermark this
as a work of the High Italian
Renaissance

7. 7
During this era new ideas in physics, mathematics, astronomy, biology, chemistry
and other sciences were explored and began to transform human knowledge.
Prevailing scientific knowledge handed down from the Greeks and medieval
thinkers came under question and were ultimately replaced by knowledge
acquired through deployment of the scientific methods advocated by Alhazen,
Roger Bacon and others.
The beginning of the 17th century saw the invention of both the telescope and the
microscope. It is not clear who the actual inventors were, but a Dutch spectacle
maker named Hans Lippershey is often given credit for inventing the telescope.
He applied for a patent from the Dutch government and received a commission
to build one. Others came forward to claim that they had already constructed
such a device, but were unable to demonstrate it. Although the credit for these
inventions is debatable their impact to scientific advancement, particularly in the
case of the telescope, was immediate and profound.
Italian physicist,mathematician and philosopher Galileo Galilei is the name that
we most often associate with the telescope. Having heard of the invention he
began to build and sell telescopes and used them to explore the night sky. Galileo
was the first to observe that Jupiter has moons that revolve around it, that the
moon’s surface was full of craters and that the Milky Way is actually comprised of
billions of stars. His observations eventually led to a belief in the heliocentric
(sun-centered) system advanced by Copernicus. In his book, Dialog Concerning
the Two Chief World Systems, Galileo states the case for a sun-centered universe
based on his observations and the fact that it explains these observations so much
better than the Ptolemic system does. For his beliefs, Galileo was found guilty of
heresy by the Roman Inquisition. He was forced to recant his opinion and spent
the last 9 years of his life on house arrest. In 1992, 350 years after Galileo’s
death, Pope John Paul II officially apologized and acknowledged the church’s
error.
Galileo, with an assistant, once attempted tomeasure the speed of light by the
following method: he and the assistant stood on hills that were several
kilometers apart. Each had a lantern and a means of blocking the light from it.
Galileo uncovered his lantern and began counting. When the assistant saw the
light from Galileo’s lantern he unblocked his. By timing how long it took to make
the round trip, one should be able to calculate light’s speed. All that Galileo was
able to conclude was that light traveled very fast, much faster than the time it
takes for humans to respond to a visual stimulus. Galileo later became the first
curator of the Royal Society, an organization devoted to the advancement of
science. Although his contributions to the understanding of light were minimal,
Galileo’s work helped to reshape our concept of the cosmos and our place in it.

8. 8
Johannes Kepler was a German astronomer, astrologer and mathematician.
Kepler designed a type of telescope having higher magnification than those made
by Galileo using two positive lenses. He discovered that the orbits of the earth
and other planets were actually elliptical, rather than circular, with the sun at one
focus of the ellipse. Applying careful observation and mathematical analysis,
Kepler showed that the velocity of planets as they race around the sun changes
inversely as their distance from the sun changes. This was an important
discovery that played a major role in Newton’s later formulation of the laws of
universal gravitation. In optics, Kepler discovered what is called the inverse
square law, that the intensity of light is reduced by the square of the distance
from the light source.
Kepler performed an experiment scraping the fatty tissue from the back of an ox’s
eyeball until a very thin, translucent layer remained. Pointing the eyeball toward
a scene, he observed an inverted image of the scene that traveled through the
pupil and projected onto the retina, much like the image formed by a camera
According to the Inverse Square law the
intensity oflight is geometrically related
to the distance traveled. In the equation
given,I is the intensity ofthe radiation at
one unit distance (1d). At two unit
distances (2d),the intensity ofthe
radiation is determined by dividing I by
the square ofthe new distance from the
source. T he same procedure is used to
determine the intensity at three unit
distances from the source.
Fresco by Giuseppe Bertini depicting
Galileo showing the Doge of Venice
how to use the telescope Johannes Kepler 1571 - 1630

9. 9
obscura. The fact that the image was inverted did not bother Kepler as it did
Alhazen, who, because of this, believed that vision actually took place in the
crystal lens, rather than the retina. Kepler considered the mind’s ability to
interpret light rays as a purely mental construct. This, he explained, is why the
image of an object reflected in a mirror appears to be at the same distance behind
the mirror as the distance that the object actually is from the front of the mirror.
Kepler also investigated how lenses change the direction of light rays. People had
used lenses to start fires and magnify things since antiquity. For nearly two
centuries, spectacles had improved vision for elderly and nearsighted individuals.
Now people were using telescopes to see farther and microscopes to see smaller.
The problem was that nobody really understood how lenses worked. Kepler
showed that images formed by lenses were constructed point by point from light
rays reflected from an object. From every point of the object’s surface, an infinite
number of rays pass through the lens which changes the direction of these rays in
a manner that produces an image of the object. Distinguishing between real and
virtual images Kepler described mathematically how lenses, telescopes and
microscopes work. He also discovered total internal reflection.
Although Kepler’s biggest contributions to science were in the field of astronomy,
his contribution to optics cannot be understated. He described the behavior of
light rays in mathematical terms forming the basis for the principles of
geometrical optics. What makes Kepler’s discoveries even more amazing is that
they were accomplished without really knowing the laws that govern the amount
T he perception ofthe distance ofan
object in a mirror is due to the brain’s
interpretation ofthe direction oflight
rays reflected from the mirror.
Every pointon the tree
contributes an infinite
number oflight rays that are
reconstructed by the lens to
form an image.

10. 10
a light ray is bent (refracted) as it passes from one medium to another. His
calculations were based on the tables that originated with Ptolemy and later
improved upon by Alhazen and Roger Bacon.
It seems that the correct law of refraction was discovered independently by two
men working about the same time. These men were Rene Descartes and
Willebrod Snell.
Rene Descartes was a true renaissance man who frequently set his views apart
from his predecessors. He is best known for his philosophical and mathematical
works and has been called the father of modern philosophy. In mathematics he
introduced methods of representing shapes in three dimensions using algebraic
expressions. This is known as Cartesian geometry.
In optics, Descartes postulated a theory of light describing it as a mechanical
pressure on the eyes that is transmitted through a space filled with tiny hard
particles he called the plenum. Although his theory is easily dismissed,
something like the plenum later became known as ether and was to become a
necessary part of subsequent theories of light. Descartes also provided the
correct relationship that describes the law of refraction, although it required that
light travels faster in water and glass than it does in air, which, it turns out, is not
the case.
Willebrod Snell was a Dutch astronomer and mathematician. He invented a new
method for measuring the diameter of the earth and for calculating π. (π - pi is a
mathematic constant equal to a circle’s circumference divided by its diameter).
Descartes Law of Refraction: The ray AB and BC have traveled for the
same amount of time. Since light travels faster in glass or water than it does
in air, ray BC is longer, but lines AP and QC are equal because the change
in speed only applies in the direction perpendicular to the surface

11. 11
Snell’s law of refraction was derived experimentally and based strictly on
geometric analysis. His law of refraction was Snell’s only contribution to optics.
There was significant controversy regarding who found the law of refraction first,
Descartes or Snell. In France it is still called Descartes’ law. The rest of the world
calls it Snell’s law. Some scholars believe that Descartes plagiarized Snell’s work.
It is now also believed that an Islamic scientist named Ibn Sahl may have
discovered the correct law of refraction in about 984CE.
In 1657, French mathematician, Pierre de Fermet stated a principle of least time
from which one could derive Snell’s law, as long as one assumes that light travels
slower in glass and water than it does in air. This principle also describes the law
of reflection (the angle of incidence equals the angle of reflection).
Refraction was now understood nearly as well as reflection.
Snell’s Lawof refraction: For any angle of incidence, i, the refracted angle, r is such
that the ratio of di/dr is always the same. di/dr is called the index of refraction. For
water the index is approximately 1.33. For glass it is about 1.5
Fermat’s principle or the principle of least
time is the principle that the path taken
between twopoints by a ray of light is the path
that can be traversed in the least time.
Fermat's principle can be used todescribe the
direction of light rays reflected off mirrors.

12. 12
Ole Roemer was a Danish astronomer who studied the orbit of Jupiter’s moons.
One of these moons, Io, revolves around Jupiter in about 42 hours. He was
hoping that this could provide a method of keeping accurate time at sea. This
was one of the most challenging problems of the day, as many ships were lost at
sea. (It was eventually solved by an English clockmaker, John Harrison, in 1759).
Roemer noticed that when earth was approaching Jupiter, Io disappeared behind
the huge planet sooner than expected. Each day it was eclipsed slightly sooner
than the previous day. When earth was receding from Jupiter the opposite
occurred. Each day Io disappeared slightly later than the previous day. The
reason was immediately clear to Roemer, and, enlisting the help of Dutch
mathematician, Christian Huygens, he set about calculating the speed of light
based on the diameter of the earth’s orbit and the measured time differences in
Io’s eclipses. In 1676, using the best estimate of earth’s orbit available at the time
he came up with a value of 220,ooo,ooo meters per second, about two thirds of
today’s accepted value. Not bad for the first try!
Although the compound (multi-lens) microscope was invented around 1590, its
impact to science was not as immediate as was the telescope. A Dutch lensmaker
named Zacharias Jensen is usually given credit, although this is a matter of
debate.
Robert Hooke was a Professor of geometry but also held a post as the curator of
experiments for the Royal Society. In this capacity he acquired a great deal of
theoretical and experimental knowledge in many aspects of science including
biology, physics and architecture. In his book, Micrographia (Small Pictures),
Hooke provided sketches of what he saw using the compound microscope that he
designed. He is the first person to use the word “cell” to describe the make-up of
plant and insect structure. This became the most popular science book of it’s
time inspiring Antony van Leeuwenhock who produced an enormous amount of
work uncovering the unknown microscopic world. Although he never published
any books, van Leeuwenhock wrote many letters tothe Royal Society describing

13. 13
and making sketches of his many discoveries. His work paved the way for an
understanding of the bacterial causes of disease and began the science of
microbiology.
Hooke’s book also contained some speculations on the nature of light and color.
He believed that light is the result of the vibration of the particles that compose
matter. These vibrations form ripples in the air that surrounds an object, and,
the color of light depends on which edge of the vibrations enter the air first,
either red or blue. All other colors are a mixture of red and blue. Thus, color is a
modification of light and not a property of it. Hooke came to these conclusions
by observing the colors produced by very thin mica sheets and the thin layer of
air trapped between two glass sheets. His reasoning here becomes very difficult
to follow, but it was obvious that these phenomena begged two questions:
1) What is colored light
2) How does it differ from white light?
Isaac Newton attempted toanswer these questions.
Sir Isaac Newton was one of the most influential scientists in human history. His
work shaped the views of physics and mathematics for over two centuries. In his
book, Principia, he established the three laws of motion and universal gravitation.
He showed that Kepler’s elliptical planetary orbits are easily explained using
these principles, thus removing all doubt about the reality of the heliocentric
planetary system. He also studied sound, heat, Biblical prophecy and history and
developed calculus. It is his work in Optics, though, that is of interest here.
In 1664, while at a local fair, Newton purchased a glass prism. It had the cross-
sectional shape of an equilateral triangle. It had been known for some time that
such a prism could produce a rainbow of colors, but these were thought to be the
result of some kind of tinting that the glass did to the light, much like colored
stained glass. These were sold mainly as toys, not investigative instruments. It
was experimentation with prisms that led Newton to all his other work in optics.
Hooke’s microscope
Flea
Louse
Blue fly
Mold growingon a
rose leaf

14. 14
Newton made a small hole in his window blind, allowing a thin beam of sunlight
to enter his otherwise darkened room. He placed the prism into the beam and
positioned it so that the colored beam was seen on the opposite wall. As he
observed the pattern of colored light he noticed that the shape of it was oblong
rather than circular. Along the long axis of the oblong shape, the color fanned
out from violet to red with red being the closest to the location of the original
sunbeam before the prism was placed in its path. Nothing known about the
refraction of light could explain this. The only way he was able explain it was if
the prism somehow bent light of different colors to different angles, violet
bending the most and red bending the least. In this way, he reasoned that the
white light of the sun is actually made up of all the colors of the rainbow. In
order to test this theory, Newton performed what he called the “critical
experiment”. He placed a wooden board with a small hole in it in front of the
colored beam. By rotating the prism he could allow only one color at a time to
pass through the hole. He placed a second prism in the path of the single colored
light and found that the light pattern on the wall was now circular and that the
prism produced no further colors. For extra measure, Newton then removed the
wooden sheet and adjusted the second prism to a position where he was able to
recombine the colored ray back into a white circle of light on the wall. Newton
had discovered dispersion. This is the principle that light of different colors
refract by differing amounts when passing from one medium to another.
Although this occurs as sunlight passes through a window we do not see it,
because when the rays exit the window and return to air they are bent in the
opposite direction and the colored light is recombined. In the case of the prism,
because of its geometry, the light continues to bend in the same direction.
Newton continued to experiment with his prism and found that he could mix
different colored light to produce new colors. For instance, when he mixed
yellow with blue he produced green. These were not completely mixed, though,
because he could once again separate them with a prism. He called these
compounded colors.
From colored light, Newton moved on to the color of objects. He found that an
object having a certain color, when illuminated by a different color of light, takes
on the color of the light. When illuminated by light of the same color, the object
appears in its normal color. For instance, a red apple looks its normal red when
illuminated by red light. When illuminated by blue light it nearly looks black.
From this Newton deduced that the color of objects is due to selective absorption
and reflection. The apple absorbs all the other colors of white light to a greater
extent than it does red and reflects red light to a greater degree than it does the
other colors.
Newton continued to report the results of his experiments presenting these to the
Royal Society. In these writings Newton suggested that light was composed of a
stream of particles that he called “corpuscles”. It was many years after Newton’s
work in optics was done that his book Optiks, was published. It summed up his
optical experiments and presented many queries regarding light that inspired
future generations of physicists. In it one sees that Newton wasn’t as committed

15. 15
to the idea of light particles as was thought and often uses words like “fits of easy
transmission and reflection” to describe diffraction and “oscillations of light rays”
to described the colors seen in Hooke’s mica sheets.
The principle and a model of Newton’s reflecting telescope.
Dispersion –light of different colors refract by different amounts with red bending the least and
violet bending the most. A material’s refractive index depends on the color of the light being
refracted.
Having discovered that the refraction of light through glass is different for different
colors, Newton invented and built a reflective telescope that uses two mirrors instead
of lenses. This eliminated the blur of color (chromatic aberration) seen in refractive
telescopes.

16. 16
RAY OPTICS PHENOMENA
Specular reflection
FROM A PLANE SURFACE
FROM CURVED SURFACES
The reflection of MountHood in Trillium Lake.
Spheresreflectingthe floor and each other.
Specular reflection ata curved surface formsan image whichmay be magnified (concave) or reduced (conv ex).
For all reflected ray s of a concav e m irror to focus at the sam e point requires a parabolic surface.
T he angle of incidence equals the angle of reflection. T he reflected ray is in the same
plane as the incident ray and the normal to the surface.

17. 17
Total internal reflection
-
Critical angle, I =
A Black triggerfish reflecting from the water surface
The critical angle, i = sin-1 (n2 / n1) where n1 > n2

18. 18
Frustratedtotal internal reflection
Diffuse reflection
When light thatwould otherwise undergo totalinternalreflection encountersa surface in contact or
v ery close to the boundary between the highindex and lowindex materials som e of the light passes
throughthe highindexsurface. In the sketch on the right, as distance d is decreased m ore light
propagates into the prism on the right
Diffuse reflection occurswhen light encountersa rough surface. The rays scatter in alldirections and do
not form an im age. Most objects are seen by v irtue of diffuse reflection.

19. 19
REFRACTION
Through a plane parallel glass plate (Beam adjuster,tilt
block)
When a light ray encounters a boundary
between two media having different
refractive indexes the direction ofthe ray
changes according to Snell’s law: Sin i (ni) =
sin r (nr) where:
i = the angle ofincidence
r = the angle ofrefraction
ni = the refractive index ofmedium 1
nr= the refractive index ofmedium 2
T he refractive index ofa medium is defined as
the speed of light in a vacuum ©divided by
the speed of light in the medium.
θa = θ’a
d = t sin (θa – θ’b) / cos θ’b

20. 20
Through a plane wedged glass plate
Through lenses
.
Lensmaker’s formula
1/f = (n-1) [1/R1 – 1/R2 + (n-1)d/nR1R2]
where
f is the focal length ofthe lens,
n is the refractiveindex ofthe lens
material,
R1 is the radius ofcurvatureofthe
lens surface closest to the light
source,
R2 is the radius of curvatureofthe
lens surface farthest from the light
source,and
d is the center thicknessofthe lens
(the distance along the lens axis
between the two surface vertices).
Light from an object that is at a distance
beyondthe lens focal length forms a real
image on the side of the lens opposite the
object. Magnification (reduction) ofthe
image is S2 / S1. For an objectat infinity (or
very far away from the lens) the image will be
a small focused spot.
Light from an object that is at a distance less
than the lens focal length forms a virtual
image on the same side of the lens as the
object. Magnification ofthe image is S2 / S1.
This is the principle ofa magnifying glass.

21. 21
Lens combinations
A negative lens can only form a virtual image
on the same side of the lens as the object. It
always appears smallerthan the object
(negative magnification)
Galilean telescope
Keplerian telescope
Where:
f = focal length of both lenses combined
f1 = focal length of lens 1
f2 = focal length of lens 2
d = distance between lens 1 and lens 2

22. 22
Compound microscope
Lenses made with spherical
radii exhibit spherical
aberration and rays from the
edge (marginal rays) focus
sooner than rays near the
center (paraxial rays). In
order to eliminate spherical
aberration the surfaces must
be parabolic.
Because light of different
colors refracts by different
amounts a single element lens
exhibits chromatic aberration.
Blue light focuses before red
light. By making a doublet
consisting of two different
lens glass types that have
differing dispersive properties
chromatic aberration can be
minimized

23. 23
Beam steering with prisms
Small wedge (Risley) prisms change the
direction of a light ray. For wedge angles less
than 10 degrees:
Beam deviation = (n – 1) wedge angle
Where n is the refractive index.
Right angle
prisms can
change beam
direction by 90
degrees (fold
prism) or 180
degrees (porro
prism).
Retroreflectors (corner cube) change
beam direction 180 degrees sending light
back in the direction it came from.

24. 24
HOW A RAINBOW WORKS
Sunlight, which appears white, is really composed of a mixture of red, orange,
yellow, green, blue and violet light. Raindrops are almost spherical, held in shape
by the force of surface tension acting on their surfaces. When sunlight hits a
round raindrop it refracts according to Snell’s law as the light passes from air to
water. Due to differing amount of refraction for each color, the white light begins
to separate into its component colors as it passes through the raindrop. This is
called dispersion, which Isaac Newton investigated and explained using a glass
prism. The diverging rays of colored light then travel tothe back of the raindrop
where they are reflected at the water toair interface, according to the law of
reflection (the angle of reflection equals the angle of incidence). The colored rays
then pass back through the front of the raindrop, below the point where the
sunlight first entered, and are again refracted at the water to air interface. This
causes further separation of the colors. The colored rays emerge near the bottom
of the drop with the red ray, at the bottom, making an angle of 42⁰ with the
incident sunlight. The violet ray, on top, makes a 40⁰ angle with the incident
sunlight. The blue, green, yellow and orange rays appear, in that order, in
between the violet and red. The rays of sunlight that contribute to the primary
rainbow are those that enter raindrops at a location that is near the top. In the
picture on the right below, if the radius of the raindrop is 1R, then the rays that
enter at a distance that is 0.85R from the center toward the top are the rays that,
after two refractions and one reflection, form the rainbow.
Alaskan rainbow – with visible secondary bow

25. 25
The size of raindrops influences brightness of the colors we see. The brightest
rainbows appear when drop diameters are between 0.3 and 1 millimeter. If drop
diameters are larger than 1 millimeter, red, orange, and yellow colors are bright
but blue and violet are dim. When the drops are smaller than 0.3 millimeters, the
red and orange color bands are dimmer and the blue and violet are brighter.
Very small raindrops, less than about 30 microns (0.03 millimeters) produce
rainbows that are faint and appear almost white. These are sometimes called
fogbows.
For a rainbow to be seen, certain conditions are necessary. The day must be
sunny and the Sun low in the sky. If the sun is more than 42⁰ above the horizon
the rainbow will be formed below the opposite horizon and not seen. The lower
the sun is the higher the arch of the rainbow will be. The best times are in the
morning or evening when the sun is near the horizon. It is not possible to see a
rainbow while facing the Sun. Rainbows are always seen in the part of the sky
opposite from where the sun is. This part of the sky must contain a quantity of
raindrops as what occurs during or after a rain. The most vibrant rainbows are
seen when this part of the sky contains dark rain clouds providing a background
having more contrast with the colored light. A rainbow is formed by millions of
raindrops acting at once, but only one color from each drop actually reaches the
observer’s eyes. Raindrops that are lower in the sky direct the violet rays tothe
observer. The same observer will see the blue rays from raindrops that are higher
in the sky, the green from raindrops that are even higher and so on through
yellow orange and red. This is why the primary rainbow has the red arc on top
and the violet at the bottom.
The reason that the rainbow is a curved part of a circle is that each colored arc of
the rainbow is formed by raindrops that have a specific angular relationship
between the sun and the observer. For instance, the red arc of the rainbow is
formed by all the raindrops that are 42⁰ from the observer tothe center of the
rainbow, called the antisolar point. The antisolar point is located by imagining a
line drawn from the sun, through the observer’s head and to a point usually
below the horizon. All the raindrops that are at 42⁰ from the imaginary line to
the antisolar point form the red circle. Likewise, each colored arc of the rainbow
is a part of a circle formed by those raindrops located at the specific angle for that
color. Usually, at least half of the circle is below the horizon and can not be seen.
Rainbows seen from a high hill or from an airplane may include more, or even all,
of the lower half of the full circle.

26. 26
Double rainbows are sometimes seen. There is the bright primary rainbow
already described and, some distance above it, another much fainter secondary
rainbow. The colors of the secondary rainbow are reversed with violet on top
and red on the bottom. Secondary rainbows are formed by light which has been
reflected twice inside the raindrops and refracted upon entering and exiting the
raindrops. When the primary rainbow is very faint it is often impossible to see
the secondary rainbow. The red rays of the secondary rainbow form a 50-52⁰
angle with the incident sunlight and for the violet rays this angle is approximately
52-54⁰.
Raindrops do not reflect any of the incident sunlight to angles in between those
forming the primary and secondary rainbow, therefore, the area between the
bows is darker than the areas both above the secondary bow and below the
primary bow. This area is called Alexander’s dark band.
Rainbows are not physical objects. They are an illusion. If you walk toward a
rainbow, it will move away from you, and you will never get there. No two people
see the same rainbow since, for each person different raindrops create it. Since
rainbows are actually full circles, there is no end and no pot of gold.

27. 27
Occasionally, when a shower happens at sunrise or sunset, the shorter
wavelength violet, blue and green have been scattered by earth’s atmosphere and
partly removed from the incident sunlight. Further scattering may occur due to
the rain, and the result can be the rare and dramatic red rainbow, also called a
monochrome rainbow.
Photograph of a red (monochrome) rainbow.

28. 28
Physical optics - Waves
Newton’s writings were given to Robert Hooke, the curator of the Royal Society’s
experiments, for his opinion. Hooke stated that although the experiments were
beautifully performed, they do not prove that white light is made up of different
colors. Hooke has misunderstood Newton to say that white light is made of small
particles having different colors. He challenges Newton to mix up powders of
different colors to produce white. Hooke then claims that the vibration theories
discussed in his book, Micrographia can explain Newton’s experimental results, if
one assumes that light is nothing but a pulse, or motion and color a disturbance
of that motion.
What Hooke was talking about was waves, although he never used that word. A
similar theory of light was previously proposed by a Jesuit priest, Francesco
Maria Grimaldi in his Treatise on Light, published after his death in 1663. In it
he describes experiments that he performed that showed that objects do not
produce sharp shadows and, at the edge of the shadow the light tends to creep,
ever soslightly into the shadowed area. Additionally, a narrow band of colored
light could be seen in the transition between the fully lighted and fully shadowed
areas. Grimaldi called this effect diffraction (Latin for “break into pieces”). His
explanation for it suggested that light was something like a stream of fluid. When
it encounters an object it becomes disturbed sending ripples through the air
much like sound waves.
Newton was quick to respond. He knew that sound waves were a disturbance of
air molecules that propagated from a source to an ear by transferring a pattern of
alternating compression and decompression of the air itself. He suggested that
anyone who believes that light is a wave has two big problems. For one, what is it
that is waving? A wave is only an influence. Sound waves and water waves both
require a medium to act upon. Secondly, sound waves can bend around corners.
If I am around a corner from you, I can still hear you, although I can’t see you.
(Grimaldi’s experiment seemed to show that light does bend around corners a
little bit, but Newton dismissed that as some physical property of the edge itself.)
Grimaldi’s experimental
set-up
Grimaldi’s sketch ofcolored bands
at the edge of a shadow
Diffraction at the edges
of a razor blade
Francesco Maria
Grimaldi 1618 - 1663

29. 29
Dutch scientist Christian Huygens was the main champion for a wave theory of
light. He considered how two light beams, like sound waves, can pass through
one another without either one affecting the other. He argued that if light was
composed of particles one would expect that they would occasionally collide and
be sent off in another direction. Huygens arrived at his pulse wave theory of light
by observing waves in water. His ideas were described in his Treatise on Light,
written in 1678 and published in 1690. In it he described how light waves are
propagated through a substance he called ether. The ether fills all of space and is
the medium that is doing the waving. It is similar to Descartes’ plenum except
the subtle particles comprising it are springy rather than hard. For Huygens light
is matter in motion. Sources of light, such as the sun or fire, consist of particles
that vibrate, transferring their motion to the ether. These start off as a chaotic
pulse disturbance of ether particles called wavelets and are much like the circular
ripple of waves that is seen when a pebble is dropped into a body of still water.
The motion of these wavelets is transferred to adjoining ether particles in all
directions. In the direction away from the source they combine to create a
wavefront. In the direction sideways to the source they tend to cancel each other
out. Each point along the wavefront is considered to be a source of new wavelets
that eventually combine to form the next wavefront and in this manner the light
is propagated through the ether. Huygens went on to explain how his light waves
can explain reflection and refraction and the recently discovered phenomena of
diffraction.
Even though the idea of light waves received the support of a few other thinkers,
such as the eminent mathematician, Leonard Euler, it would be more than 100
years before they were given serious consideration. That was a shame, because
light waves have a lot going for them.
Christian Huygens (1625 – 1695)

30. 30
HUYGENS WAVE MECHANICS
Huygens’ depiction of the
refraction of a plane wavefront
Huygens’ depiction of the
propagation of a spherical
wavefront
Huygens’ depiction of the
reflection of a plane wavefront
Diffraction of a plane wave
passing through an aperture.
In 1801, Thomas Young performed his famous double slit experiment. Young
passed a source of monochromatic (one color) light through a pair of very narrow
slits spaced close to each other. He observed that as light passed through the
slits it “fanned out” demonstrating that light does bend around edges (diffract).
Not only that, Young also observed light interference, which cannot be explained
by particle theory. Lightwaves, like water waves, interact with each other.
Where the high points or crests of one wave meet the crests of another wave the
localized intensity of the light (or height, in the case of water waves) is the sum of
the intensity of the crests. Where the crests of one wave meet the low points, or
troughs of another wave, the two cancel each other and the localized intensity is
zero. In Young’s experiment this interference was observed as a pattern of bright
and dark bands (fringes) projected onto a screen placed some distance beyond
the slits. Young speculated that the color of light is due to its wavelength with red
light having the longest wavelength and violet light having the shortest. In
Young’s mind, lightwaves, like sound waves, were longitudinal. This means that
they travel in ether by causing alternating compression and decompression of
ether particles. The back and forth oscillations of longitudinal waves are in the
same direction that the wave is traveling.

31. 31
Long before Young’s experiment an unexplained phenomena of light was
discovered by a Danish mathematician, Erasmus Bartholin. In 1669 he wrote a
paper describing the double image observed when looking at objects through a
crystal material called Iceland spar. It is now known as calcium carbonate, or
calcite and is a very common mineral. He reasoned that there must be two kinds
of light that take different refractive paths through this material. His was the first
recorded description of a light polarization effect. Materials that exhibit this
“double refraction” became known as birefringent. Incidentally, calcite was the
critical material in the birth of crystal science. In 1801, French scientist Rene-
Just Hauy dropped a piece and was bewildered when he observed that all the
broken pieces had the same shape as the piece before it was dropped. This led
him to study other crystals and later that same year he published a book
describing the six basic crystal forms, founding the science of crystallography.
Depictionsof Thom as Young’s double slit
experim ent
ThomasYoung1773- 1829
Erasmus Bartholin (1625 – 1698) was the first to
describe birefringence, a light polarization effect

32. 32
Over the next 150 years other discoveries about polarized light were made. In
1808, French physicist and mathematician Etienne Louis Malus, while looking
through Iceland spar at the setting sun reflected from the palace window across
from his apartment, noticed that there was only one image, instead of two. As he
rotated the crystal he could vary the intensity of the reflected image. He realized
that the sun’s light reflected from the window was polarized. The orientation of
the crystal that allowed the most light through was at an angle that was rotated
90 degrees from the orientation that allowed the least light through. Through
careful experimentation Malus derived the law that predicts the intensity of light
transmitted through the crystal at any angle between those yielding the
maximum and minimum transmission, aptly called the law of Malus.
In 1812, British scientist, David Brewster, following Malus’ work, found that light
reflected at any angle, other than perpendicular (normal) to the reflecting
surface, is partially polarized. At a certain angle of incidence the reflected light
was completely polarized. This became known as the polarizing angle (also called
the Brewster angle) and is related to the materials refractive index. At this angle,
the incident and refracted rays are at right angles to each other.
Law of Malus: I = I(0) • cos2(q)
Describes the extinction oflight
between polarizers with their
polarizing axes at angle θ
Etienne-Louis Malus (1775 – 1812)
Sir David Brewster (1781 –1868)
θB = ARCTAN (n2 / n1)
θB = ARCTAN (n2 / n1)

33. 33
The same year another French physicist, Francois Arago was the first to produce
a linear polarizer using a stack of glass plates. He also discovered that when
polarized light is passed through a quartz crystal the plane of polarization is
rotated. The longer the path length through the quartz crystal, the more rotation
occurred.
Although Newton’s theory of light particles was still the prevailing belief about
the nature of light among physicists of the time, it could not explain any of these
polarization phenomena. Neither could Huygen’s or Hooke’s pulse waves.
Neither could Young’s longitudinal waves.
Augustin Jean Fresnel was a French engineer working for the department of
bridges and roadways. In his spare time he was also a first-class mathematician
and experimentalist. Using Huygen’s principle of wavelets and building on
Young’s work, through meticulous measurements, he derived mathematic
expressions that precisely predict the interference fringes resulting from
diffraction through the double slits. His formulas included the influence of the
slit size, the slit spacing and distance from the slits to the viewing screen. Using
his math and Young’s setup, the wavelengths of light could now be measured.
Working with Arago, Fresnel showed that two beams that are polarized at right
angles to each other do not interfere and that all the polarization effects observed
can be explained if one considers that light waves are transverse, rather than
longitudinal. This means that they oscillate in directions that are at right angles
to the direction the light ray is travelling. Transverse waves allow an infinite
number of possible planes of polarization. Fresnel then went on to derive
mathematics that describe how the amount of light that is reflected from a
surface depends on the angle of incidence as well as the orientation of its
polarization. This explained the observations of Malus and Brewster. When
Fresnel published his findings they were met with much skepticism, after all, who
is this Frenchmen to challenge the ideas of the great Newton? Another brilliant
mathematician Simeon Poisson, pointed out that Fresnel’s equation predicted a
small bright spot at the center of a shadow cast by an opaque circular disc, and,
how silly is that? Aragothen proceeded to perform the experiment and did find
François Jean Dominique
Arago (1786 – 1853)

34. 34
the “impossible” spot, now known as Poisson’s spot. As more physicists studied
Fresnel’s mathematics and repeated his experiments it became increasingly
obvious that his wave theory of light was correct and able to explain all of the
observed phenomena.
Leon Foucalt, another French physicist, dealt the final death blow to particle
theory by accurately measuring the speed of light in water. In 1676 Ole Roemer
first measured light’s speed astronomically. By 1850, Foucalt and Armand Fizeau
(yet another Frenchman), had each constructed an apparatus that could measure
the speed of light terrestrially. The results obtained were very close to today’s
accepted value. Foucalt’s measurement of light in water showed that its speed
was about 1.333 times slower than what he measured in air. Newton’s particle
theory of light (as well as Descartes’ law of refraction) required that light travels
faster in a refracting material than it does in air. Although Descartes’ law of
refraction was based on two fundamental misconceptions (light travels faster in
water than air, and that it’s speed only changes in the direction perpendicular to
the surface) it did relate the amount of refraction to the ratios of the speed of
light, which turns out to be the case, only inverted. Thus we can now say that the
refractive index of water is approximately 1.333, and can define any material’s
refractive index as the speed of light in a vacuum divided by the speed of light in
the material. Of course, the speed of light in the material, hence its refractive
index, depends on the wavelength of light. Inside the material, red wavelengths
travel faster than blue wavelengths and so the refractive index of the material is
less for red than it is for blue. That means that the change in direction of red
light is less than that of blue light as previously demonstrated by Newton.
By 1850 there wasn’t a physicist alive who didn’t believe in light waves.
Augustin-Jean Fresnel 1788 - 1827
Fresnel reflection curves

35. 35
Industrial age
During the 18th and 19th centuries machines were being invented to perform tasks
that were previously accomplished by animal and human muscles. It began in
the United Kingdom and Europe and soon spread to America and the rest of the
world. Agricultural machines made it easier for farmers to grow more. Machine-
driven textile mills made it easier to produce more cloth. Steam engines were
being used to power trains, ships and factories. This era is called the industrial
revolution and it paved the way for unprecedented productivity and trade
resulting in the largest increase in socioeconomic growth the world had ever seen.
It was during this time that electricity went from a scientific curiosity to a subject
of intense scientific scrutiny. In 1821, Danish physicist and chemist Hans
Christian Oersted, experimenting with an electric battery, accidentally discovered
that when electricity is passed through a wire, a magnetic field is created.
Whenever he would switch his battery on or off the needle of a nearby compass
would momentarily deflect away from true North. This soon led to the invention
of the electric motor by the brilliant British scientist, Michael Faraday. In his
study of magnetic fields, Faraday used tiny bits of iron to visualize magnetic lines
of force. The following sketches depict what he saw:
MEASURING THE SPEED OF LIGHT (C)
Illustration from the 1676 article on
Rømer's measurement of the
speed of light. Rømer compared
the duration of Io's orbits as Earth
moved towards Jupiter (F to G) and
as Earth moved away from Jupiter
(L to K).
C = 220,000,000 M/S
Figure 2: Schematic of
the Fizeau apparatus.
The light passes on
one side of a tooth on
the way out, and the
other side on the way
back, assuming the
cog rotates one tooth
during transit of the
light. (1849)
C = 313,000,000 M/S
Figure 1: Schematic of the Foucault apparatus.Left panel: Light is
reflected by a rotating mirror (left) toward a stationary mirror (top).
Right panel: The reflected light from the stationary mirror bounces
from the rotating mirror that has advanced an angle θ during the
transit of the light. The telescope at an angle 2θ from the source
picks up the reflected beam from the rotating mirror. (1850)
C = 298,000,000 M/S
SPEED OF LIGHT FACTS
C STANDS FOR CELERITAS. IT IS THE
LATIN WORD FOR SPEED.
TODAY’S INTERNATIONALLY ACCEPTED
VALUE IS 299,792,458 METERS PER
SECOND IN A VACUUM.
TODAY’S INTERNATIONALLY ACCEPTED
VALUE FOR 1 METER OF LENGTH IS THE
DISTANCE LIGHT TRAVELS IN A VACUUM
IN 1/299,792,458 SECONDS.
IN ONE SECOND LIGHT CAN TRAVEL
AROUND THE EARTH 23½ TIMES.
IT TAKES LIGHT FROM THE SUN 8 MINUTES
19 SECONDS TO REACH EARTH.
IT TAKES LIGHT FROM THE MOON 1¼
SECONDS TO REACH EARTH.
IN ONE BILLIONTH OF A SECOND LIGHT
TRAVELS ABOUT 11¾ INCHES.

36. 36
Sketch d, in the above figure, shows that when an electric current is passed
through a wire, the magnetic field arranges itself in a circular pattern around the
wire. Here is another depiction.
If the electric current flows in the opposite direction through the wire, the
accompanying magnetic field is set up in the opposite direction. Faraday
investigated this phenomenon and also found that when a magnet is moved near
a closed loop of wire, electricity flows through it, the opposite effect as that

37. 37
observed by Oersted. Faraday observed that if he moved the magnet faster, more
electricity was generated. He also found that electricity could be produced by
moving a wire through the field of an electro-magnet. Faraday used this principle
in 1839 to invent the electric generator.
By the middle of the 19th century the three hottest questions in physics were,
“What is electricity, what is magnetism and how are they related?” Scottish
physicist and mathematician James Clerk Maxwell set out to attempt an answer.
He considered the space that is near electric and magnetic bodies, where the
observed electromagnetic effects are produced, calling it an electromagnetic field
and conceived the following mechanical model for this field:
The dark circles (+) are vortices that spin frictionlessly as current flows through
the wire, depicted by the sawtooth shape. The lighter circles (-) are something
like idler gears that cause all the vortices to spin in the same direction. If the
direction of electric current is reversed, the vortices spin in the opposite
direction.
Maxwell then studied every mathematical analysis known at the time linking
electricity and magnetism and formulated his famous equations to explain the
electromagnetic phenomenon. These are:
The first is based on Faraday’s law describing how a changing magnetic field
generates electricity. The second describes how an electric current generates a
magnetic field. The third describes how an electric field is generated by an
electric charge. And the fourth explains why magnets always have both a north
JamesClerk Maxwell(1831 - 1879

38. 38
pole and a south pole. Tophysicists of the day, these equations spoke volumes.
They unify the electric and magnetic fields in a way that completely describes all
electromagnetic phenomena. Not only that, Maxwell also found that at a certain
speed a changing magnetic field produces a changing electric field which in turn
produces another magnetic field which in turn produces another magnetic field…
each piggy-backing on the other. To his amazement, when he calculated this
speed, he found that it was the speed of light. He immediately deduced that light,
too, is an electromagnetic phenomenon. The sketches below show how
electromagnetic waves can be generated in the electromagnetic field, which, by
now, Maxwell has equated with the ether.
An alternating electric current (one that moves back and forth) in the wire sets up
a dipole (separation of electric charges). Each time current travels down the wire
and back, one sinusoidal wave in the magnetic field is created. This, in turn,
gives rise to one sinusoidal wave in the electric field. The higher the frequency of
the electrical oscillations, the shorter the wavelength of the electromagnetic
radiation that is produced. Maxwell’s essay, A Dynamical Theory of the
Electromagnetic Field was published in 1865 and is still considered mostly
correct.
In 1886, German physicist Heinrich Hertz, after reading Maxwell’s paper, built a
device that demonstrated the existence of electromagnetic waves. When an
electric battery is connected to a circuit containing a small airgap, it does not
simply empty out. It surges back and forth reversing its direction several
thousand to several billions of times per second depending on the strength of the
charge and the distance of the air gap. (We now know that this is also what
happens when lightning strikes). Hertz built two such spark gap circuits. One he
energized with an electric battery (transmitter) while the other was placed at
some distance away (receiver). Hertz observed that at the instant a spark jumped
across the airgap in the transmitter, a weaker spark could be seen to jump the gap
in the receiver. Hertz had created and transmitted radio waves. He was able to
measure the frequency and wavelength of the transmitting waves and found that
they did, indeed, travel at the speed of light. Units of frequency are now called
Hertz, in his honor, and simply mean the number of times per second. For
instance, a radio signal having a frequency of 10 Megahetrz repeats itself 10
million times each second. The AC current that is used in the United States has a
frequency of 60 hertz. Hertz did not realize the potential of his discovery, but the
Italian inventor Guglielmo Marconi did. In 1896 he sent a radio message to
someone three miles away and five years later sent one across the Atlantic.

39. 39
So, light is an electromagnetic wave in the electromagnetic field traveling at c,
nearly 300 million meters per second. The sketch below shows the relationship
between frequency and wavelength for an electromagnetic wave. Only the
electric field component is shown but the same relationship between the speed,
wavelength and frequency is also true of the magnetic field component.
But how can this wave that Hertz produced be called light? After all, you can’t
see it. Invisible light seems to be a contradiction in terms. Actually, invisible
light had been observed and reported nearly 100 years prior to Hertz’s radio
waves.
In 1800, professional musician and amateur astronomer William Herschel was
testing colored glass filters so he could comfortably observe sun spots through his
telescope. When using a red filter he found there was a lot of heat produced.
Herschel discovered infrared radiation by accident. Allowing sunlight to pass
through a prism and using a thermometer he measured the temperature of each
color of the dispersed sunlight. Another thermometer, placed just beyond the red
end of the visible spectrum was meant to measure the ambient air temperature in
the room as a control. Herschel was shocked when it showed a higher
temperature than any of the colors of the visible spectrum.
Heinrich Hertz (1857 – 1894)

40. 40
Further experimentation led to Herschel's conclusion that there must be an
invisible form of light beyond the red portion of visible spectrum. This light
became known as infrared.
Discovered in 1800 by William Herschel
Produced by any matter hotter than absolute zero (-273 degrees
Celsius)
Used in a wide range of applications including heating, remote
temperature
sensing, military targeting, weather forecasting, night vision,
spectroscopy,
climatology, short range communications (remote controllers) and
astronomy.

41. 41
In 1801, Johann Ritter conducted experiments with silver chloride, a chemical
which turns black when exposed to sunlight. It was known that exposure to blue
light caused a greater reaction in silver chloride than exposure to red light. Ritter
decided to measure the rate at which silver chloride reacted when exposed to the
different colors of light. Todo this, he directed sunlight through a glass prism to
create a visible spectrum. He then exposed the silver chloride crystals to each
color of the spectrum. Ritter noticed that the silver chloride showed little change
in the red part of the spectrum, but increasingly darkened toward the violet end
of the spectrum. This proved that exposure to blue light did cause silver chloride
to turn black much faster than exposure to red light. Ritter then placed his silver
chloride crystals in the area just beyond the violet end of the spectrum. To his
amazement, he saw that the silver chloride displayed an intense reaction well
beyond the violet end of the spectrum, where no visible light could be seen. This
showed for the first time that an invisible form of light existed beyond the violet
end of the spectrum. This new type of light, which Ritter called “chemical rays”,
later became known ultraviolet radiation. The chemical reaction of the silver
chloride when exposed to light formed the basis of what was to become
photography.
As discussed earlier, Heinrich Hertz produced radio waves in 1886 in order to
confirm Maxwell’s electromagnetic theory. Soon after, shorter wavelengths were
produced by similar means using hollow metal cavities. These became known as
microwaves and were first demonstrated in 1894 by Chandra Bose.
Discovered in 1801 by Johann Wilhelm Ritter
Produced by many natural and man-made sources
Used in a wide range of applications including fluorescent lighting, pest control,
mineral analysis, astronomy, spectrophotometry, photolithography, tanning,
food processing and sterilization, fire detection, forensics and curing polymers
such as adhesives, inks and coatings

42. 42
In 1895, German physicist Wilhelm Roentgen accidentally discovered an
unknown radiation while experimenting with electrical discharges through
vacuum tubes containing small amounts of different gases. He discovered that
something was causing photographic plates that were nearby tobecome exposed,
even though they were wrapped in black paper and inside the boxes intended to
protect them from exposure to light. He also found that this radiation passed
right through soft tissue, but was reflected by bones when he had his wife place
her hand in front of a photographic plate and exposed it to this radiation.
Roentgen called this radiation Xrays because it was so mysterious.
Demonstrated in 1894 by Jagdish Chandra Bose
Produced by devices such as magnetrons, klystron tubes, and cyclotrons
Detected from all directions of deep space (cosmic microwave background
radiation).
Used for broadcasting, telecommunications, radar, semiconductor
manufacturing processes, astronomical research and, of course, cooking,
Discovered in 1895 by Wilhelm Roentgen
Produced by bombardment of certain metals by accelerated
electrons
Used in diagnostic medical imaging.
Used to treat certain types of cancer.
Used in analytical science (crystallography, microscopy,
fluorescence
spectroscopy, astronomy)
The firstmedical Xrayphotograph

43. 43
Toward the end of the 19th century, Ernest Rutherford and his students
investigated the radioactive emission of uranium and other radioactive elements.
Three types of emission were discovered and were called alpha, beta and gamma
rays. The alpha and beta rays were discovered to be atomic particles (electrons
and protons) that could be steered by a magnetic field. The gamma rays could
not. In 1900, French scientist, Paul Villard, correctly identified gamma rays as
type of high energy electromagnetic radiation.
Discovered in 1900 by Paul Ulrich Villard
Produced by radioactive elements and by nuclear
explosions.
Used in medicine to treat cancer, perform diagnoses and
to sterilize
medical equipment
Used to kill bacteria in food products
Used in port security to scan ship containers

44. 44
All these forms of electromagnetic radiation, along with visible light, form the
electromagnetic spectrum. They all exhibit both the ray and wave properties of
light and differ only in wavelength. Of course, the way that these interact with
matter can be dramatically different depending on the properties of the matter.
Wavelength is simply a distance like a micron, an inch, or a mile. For visible light
this is a very short distance, spanning the range of about 400 nanometers for
blue light to 700 nanometers for red. 700 nanometers is the same distance as
0.0007 millimeters or 0.00003 inches. For UV, X-rays and gamma radiation it’s
even shorter but for infrared and microwave radiation the wavelength is longer.
For radio signals the wavelengths range from 0.1 to 1000 meters. (That’s over a
half mile, not bad for one wave!).
The following illustration shows the size of light wavelengths compared to objects
that are more familiar to everyday experience. (Unlike the previous chart, this
one is showing the wavelengths in decreasing length from left to right).
THE ELECTRO-MAGNETIC SPECTRUM

45. 45
Wave optics phenomena
INTERFERENCE
Have you ever wondered why soap bubbles are colored, or why an oil spill on a
wet road has colors in it? This is what happens when light waves pass through a
very thin layer with two reflective surfaces. When white light, which is a mixture
of different wavelengths, shines on the film some of the light reflects from the top
surface and some of it passes through the film and is reflected from the bottom
surface. Because the waves that penetrate the film have passed through the film’s
thickness and back, they become out of sync with the waves reflected by the top
surface. Physicists refer to this state as being out of phase. Interference occurs
and the intensity of the waves either adds together or subtracts from each other
depending on the phase relationship between the twointerfering waves. The
thickness of the film determines which wavelengths (colors) have undergone the
amount of phase shift required to meet conditions for constructive or destructive
interference. The wavelengths that undergo constructive interference are the
colors that you see. If you shift your angle of view of the soap bubble film you will
see a different color since you have changed the amount of film thickness
between the reflected waves of the two surfaces traveling to your eyes. As the
wall of the bubble becomes thinner it changes color to red, then orange, then
yellow, then green, then blue and and then violet. As it continues to thin out
beyond this it has become too thin to constructively interfere even the shortest
wavelengths of visible light. It momentarily turns a dark gray and then, pop.
Thin film of air between slides produces
an interference pattern.
Interference in soap bubbles

46. 46
Optical coatings
Interference of light waves in thin films is the principle that makes optical
coatings work. By using coating materials of differing refractive index thin films
can be applied to an optical surface to control the amount of light of particular
wavelengths that reflect from the surface or transmit through it. By carefully
controlling the layer thicknesses coatings that reflect virtually no light, to those
that reflect virtually all the light, and anywhere in between, for given
wavelengths, can be achieved. Coatings that reflect short wavelengths and
transmit longer wavelengths, or vice-versa are called dichroic coatings. These
require many layers, sometimes more than 100. Many coating designs use only
two coating materials, one of high index and one of low index, that are deposited
in alternating layers.
For wav es undergoing constructiv e
interference, the amplitude,or height, of
the waves are added.This happens when
the two wavesare in phase,that is, if the
crests and troughsof the wav es coincide
with each other.
For wav es undergoing destructiv e
interference, the two wav es cancel each
other out.This happenswhen the wav es
are outof phase,thatis,whenthe crestsof
one wave coincide withthe troughsof the
other.
The window on the right has been antireflection coated. The one on the left has not.

47. 47
Used in optical metrology
Light interference is used to evaluate optical surfaces and distortion imparted to
light as it passes through one or more optical components. In the case of surface
metrology, reference surfaces can be used to see the departure of the surface
being tested, from the ideal shape. These are called test-plates and are made to a
specified surface geometry (radius and irregularity) within very tight tolerances.
For example, if you want to test a convex lens surface to confirm that it meets
requirements for radius of curvature and irregularity (that is, that every point on
the surface is in the sphere defined by that radius), you can use a concave test
plate made to the exact radius. By placing the concave surface of the test-plate in
contact with the convex surface being tested interference fringes are created.
These are significantly more visible using monochromatic light than they are
using white light. If the interference fringes are straight and equally spaced then
the convex surface that you are testing matches the radius and regularity of the
concave reference surface. Any deviation of the fringes from straight and equally
spaced represents a departure of the convex surface from ideal. If the fringes
bend in such a way that they are arcs of circles, then the radius is slightly off. If
the fringes describe one or more concentric circular rings (bulls-eye pattern) then
the radius is farther from ideal. One can easily determine whether the surface is
convex or concave, relative tothe reference surface, and make the necessary
correction by adjusting the polishing stroke. Any deviation, other than those
described, is surface irregularity. This is a localized departure from an ideal
surface. What’s actually being measured is the variation in thickness of the thin
air gap between the twosurfaces. The fringes are a result of light reflected by the
optical surfaces on either side of the air gap. Wherever the depart changes by one
half of a wavelength of the light being used, one fringe is created. Test-plates can
be made to test concave and flat as well as aspheric surfaces. Some drawbacks of
test-plates is that you need one for each different radius of curvature that you
wish to test and that quantitative assessment of the surface is done manually and
requires some experience.
Interferometers, utilizing a laser source, are used for the same purposes as test-
plates but offer some distinct advantages. When equipped with a radial slide, a
wide range of both convex and concave radii can be measured using a single
reference sphere. Computer software, written to assess the interference pattern
is considerably more accurate than what can be determined using test-plates.
Interferometers are alsoable to measure transmitted wavefront (TWF)
distortion. That is a measure of how a nearly perfect light wavefront is distorted
by one or more components, and, for transmissive optics is of more importance
than surface deviations. TWF measurement is not possible with test-plates.
Interference
fringes seen
using a test
plate
Interference
fringes seen
using a laser
interferometer

48. 48
Diffraction
Diffraction is the slight bending of lightwaves (sound waves and water waves too,
actually) around small obstacles as well as the spreading out of the waves past
small openings. In order for the effect to be observed the obstacle or opening has
to be comparable in size to the wavelength of the light. The amount of bending
depends not only on the size of the obstacle or opening, but also on the
wavelength of light. By virtue of the slight change in direction of the light waves,
a shift in phase between adjoining waves causes constructive and destructive
interference to occur. This results in discrete orders of diffraction, labeled m=0,
m=1, etc. in the sketch on the left below. These patterns apply to diffraction for
light of a single wavelength (monochromatic).
be
For white light undergoing diffraction, each of these orders, except the m=0
order, will contain a spread of color with violet nearest the m=0 order and red the
T he colors seen in spider webs and compact discs are due to diffraction

49. 49
farthest from it. The reason that violet is nearest is because its wavelength is the
shortest (among visible light) and so it encounters the condition for constructive
interference sooner.
Diffraction also occurs when waves encounter a small obstacle, or a very narrow
one, such as a hair or thin wire or even a thin scratch or groove on a surface.
Several qualitative observations can be made of diffraction in general:
 The angular spacing of the features in the diffraction pattern is inversely
proportional to the dimensions of the object causing the diffraction, in
other words: the smaller the diffracting slits or obstacles the 'wider' the
resulting diffraction pattern and vice versa.
 The diffraction angles do not vary if there are more or less diffracting
objects involved, (for instance, 2, 100, 1000, etc slits or grooves) they
depend only on the ratio of the wavelength to the size of the diffracting
object.
 When the diffracting object has a periodic structure, for example with
many slits or grooves of the same width and the same distance apart, the
diffracted pattern features become sharper.
In order to efficiently separate (disperse) white or other mixed-wavelength light
into its component wavelengths by diffractive methods a component containing
many very thin grooves, called a diffraction grating, is used. The spacing between
the grooves is typically on the order of light wavelengths. Diffraction gratings are
usually rated by the number of grooves per millimeter (spatial frequency). One
having a higher spatial frequency will result in diffracted orders at wider angles
and with more of the incident light diffracted into these orders (diffraction
efficiency) than one having a lower spatial frequency. Diffraction gratings have
replaced dispersing prisms in instruments such as monochromaters and
spectrometers. The first diffraction grating was made around 1785 by
Philadelphia inventor David Rittenhouse, who strung hairs between two finely
threaded screws. German physicist Joseph von Fraunhofer's, using the same
principle, made a wire diffraction grating in 1821. Today gratings are made by
mechanically ruling the grooves or by holographic techniques (photographs of
laser light interference fringe patterns). Diffraction gratings can be made that
work in either transmission or reflection.
Green laser lightthrough a
transmission grating
White lightdispersed by a large
transm ission grating
White light dispersed by a
reflection grating

50. 50
Examples of diffraction in everyday life
The effects of diffraction can be readily seen in everyday life. The closely spaced
tracks on a CD or DVD act as a diffraction grating to form the familiar rainbow
pattern we see when looking at a disk. This principle can be extended to engineer
a grating with a structure that can produce any diffraction pattern desired like the
hologram on a credit card for example. Diffraction in the atmosphere by small
particles can cause a bright ring to be visible around a light source like the sun or
the moon. The shadow of a solid object, produced by light from a point source,
shows small fringes near its edges. All these effects are a consequence of the fact
that light is a wave.
Diffraction can occur with any kind of wave. Ocean waves diffract around jetties
and other obstacles. Sound waves can diffract around objects, this is the reason
we can still hear someone calling us even if we are hiding behind a tree.
Diffraction can also be a concern in imaging applications as it sets a fundamental
limit to the resolution of a camera, telescope, or microscope. This is called the
diffraction limit.
Polarization
Light waves are transverse electromagnetic radiation comprised of an electric
field vibration (snakelike wiggle) and a magnetic field vibration. A transverse
wave is one that vibrates in a direction that is at a right angle to the direction in
which the wave is traveling. Other transverse waves include the waves on the
surface of water, the motion of a plucked string of a musical instrument and an
audience wave at a sporting event. This is quite different from a sound wave or a
Two images seenthrough a birefringent
crystal resultfrom the dependence of the
m aterial’s refractiv e index on the
polarization orientation of the light
passing through.
Stress birefringence
in a plastic cup

51. 51
seismic wave from an earthquake in which matter vibrates (bounces back and
forth) in the same direction as the wave is traveling. These kinds of waves are
called longitudinal or compressive. In order to model, understand and predict
transverse light waves it is only necessary to consider the behavior of the electric
field vibration since the magnetic field vibration will always be in phase and at a
right angle to it.
Light emitted by the sun, a lamp or a candle flame is unpolarized. Such light
waves are created by electric charges that vibrate in a variety of directions, thus
creating an electromagnetic wave that vibrates in a variety of directions. The
concept of unpolarized light is rather difficult to visualize. It is helpful to picture
unpolarized light as a wave that has an average of half of its vibrations in a
horizontal plane and the other half in a vertical plane.
Linearly polarizedlight
Light having its electric field vibrations confined to a single plane of propagation
is described as linearly polarized.
There are a number of ways tocreate linearly polarized light from unpolarized
light:
Longitudinal sound wav es
produced by a tuning fork
Transv erse wav es can
oscillate in a horizontal
plane,a vertical plane or
any where in between
Head-on v iew of
approaching
unpolarized light
wav es
Two examples of a linearly
polarized lightwave. The
wave on top ispolarized in
the horizontal plane of
propagation and the one
on bottom in a v ertical
plane of propagation.

52. 52
By transmission through a polaroid filter
The most common method of polarization involves the use of a Polaroid filter.
Polaroid filters are made of a special material that is capable of blocking one of
the two planes of vibration of an electromagnetic wave. (Remember, the notion
of two planes or directions of vibration is merely a simplification that helps us to
visualize the wavelike nature of the electromagnetic wave.) In this sense, a
Polaroid serves as a device that filters out one-half of the vibrations upon
transmission of the light through the filter. When unpolarized light is
transmitted through a Polaroid filter, it emerges with one-half the intensity and
with its vibrations in a single plane; it emerges as linearly polarized light.
A Polaroid filter is able to polarize light because of the chemical composition of
the filter material. The filter contains long-chain molecules (iodine compounds
are normally used for visible light) that are aligned within the filter in the same
direction. During the fabrication of the filter, the long-chain molecules are
stretched in one direction. As unpolarized light strikes the filter, the portion of
the waves vibrating in the stretched direction are absorbed by the filter.
The alignment of these molecules gives the filter a polarization axis. This
polarization axis extends across the length of the filter and only allows vibrations
of the electromagnetic wave that are parallel to the axis to pass through. Any
vibrations that are perpendicular to the polarization axis are blocked by the filter.
Thus, a Polaroid filter with its long-chain molecules aligned horizontally will have
a polarization axis aligned vertically. Such a filter will block all horizontal
vibrations and allow the vertical vibrations to be transmitted (see diagram
above). On the other hand, a Polaroid filter with its long-chain molecules aligned
vertically will have a polarization axis aligned horizontally; this filter will block all
vertical vibrations and allow the horizontal vibrations to be transmitted. Polaroid
filter material was invented in 1929 by Edwin H. Land.

53. 53
By reflection from a non-metal surface at Brewster’s angle
Light reflected from a non-metal surface at Brewster’s angle is completely linearly
polarized. The plane of polarization is the plane that is at a right angle to the
plane of incidence (the plane containing the incident, refracted and reflected
rays). By definition, this is called the S-plane. The plane that is parallel to the
plane of incidence is called the P-plane. At Brewster’s angle the P-plane
component of the incident light is refracted normally, according to the refractive
index of the material, and is at an angle of 90 degrees to the reflected ray. The
refracted ray is partially polarized.
By transmission through a Brewster stack
As previously mentioned, at Brewster’ s angle the refracted ray emerges partially
polarized. By adding more dielectric (electrically non-conductive) surfaces
positioned at Brewster’s angle to the refracted ray successively more S-plane
polarized light is removed resulting in transmitted light that is linearly polarized
in the P-plane.
θB = ARCTAN (n2 / n1)
Linear polarization in
transm ission can also be
achieved at Brewster’sangle by
usingthin film s of dielectric
coatingmaterial deposited on a
substrate,instead of m ultiple
elem ents.

54. 54
By transmission and reflection through a birefringent crystal
Materials like crystalline quartz and calcite are birefringent. This means that
their refractive index depends on the polarization orientation of the light that
passes through them. Light that is polarized in one specific orientation,
depending on the crystal type and how it is cut in relation to its crystal axis, will
refract according to the normal law of refraction, that is, the refracted ray will be
in the same plane as the incident and reflected ray (plane of incidence). This is
called the ordinary ray and the index for that polarization orientation is denoted
as no. Light that is polarized in a plane 90 degrees to that undergoing ordinary
refraction will be refracted at a different angle and not in the plane of incidence
as is the ordinary ray. This is called the extraordinary ray and is denoted as ne.
The birefringence of a material is defined as no - ne.
Crossed and uncrossed polarizers
Light passing through two linear polarizers, positioned in series, can be adjusted
in intensity between a maximum and minimum value by rotating the second
polarizer. In this arrangement, the first polarizer is normally not adjusted and
establishes a plane of polarization. This is typically called the polarizer. If the
second polarizer, called the analyzer, is rotated such that its polarization axis is
parallel to the plane of polarization established by the polarizer (uncrossed), as in
the top arrangement of the following sketch, the amount of light transmitted by
the analyzer is a maximum. If the analyzer is rotated 90 degrees such that its
polarization axis is perpendicular to the plane of polarization established by the
polarizer (crossed), the light transmitted through the analyzer is a minimum.
The light is said to be extinguished. This is shown by the bottom arrangement of
the sketch. For any rotation angle of the analyzer in between these positions, the
relative intensity of light transmitted through the analyzer is given the Law of
Malus: I = I(0) • cos2(q) Where:
I is the intensity of the transmitted light
I(o) is the intensity of light incident on the analyzer, and
Q is the angle that the analyzer is rotated to (relative to the uncrossed 0 degree
position)
Glan-Thom pson prism
polarizer
Wollaston prism polarizer

55. 55
The ratio Imax / I min is called the extinction ratio. Such a setup can be used to
measure small amounts of birefringence that may be present, but not desired, in
optical components and systems. This is called stress birefringence or residual
birefringence and, in glass optical materials is the result of limitations in the
annealing process. Used in this fashion, the light source is typically a laser.
This type of system can also be used to visually analyze transparent materials for
localized stress birefringence. In this context it is called a polariscope. Using a
white light source the sample to be analyzed is placed in between the crossed
polarizer and analyzer. During manufacturing, when plastic solidifies, internal
stresses are set up in the material. This stress results in non-uniform
birefringence. The various colors seen in the following image of a plastic
protractor correspond to the amount of localized stress in the plastic material and
result from the fact that light of different wavelengths undergo a proportionally
different phase relationship between the refracted ordinary (o) and extraordinary
(e) rays.

56. 56
Wavelengths of visible light are typically described in units of nanometers (1
nanometer = 1 X 10-9 meters= one one billionth of a meter). Likewise, the phase
difference between the ordinary and extraordinary rays can be described in
nanometers. If the thickness of the sample is known, the Michel-Levy chart,
shown below, can be used to quantify the stress birefringence based on the colors
seen.
Birefringence chart originally developed by Frenchgeologist Auguste
Michel-Lev y to identify v arious m inerals

57. 57
Phase retardation -Waveplates
A waveplate works by shifting the phase between two perpendicular polarization
components of a light wave. A typical wave plate is a birefringent crystal with a
carefully chosen orientation and thickness. The crystal is cut so that the optic
axis is parallel to the surfaces of the plate. Light polarized along this axis travels
through the crystal at a different speed than light with the perpendicular
polarization, creating a phase difference. When the extraordinary index is larger
than the ordinary index, as in crystal quartz, the extraordinary axis is called the
"slow axis" and the perpendicular direction in the plane of the surfaces is called
the "fast axis".
Depending on the thickness of the waveplate, light with polarization components
along both axes will emerge with a changed polarization state. A wave plate is
characterized by the amount of retardance (R) that it imparts to the two
polarization components, which is related to the birefringence Δn and the
thickness T of the crystal by the formula R = 2π Δn T / λ.
Waveplates, also called phase plates or retardation plates, are used to effect
polarization changes to light that is already polarized. A quarter waveplate is
made to a precise thickness so that it will effect a phase difference of one fourth of
a wavelength between the ordinary and extraordinary rays. If linearly polarized
light is incident on a quarter waveplate, and the plane of polarization of the
incident light is at 45 degrees from either the fast or slow axis (halfway in
between) of the waveplate, the light transmitted through the waveplate is said to
be circularly polarized. For every wavelength of distance that circularly polarized
light travels, the plane of polarization rotates 360 degrees. At any location along
its propagation axis the intensity of light is equal in any plane of polarization.
This is because the component waves, at right angles to each other, are equal in
amplitude and 90 degrees (hence one quarter wave, since 1 wave is 360 degrees)
out of phase with each other. Similarly, circularly polarized light can be
converted to linearly polarized light.
A half waveplate is made to effect a half wavelength of phase difference between
the ordinary and extraordinary rays. It can be used to rotate the plane of
polarization of incident linearly polarized light to any desired plane. Although
quarter and half waveplates are most commonly used, it is possible to make a
waveplate that will effect a phase retardance of any value. These are sometimes
used to correct the phase difference between P and S-plane radiation that has
been incurred as a result of total internal reflection.
Waveplates are used in laser systems for polarization control, Q-switching and
opto-isolation and in specialized analytical microscopes.

58. 58
Elliptically polarized light contains unequal wave components. This is the result
of one or both of the following conditions: 1) the ordinary and extraordinary rays
are out of phase by some amount that is not an integer multiple of one fourth of a
wavelength (or 90 degrees) 2) the ordinary and extraordinary rays are not
equal in intensity. The polarization direction of elliptically polarized light also
rotates 360 degrees for every wavelength of distance traveled, however, the
intensity of the combined waves varies from a maximum to a minimum for each
wavelength of distance traveled.
A quarter waveplate converts linearly
polarized lighttocircularly polarized light
A half waveplate allowslinearly polarized
light to be rotated to any plane of
polarization
The top sketch shows thattwo wavesthatare out of
phase by one half of a wavelengthadd togetherto
resultin a wave thatislinearly polarized.
Two wavesthatare equal in amplitude and outof
phase by one quarterof a wavelengthadd together to
resultin a wave thatrotates asthe wave travelsand
hasa uniform intensity inany plane perpendicularto
itsdirection of travel. This is called circular
polarization.
Two wavesthatare eitherunequal in intensity and/or
out of phase by an amountthatisnot a multiple of one
quarter of a wavelengthadd togetherto resultin a
wave that iscalled elliptically polarized. Asthis wave
propagatesit rotatesand its intensity variesfrom a
m aximum to a minimum value for every wavelength
of distance traveled

59. 59
Polarization rotation
The rotation of the orientation of linearly polarized light was first observed in
1811 in quartz by French physicist François Jean Dominique Arago. Around this
same time, Jean Baptiste Biot also observed the effect in liquids and gases of
organic substances such as turpentine. In 1845, Michael Faraday discovered that
certain glass and crystal materials, in the presence of a magnetic field, rotate
linearly polarized light. Materials that exhibit polarization rotation are called
optically active.
A crystal quartz window, if made such that the crystal axis is perpendicular to the
polished surfaces, (the opposite direction as a crystal quartz waveplate) is a
polarization rotator. By carefully controlling the thickness the amount of rotation
undergone by a linearly polarized incident wave, can be controlled to an exact
amount. This type of rotator has many useful applications in laser technology.
The phenomenon of polarization rotation is also employed in LCD display
technology. LCD televisions and monitors produce the image you see by blocking
or transmitting the light from a backlight using liquid crystals sandwiched in
between two glass plates. This is the same basic principle used in the liquid
crystal displays found in everyday items such as digital watches and instrument
readouts.
Rotation of linearly polarized light as it
passes through an optically active
material

60. 60
An LCD is made up of a thin layer of liquid crystals arranged in a matrix (or grid)
of a million or more pixels (picture elements), which are themselves made up of
three sub-pixels aligned to a color filter for each of the primary colors; red, green
and blue. This layer is sandwiched between the two glass plates, which are
covered in a matrix of electrodes and transistors (electronic switches), each
coated with a polarizing filter. The twopolarizing layers only allow light vibrating
in one direction to pass through them, one allows horizontally polarized light
through and the other passes vertically polarized light.
The light source in an LCD is its backlight so this unpolarized light becomes
vertically polarized as it passes through the first polarizing filter at the back of the
display. The other polarizing layer on the front sheet of glass is horizontally
polarized, so ordinarily the now vertically polarized light coming from backlight
can't pass through it. The role of the liquid crystal layer in the middle of the
display is to rotate the vertically polarized light travelling through it by so it can
pass through the front, horizontally polarized filter. By varying the voltage
applied to the liquid crystal sub-pixels the amount of polarization rotation of the
light can be controlled, allowing more or less light of each color through.
Individual pixel colors are produced by the combination of the primary colors
produced by each sub pixel. The pixel's overall brightness is produced by the
sub-pixels relative intensities. Many thousands of these pixel units operating
together in the display combine to produce the picture image you see.
Polarization in nature
Human eyes are not capable of directly discerning any differences between
polarized and unpolarized light, although the effects are all around us. Gas and
water molecules in the atmosphere scatter light from the sun in all directions, an
effect that is responsible for blue skies, white clouds, red sunsets, and a
phenomenon termed atmospheric polarization. The amount of light scattered
depends upon the size of the molecules (nitrogen, hydrogen, oxygen, water) and
the wavelength of light, as demonstrated by Lord Rayleigh in 1871. Longer

61. 61
wavelengths, such as red, orange, and yellow, are not scattered as effectively as
are the shorter wavelengths, such as violet and blue.
Atmospheric polarization is a direct result of the scattering of sunlight by gas
molecules in the atmosphere. The unpolarized sunlight is scattered at right
angles to the direction of its propagation, and is polarized either vertically or
horizontally, depending upon the direction of scatter. A majority of the polarized
light impacting the Earth is polarized horizontally (over 50 percent). For this
reason, polarizing filters are also quite useful in outdoor photography. These can
be attached to the front of a camera lens to reduce glare and increase overall
image contrast in photographs

62. 62
Sunlight reflected from horizontal surfaces, such as the highway, car windshields
or water, is partially polarized in a direction that is parallel to the ground. (It is
completely polarized at Brewster’s angle). This light can be blocked by polarizing
filters oriented in a vertical direction as with a pair of polarized sunglasses. The
lenses of the sunglasses have polarizing filters that are oriented vertically with
respect to the frames and make driving or boating in bright sunlight safer.

63. 63
Looking for the ether
Since Christian Huygens first formalized his wave theory of light in 1690 up to
the electromagnetic wave equations of Maxwell and subsequent experimental
proof by Hertz in 1887, proponents of light waves found it necessary tosuppose
that there was some type of medium through which light waves could travel.
After all, a wave is only an influence that causes actual matter tomove. In the
case of sound waves, it is air that does the moving. The matter that was put into
motion by light waves became known as the luminiferous ether, and it has to
have some remarkable properties. It has to exist everywherethat light can travel,
including the vacuum of space, the atmosphere surrounding the earth and inside
of transparent media like water and glass. It also has to be rigid, like a solid, in
order to support a transverse wave oscillating through light years of space and
vibrating millions, billions and even trillions of times per second. At the same
time it has to be so tenuous that the sun, earth and planets can travel through it
without ever slowing down. Since everything in the known universe is moving,
physicists were very interested in the ether, since it would be the only thing that
is at rest, and the motion of all matter can be described in reference to it.
In 1881, American physicist Albert Michelson attempted an experiment to detect
the earth’s motion within the ether. His reasoning was that, if the earth moved
through a stationary ether, then a light beam that was traveling in the direction
that the earth moved and back would take slightly less time to make the round
trip than a light beam traveling perpendicular to the direction of the earth’s
motion and back.
Using a light interferometer that he invented, Michelson attempted to perform
the experiment but was unable to get meaningful results due to the effects of
mechanical vibrations, from the city streets, on his interferometer. In 1887, with
the assistance of his colleague at the Case School of Applied Science, Edward
Morley, Michelson tried again. Tonegate the effects of vibration, the
interferometer was built in a basement laboratory on a twoton sandstone slab
that was five feet square and a foot thick. The slab sat on a ring-shaped wooden
support that floated on a pool of mercury. The interferometer consisted of a
monochromatic (single color) light source, a partially mirrored beamsplitter,
which divided the beam into perpendicular paths, and two mirrors, one to return
The motion of the earth relative
tothe stationary ethercan be
viewed as an etherwind. A light
beam travelingin the same
direction as the etherwind will
take a slightly longer path than
one traveling perpendicular toit.

64. 64
each of the beam paths back through the beamsplitter and on to a viewing screen.
It was essentially a race between the two light beams. Any difference in the path
length between the two beams could be observed in the form of interference
fringes. Using the accepted velocity of the earth in orbit around the sun,
Michelson calculated the difference in path length between the twobeams to be
about one tenth of a fringe. This difference should have been easily seen with the
improved interferometer, but, after five days of taking measurements in every
direction, no difference in beam path could be seen.
Several explanations were provided to explain the null result. One suggestion
was that the earth actually “dragged’ a little bit of ether with it as it moved. (This
had been previously suggested by Augustin Fresnel, nearly eighty years earlier, to
explain why no evidence of the ether could be observed.) Another, suggested
independently by twophysicists, George Fitzgerald and Hendrick Lorentz, was
that distance and matter, including all measuring equipment, shrinks in the
direction of the ether. Therefore, although there was the expected path
difference, due to the ether wind, it could not be seen because the effect of the
ether wind on the measuring equipment was to shrink it by exactly the amount
necessary tocompensate for the difference. This became known as Fitgerald-
Lorentz contraction. Belief in the ether was so strong that many scientists were
in denial of the experimental results.
Michelson, himself could not accept the results and continued the measurement
under various conditions for the next forty-four years. Until his death, in 1931,
Michelson would not believe that there could be a wave without some material
substance to do the waving.

65. 65
Spectroscopy
In 1802, William Wollaston reported the existence of dark lines in the spectrum
of sunlight. He passed sunlight through a very narrow slit (no more than 1 mm)
so that it fell on a prism. Projecting the light over a distance of 10-12 feet,
Wollaston saw the familiar continuous solar spectrum. He also observed seven
dark lines at various locations in the otherwise continuous spectrum. (The
modern term for what Wollaston saw is an absorption spectrum).
Twelve years later, a young optician named Joseph von Fraunhofer was looking
for ways to check dispersion in the glass that he used to build high quality
telescopes. Using much better instruments, Fraunhofer mapped out 574 thin
black lines that he observed in the sun's spectrum.
Eight of the most prominent lines he labeled A to G. The D-line, in the yellow
part of the spectrum was actually two closely-spaced lines that Fraunhofer called
D1 and D2 . Today, these lines are known as the Fraunhofer lines. Here is what he
drew:
Fraunhofer had previously observed bright yellow lines in the spectrum of
various flames appearing in the same position as the sun’s dark D-lines.
He found that the spectrum of the moon and planets contained the same lines as
that of the sun. This is no surprise, since these bodies only reflect sunlight. He
also found that the spectrum of stars often contain some different lines and some
of the same dark lines as the sun. Fraunhofer reported the results of his research.

66. 66
In 1821, Fraunhofer used a diffraction grating to measure the wavelengths of the
two D lines, obtaining values very close to the modern ones (589.592nm and
588.995nm), but could not explain why they were there.
Other experimenters, including John Herschel (son of William Herschel, the
discoverer of infrared light) and David Brewster began looking at various spectra.
Herschel studied the bright lines seen through a prism when chemical substances
are heated by a flame. (These later became known as emission lines and are the
spectrum of light produced by the specific gases formed by the heat of the flame).
David Brewster found dark lines in the spectrum of light passed through cool
gases. (These lines are absorbed from an otherwise continuous spectrum by the
gas and are the same wavelengths as the emission lines for a specific gas). From
his research he concluded that the dark lines of the solar spectrum resulted from
the absorption of certain colors of sunlight by the gases that exist near the sun’s
surface.
In 1859, two Germans, physicist Gustav Kirchhoff and chemist Robert Bunsen (of
Bunsen burner fame) began a systematic study of the known chemical elements
using a spectroscope designed specifically for this purpose. Within a year they
announced that elements can positively be identified by their unique spectra.
In this manner they identified many of the elements contained in the sun’s
atmosphere based on the dark lines in the solar spectrum. The yellow pair of
Fraunhofer lines were found to be characteristic of the metal sodium. Detection
of unknown emission lines led to Bunsen’s later discovery of the elements
caesium and rubidium. (He named these elements using the Latin words for
“deep blue” and “dark red” respectively because of the location of their emission
lines). Kirchhoff and Bunsen found that any metal always exhibits the same
emission spectrum regardless of the chemical compound that it is found in. They
also discovered that the colored lines emitted by a heated gas (emission
spectrum) were the same lines that were absorbed by the gas (absorption
Gustav Kirchhoff and
Robert Bunsen
Spectroscope of Kirchhoff and
Bunsen

67. 67
spectrum). Although scientists could use emission and absorption spectra to
identify unknown elements, they could not explain what caused them or why
each element has a unique spectrum. It would be another 50 years before this
began to be understood.
Light is energy
Toward the end of the 19th century most of the observed phenomena of light
could be explained in the context of the wave model of light. Visible light was
understood to be a small part of a larger phenomenon called electromagnetic
radiation. Electromagnetic radiation is just one of many forms of energy.
Energy is from the Greek word for “active”. Indeed, anything that moves or
changes in any way does so because of energy. Energy is defined as “the ability to
do work”.
Forms of Energy
There are many forms of energy, but they can all be put into two categories:
kinetic and potential. Kinetic energy is the energy of motion. It includes
electromagnetic radiation since this is a wave moving through the ether. Other
forms of kinetic energy include heat, sound, wind and electricity. Potential energy
is stored energy. This includes gravity, chemical and atomic energy. It is stored
until the right set of circumstances causes it to be released in a form of kinetic
energy. The food we eat contains potential energy in the cells that comprise it.
Throughout our lives we convert the stored energy in our food into the energy
required to sustain our lives and to interact with our environment.
Continuous blackbody em ission and
em ission spectra of v arious elem ents
Absorption spectra of
v arious ty pes of stars

68. 68
Energy can not be created or destroyed. It can only be converted from one form
to another. This principle is called the Conservation of energy and is considered
to be an established and accepted law of physics.
It is the consideration of light as energy that led to an understanding of the role
that atoms play in the phenomenon of light and, ultimately, to a revolution in all
of physics.
The Atomic Age
The quantum
By 1900 the world was becoming electrified. Incandescent lighting began to
replace oil and gas lanterns in factories, cities and homes. After nearly 100 years
of development, light bulbs having a reasonable life time, could be inexpensively
manufactured. Incandescent bulbs produce light by virtue of heating a thin
filament by passing electricity through it, causing the filament to glow. This is
the same kind of light that is emitted by a piece of metal (like a horseshoe) that
has been heated by a fire and is called blackbody radiation. It is also the type of
light produced by the sun and stars. Unfortunately, when it comes to producing
useful visible light, incandescent light bulbs are very inefficient and about 90% of
the electrical energy going to the bulb is converted to heat rather than light.
German physicist, Max Planck, took on research into the principles of blackbody
radiation to see how more efficient light bulbs might be produced. As matter is
heated it gives off light. At lower temperatures most of the light emitted is in the
infrared part of the spectrum. As the temperature is increased more of the
emitted light is that of visible wavelengths. The peak wavelength emitted by a
blackbody gets shorter as the temperature is increased. At about 6000 degrees C,
the blackbody produces light of all visible wavelengths and glows white. This is
the temperature that produces a distribution of visible wavelengths that match
those produced by the sun. At even higher temperatures, one would expect that
the wavelengths of light produced would continue to get shorter so that all the
emitted light would eventually migrate to the ultraviolet part of the spectrum,
but, this is not what happens. In order to derive mathematics that explained the
measurement data, Planck assumed that the atoms of the glowing matter are only
able to produce a certain minimum amount of energy at specific wavelengths at a
given temperature. In this way he quantized the energy so that it could only be
delivered in small packages rather than in a continuously varying amount. For
Planck, this was purely a mathematical trick for deriving equations that matched
the observations, and not truly the reality of the behavior of these atoms. His
calculations resulted in a constant, h, later called Planck’s constant, that, when
multiplied by the frequency of the light, v (remember frequency is the speed of
light, c, divided by its wavelength), gives the quantized amount of energy
contained in these packages. In other words, E = hv. This was the birth of
quantum physics.

69. 69
In 1905 a paper on the photoelectric effect, written by a relatively unknown
German physicist, Albert Einstein, required the use of h, Planck’s constant, in
order to correctly describe the effect mathematically. The photoelectric effect is a
phenomenon where the electrons of certain materials can be dislodged as the
consequence of absorption of energy from short wavelength electromagnetic
radiation such as visible or ultraviolet light. This was earlier described by Hertz
who noticed that the sparks generated in his spark gap receiver were much more
intense if ultraviolet light illuminated the spark gap. The absorption of this
radiation by the atoms of the metal forming the spark gap caused the electrons of
these atoms to be less tightly bound to their nuclei, allowing them to more easily
participate in electric current flow.
For reasons that could not be explained at the time, the energy imparted to each
electron was the same, regardless of the intensity of the incident light. If the
intensity was decreased, the number of electrons ejected was also decreased, but
each one ejected still carried the same energy. It was also found that for incident
light of different (longer) wavelengths no electrons were ejected, no matter how
bright the light was. This could not be explained by electro-magnetic waves.
Einstein showed that the energy of the ejected electrons depends only on the
frequency of the incident radiation and that this radiation interacted with the
electrons as if they were discrete particles with an energy given by E =hv.
Max Karl Ernst Ludwig
Planck 1858 - 1947
Blackbody radiation iselectromagnetic radiation
thatisemitted by matter when it is heated. Its
spectrum dependsonly on the temperature of the
m atter.
Photoelectric effect
Incidentradiation (the red wav es on the left)
strikesa metalsurface transferringenergy to the
electrons causingthem to eject from the surface.
The energy of the ejected electrons depends on
the frequency (hence wavelength)of the incident
radiation.

70. 70
Einstein called these light particles photons. Like the energy levels in atoms,
light, itself, was now also quantized.
Einstein - relativity
Albert Einstein went on to write over 300 scientific papers. His theories of
special and general relativity challenged the existing notions of space, time,
matter, energy and gravity and formed the bedrock of modern physics, eventually
dethroning the great Isaac Newton. They also contained some radical ideas
regarding the nature of light.
Einstein’s theory of special relativity, also published in 1905, is a theory of
constant velocity motion. The classical (Newtonian) physics of motion that
satisfied scientists for over 200 years failed to explain the results of the
Michelson-Morley experiments. In classical physics when two objects, A and B
are in motion relative to each other, A can be considered to be at rest and B to be
in motion at some speed relative to A. Conversely, B can be considered to be at
rest with A in motion. From both perspectives, or, frames of reference, any
questions regarding the time or distance traveled by either A or B will yield the
same answer from both. For example, I am driving my car at 30 miles per hour
(mph), and pass you standing at the side of the road. After I’ve gone 10 miles
past where you are standing, you throw a frisbee that travels at 40 mph in the
same direction that I am traveling. From my frame of reference, I can consider
myself to be standing still with the frisbee coming up from behind me at 10 mph.
From your frame of reference, the Frisbee is traveling 40 mph. We disagree
about the speed of the frisbee because you are standing still and I am in motion.
We are in different inertial frames of reference. We do, however, agree that it
takes 1 hour for the frisbee to catch up with me and that the frisbee traveled 40
miles, while I traveled 30 miles during that hour.
This is all in accordance with Newton’s laws of motion.
Now let’s replace the frisbee with a beam of light traveling 300 million meters per
second (c) and my car with a rocket ship travelling 100 million meters per
second. In other words, you turned on a flashlight after I passed you in my
rocket. This is the same scenario as before, except the speeds are much higher. If
I measure the speed of the light beam, relative tomy motion, I should get the

71. 71
difference of the two speeds, or 200 million meters per second, right? In fact,
what Michelson and Morley (and others) seemed to find was that the speed of
light is exactly the same no matter how they measured it, whether it was moving
with, against, or perpendicular to the motion of the Earth. Experiments show
that no matter how fast you're moving, and no matter what direction you're
moving in, relative to a light source, you get exactly the same answer when you
measure the speed of its light. Consider that the earth is traveling approximately
30,000 meters per second in its orbit around the sun. Using the interferometer,
Michelson measured the speed of light in all directions relative to the earth’s
motion and found no difference regardless of the direction of the light’s path.
The interferometer was certainly sensitive enough to see the expected difference
in light’s speed, but no difference was found. This baffled physicists and many
refused to believe it as the conviction that lightwaves require a stationary
medium in which to travel was firmly imbedded into the scientific thinking of the
time.
Einstein’s theory of special relativity was based on two principles: 1) the laws of
physics are the same in all frames of reference, and 2) the speed of light (c) is the
same for all observers regardless of their inertial frame of reference. This means
that once the beam from your flashlight has passed my rocket ship, we both see it
moving away from us at the same speed, c, even though I’m behind it moving fast
and you’re standing still. Here then, is a paradox, how can light, traveling at the
same speed for all observers, goa further distance for one observer than it does
for another in the same amount of time. Einstein said that time is the culprit,
and, because of my speed, time passes more slowly for me than it does for you.
This effect is called time dilation. If an object was able to attain the speed of
light, in the object’s frame of reference, time would stop. In other words, the
speed of light (in a vacuum) is the absolute limit to how fast an object can travel.
As objects begin to approach that unbelievably fast speed other bizarre things
happen. Besides time slowing down, the object’s mass increases and, at the speed
of light, (if it were possible for the object to go that fast), becomes infinite. This is
because of Einstein’s concept of rest energy. Rest energy is the energy that
matter contains when it is motionless. Einstein, in the most famous scientific
equation of all time, declared that E = mc². E is the amount of energy stored in
all the atoms that comprise the object, m is the object’s mass (at rest) in grams
and, of course, c is the speed of light in a vacuum. The c² makes the units of
measure come out right. In this way, matter can be thought of as “frozen” energy.
This principle is called the equivalence of matter and energy and is what led to
the atomic bomb and other, more humane uses of nuclear energy. The particles
of light, that Einstein called “photons” are the only kind of particles that have
zero rest energy and can, therefore, move that fast without becoming infinitely
massive. Any other matter, when placed into motion, acquires extra mass to
provide the extra energy necessary tosustain its motion. The effects of high
speed motion on time and mass also happen at speeds that are within our realm
of experience, but are so infinitesimally small that we do not notice them.

72. 72
Special relativity deals with the physics of constant velocity motion. The
equations do not completely describe the effects of acceleration for objects that
are speeding up, slowing down or changing direction. In order to take these
effects into account, in 1915 Einstein published his general theory of relativity. It
is mostly a theory of gravity. The Newtonian concept of gravity was that of an
attractive force connecting every object in the universe with every other object.
The larger and more massive an object is, the greater is the force of gravity it
exerts. This is how the moon is captured in orbit around the larger earth which,
in turn, is captured in orbit around the much more massive sun. In this classical
view, time and space were twodistinct concepts that formed the background in
which objects move. Einstein’s idea of gravity requires that we think of time as a
fourth dimension of three-dimensional space. In this way, space and time form
the structure of the universe called space-time. Objects having mass deform, or
curve space-time such that other objects in the vicinity will tend to fall toward
them. The conceptual model for space-time is a stretched rubber sheet. Place a
bowling ball, representing the sun for instance, in the center of the sheet. This
causes the rubber to deform under the weight of the bowling ball. If you roll a
marble, representing the earth, near the bowling ball, it will tend to roll around it.
At the right velocity and the right distance from the bowling ball, the marble will
revolve around the bowling ball indefinitely, having reached a dynamic balance
between the tendency to fall toward the bowling ball and the inertia that keeps it
at some distance away from it.
According to Einstein, since photons in motion have mass, their direction of
travel is influenced by gravity. This effect has been observed during a total solar
eclipse, when the moon is temporarily directly in line between the sun and earth.
In the shadow of the moon, stars that are behind the sun can be seen, and the
light from these stars bends toward the sun as it passes by causing the star to
appear at a slightly different location than where it really is. Gravity alsoaffects
time which slows down in deformed space-time. General relativity predicts the
Albert Einstein 1879 – 1955
GRAVITY IS THE DEFORMATION OF SPACE-
TIME BY MATTER. IT BENDS LIGHT AND
SLOWS DOWN TIME.

73. 73
existence of black holes which are considered by most scientists today to be a
confirmed phenomenon of our universe.
In laboratories around the world the effects predicted by relativity have been
observed in every experiment ever devised totest these theories. The
measurement of these effects agrees nearly perfectly with Einstein’s mathematics.
It seems that Einstein’s universe is pretty much how things really are. Relativistic
effects must be taken into account in order for GPS systems tofunction properly.
Atomic clocks, based on the frequency of radiation emitted by a specific atomic
transition for a given element, run slower when they are in motion. They also run
slower when close to the earth’s surface than they do when airborne due to the
relativistic effect of gravity on time. In particle accelerators, sub-atomic particles
like protons and electrons are accelerated to speeds approaching that of light.
These particles are found to increase in mass exactly as Einstein’s theory predicts.
Einstein’s theories also predicted the possibility of lasers fifty years before their
invention.
Einstein’s theory of special relativity deals with the very fast. His theory of
general relativity deals with the very large. Much of today’s activity in physics
deals with the very small. It is called quantum physics and has been at the
forefront of all the major breakthroughs over the past century. The language of
quantum physics is the language of high level mathematical probability and
statistics. It is a language unto itself, whose implications often defy common
sense or explanation. Although many of the concepts of quantum physics have
been around for more than 100 years, scientists have only scratched the surface
of its implications. Nevertheless, its principles are being exploited in
laboratories, factories, hospitals and homes around the world.
Quantum mechanics
Just before 1900, it became clear that classical physics was unable to explain
certain phenomena. Coming to terms with these limitations led to the
development of quantum mechanics, a major revolution in physics. Quantum
mechanics is the body of scientific principles which attempts to explain the
behavior of matter and its interactions with energy on the scale of atoms and
atomic particles.

74. 74
Light comes from atoms
In 1913 Niels Bohr proposed a model of the atom that included quantized
electron orbits. In Bohr's model, electrons could inhabit only certain orbits
around the atomic nucleus.
When an atom absorbs energy, an electron jumps (transitions) from an orbit of
lower energy to one of higher energy.
When an electron transitions from an orbit of higher energy to one of lower
energy, the atom can emit a photon of light.
Transitions from higher to lower energy states (decay) are the natural tendency
as the atom can typically only store energy in this fashion for a short time. The
energy of the emitted photon is determined by the difference in energy between
the atomic transition orbits (also called energy levels). In accordance with
Plank’s law (E=hv). Like Maxwell’s dipole antenna, where oscillating electric
charges radiate radio frequency light, the atoms and molecules that compose
matter also produce oscillating electric charges producing higher frequency
This simple atom
consists of a nucleus
(containing the protons
and neutrons) and an
electron cloud. The
electrons circle the
nucleus in discrete
orbits. Each of these
orbits corresponds to
different energy levels
of the atom.
Absorption of energy:
An atom absorbs energy in
the form of heat, light, or
electricity. Electrons may
move from a lower-energy
orbit toa higher-energy
orbit. The electron is said
tobe in an exited state.
Emission of a photon:
Excited electrons naturally
transition from a higher toa
lower energy orbit releasing
energy in the form of a light
photon. The emitted photon
emitted has a very specific
wavelength (color).

75. 75
(shorter wavelength) light. The absorption and emission lines of hydrogen, for
instance, are at the wavelengths that they are because of the permitted energy
levels that are specific to hydrogen’s atomic structure. Each of these lines
corresponds to an allowed energy level transition involving an increase or
reduction of the atom’s energy. Emission and absorption lines for each element
are like a fingerprint and extend over the entire electromagnetic spectrum, not
just in the visible portion.
Wave-particle duality
As we have seen, light exhibits properties of both waves and particles.
In 1924, Louis de Broglie proposed the idea that just as light has both wave-like
and particle-like properties, matter also has wave-like properties. The
wavelength associated with a particle is related to its momentum such that λ =
h/p where λ is the wavelength of the so-called matter wave, p is the momentum
and h is Planck’s constant.
This relationship, called the de Broglie hypothesis, holds for all types of matter.
Thus all matter exhibits properties of both particles and waves. This is the
concept of wave-particle duality. Neither the classical concepts of "particle" or
"wave" can fully describe the behavior of quantum-scale objects, either photons
or matter. Wave-particle duality is the principle behind electron microscopy.
Visible wavelength absorption
and emission lines of hy drogen
Louis DeBroglie (1892 – 1987)

76. 76
An electron microscope is a type of microscope that uses a particle beam of
electrons to illuminate the specimen and produce a magnified image. Electron
microscopes have a greater resolving power than optical microscopes, because
electrons have wavelengths about 100,000 times shorter than visible light and
can achieve magnifications of up to about 10,000,000x, whereas ordinary light
microscopes are limited by diffraction to magnifications below 2000x.
The wave-like nature of electrons as well as other sub-atomic particles of matter
has been demonstrated in laboratories. These particles, when passed through a
double slit, like that used by Thomas Young to demonstrate the wave nature of
light, exhibit diffraction and interference just as light waves do. Similar wave-
like phenomena were later shown for atoms and even small molecules.
Schroedinger’s equation
In 1925, building on de Broglie's hypothesis, Erwin Schrödinger developed the
equation that describes the behavior of a quantum mechanical wave. The
equation, called the Schrödinger equation after its creator, is central to quantum
mechanics, and defines the permitted stationary states of a quantum system, and
describes how the quantum state of a physical system changes in time.
Schrödinger was able to calculate the energy levels of hydrogen by treating a
hydrogen atom's electron as a classical wave, moving in a well of electrical
potential created by the proton. This calculation accurately reproduced the
energy levels of the Bohr model.
Particles of matter(electrons)can
exhibit wave properties.
Matterwaves
S = λL/d where:
S is the fringe spacing
λ is the wavelength
L is the distance from slits toscreen
d is the spacing between the slits

77. 77
Uncertainty principle
It is not possible to know the values of all of the properties of the system at the
same time. Those properties that are not known with precision must be
described by probabilities. Suppose that we want to measure the position and
speed of an object, for example, a car going through a radar speed trap. We
assume that the car has a definite position and speed at a particular moment in
time, and how accurately we can measure these values depends on the quality of
our measuring equipment. If we improve the precision of our measuring
equipment, we will get a result that is closer to the true value. In particular, we
would assume that how precisely we measure the speed of the car does not affect
its position, and vice versa.
In 1927, Heisenberg proved that these assumptions are not correct. Quantum
mechanics shows that certain pairs of physical properties, like position and
speed, cannot both be known to arbitrary precision: the more precisely one
property is known, the less precisely the other can be known. This statement is
known as the uncertainty principle. The uncertainty principle isn't a statement
about the accuracy of our measuring equipment, but about the nature of the
system itself. Our assumption that the car had a definite position and speed was
incorrect. On a scale of cars and people, these uncertainties are too small to
notice, but when dealing with atoms and electrons they become critical.
The uncertainty principle shows mathematically that the product of the
uncertainty in the position and momentum of a particle (momentum is velocity
multiplied by mass) could never be less than a certain value, and that this value is
related to Planck's constant.
Erwin Schrödinger (1887 – 1961)

78. 78
The Copenhagen interpretation
Bohr, Heisenberg and others tried to explain what these experimental results and
mathematical models really mean. Their description, known as the Copenhagen
interpretation of quantum mechanics, attempts to describe the nature of reality
that was being probed by the measurements and described by the mathematical
formulations of quantum mechanics.
The main principles of the Copenhagen interpretation are:
1. A system is completely described by a wave function, ψ. (Heisenberg)
2. How ψ changes over time is given by the Schrödinger equation.
3. The description of nature is essentially probabilistic. The probability of an
event — for example, where on the screen a particle will show up in the
two slit experiment — is related to the square of the amplitude of its wave
function. (Born rule, due to Max Born, which gives a physical meaning to
the wavefunction in the Copenhagen interpretation: the probability
amplitude)
4. It is not possible to know the values of all of the properties of the system at
the same time; those properties that are not known with precision must be
described by probabilities. (Heisenberg's uncertainty principle)
5. Matter, like energy, exhibits a wave-particle duality. An experiment can
demonstrate the particle-like properties of matter, or its wave-like
properties; but not both at the same time. Measuring devices are
essentially classical devices, and measure classical properties such as
position and momentum.
6. The quantum mechanical description of large systems should closely
approximate the classical description.
Werner Heisenberg (1901 – 1976)
Heisenberguncertainty principle

79. 79
Quantum phenomena
Fluorescence
Fluorescence is the emission of light by a substance that has absorbed light or
other electromagnetic radiation of a different wavelength. It is a form of
luminescence. In most cases, the emitted light has a longer wavelength, and
therefore lower energy, than the absorbed radiation. However, when the
absorbed electromagnetic radiation is intense, it is possible for one electron to
absorb two photons; this two-photon absorption can lead to emission of radiation
having a shorter wavelength than the absorbed radiation.
The most striking examples of fluorescence occur when the absorbed radiation is
in the ultraviolet region of the spectrum and the emitted light is in the visible
region.
Fluorescence has many practical applications, including mineralogy, gemology,
chemical sensors, fluorescence spectroscopy, fluorescent labeling, dyes, biological
detectors and fluorescent lamps.
Fluorescence lifetime refers tothe average time the molecule stays in its excited
state before emitting a photon usually between 1 and 20 nanoseconds.
The fluorescence quantum yield (Ф) gives the efficiency of the fluorescence
process. It is defined as the ratio of the number of photons emitted to the number
of photons absorbed.
Fluorescentmineralsemitvisible lightwhen exposed to
ultrav iolet light

80. 80
Photosynthesis
Photosynthesis is a chemical process that converts carbon dioxide into organic
compounds, especially sugars, using the energy from sunlight. Photosynthesis
occurs in plants, algae, and many species of bacteria. Photosynthetic organisms
are called photoautotrophs, since they can create their own food. In plants, algae,
and bacteria, photosynthesis uses carbon dioxide and water, releasing oxygen as
a waste product. Photosynthesis is vital for all life on Earth. As well as
maintaining the normal level of oxygen in the atmosphere, nearly all life either
depends on it, either as a direct source of energy, or indirectly, as the ultimate
source of the energy in their food (the exceptions are chemoautotrophs that live
in rocks or around deep sea hydrothermal vents). The rate of energy capture by
photosynthesis is immense, approximately 100 terawatts, which is about six
times larger than the power consumption of human civilization. As well as
energy, photosynthesis is also the source of the carbon in all the organic
compounds within organisms' bodies. In all, photosynthetic organisms convert
around 100–115 petagrams of carbon into biomass per year. In the light
reactions, one molecule of the pigment chlorophyll absorbs one photon and loses
one electron. The chlorophyll molecule regains the lost electron from a water
molecule through a process called photolysis, which releases a dioxygen (O2 )
molecule. The overall equation for the light-dependent reactions under the
conditions of non-cyclic electron flow in green plants is:
2 H2 O + 2 NADP+ + 3 ADP + 3 Pi + light → 2 NADPH + 2 H+ + 3 ATP + O2
Not all wavelengths of light can support photosynthesis. The photosynthetic
action spectrum depends on the type of accessory pigments present. For example,
in green plants, the action spectrum resembles the absorption spectrum for
chlorophylls and carotenoids with peaks for violet-blue and red light. In red
algae, the action spectrum overlaps with the absorption spectrum of phycobilins
for red blue-green light, which allows these algae to grow in deeper waters that
filter out the longer wavelengths used by green plants. The non-absorbed part of
the light spectrum is what gives photosynthetic organisms their color (e.g., green
plants, red algae, purple bacteria) and is the least effective for photosynthesis in
the respective organisms.
The leaf is the prim ary site of
photosy nthesis in plants.

81. 81
Quantum tunneling
Quantum tunneling refers to the quantum mechanical phenomenon where a
particle tunnels through a barrier that it classically could not surmount. The
effect was predicted in the early 20th century, and its acceptance as a general,
physical phenomenon came mid-century.
As a consequence of the wave-particle duality of matter, tunneling is often
explained using the Heisenberg uncertainty principle. Purely quantum
mechanical concepts are central to the phenomenon, so quantum tunneling is
one of the defining features of quantum mechanics and the particle-wave duality
of matter. Quantum tunneling is in the domain of quantum mechanics, the study
of what happens at the quantum scale. This process cannot be directly perceived,
so much of its understanding is shaped by the macroscopic world, which classical
mechanics can adequately explain. Particles in that realm are understood to
travel between potential barriers as a ball rolls over a hill; if the ball does not have
enough energy to surmount the hill, it comes back down. The twoforms of
mechanics differ in their treatment of this scenario. Classical mechanics predicts
that particles that do not have enough energy to classically surmount a barrier
will not be able to reach the other side. In quantum mechanics, these particles
can, with a very small probability, tunnel to the other side, thus crossing the
barrier. The reason for this difference comes from the treatment of matter in
quantum mechanics as having properties of waves and particles. One
interpretation of this duality involves the Heisenberg uncertainty principle,
which defines a limit on how precisely the position and the momentum of a
particle can be known at the same time. For a quantum particle moving against a
potential hill, the wave function describing the particle can extend tothe other
side of the hill. It is as if the particle has 'dug' through the hill.

82. 82
Particles that have tunneled through such a barrier do at superluminal (faster
than light) speed. In research carried out in the United States, particle physicists
have shown that light pulses can be accelerated to up to 300 times their normal
velocity of 186,000 miles per second.
Separate experiments show that in certain circumstances photons - the particles
of which light is made - could apparently jump between two points separated by a
barrier in what appears to be zero time.
The implications are mind-boggling. According to one interpretation it means
that light will arrive at its destination before it has started its journey, in effect,
leaping forward in time.
The research is already causing controversy among physicists. What bothers
them is that if light could travel forward in time it could carry information. This
would breach one of the basic principles in physics - causality, which says that a
cause must come before an effect. It would also shatter Einstein’s theory of
relativity since it depends in part on the speed of light being unbreakable.
Dr Guenter Nimtz, of Cologne University, an expert in the field, agrees. He
believes that information can be sent faster than light, but that this will not
breach the principle of causality because the time taken to interpret the signal
would fritter away all the savings.
"The most likely application for this is not in time travel but in speeding up the
way signals move through computer circuits," he said.
In the new world that modern science is beginning to perceive, sub-atomic
particles can apparently exist in two places at the same time - making no
distinction between space and time.
Diagram of the Nim tz and
Stahlhofen double prism
experim ent. A beam of
m icrowaves (33mm wavelength) is
directed toward a pair of prism s.
The prism angles prov ided for
totalinternalreflection setting up
an evanescentwave. Because the
second prism is close to the first
prism,some light tunnelled across
the air gap (frustrated total
internal reflection). The
transmitted and reflected wav es
arrived at detectors at the sam e
time,despite the transmitted light
havingalso traversed the distan ce
of the gap.This isthe basisfor the
assertion of faster -than-c
transm ission of inform ation.
Photonscanbe detected behind
the right-hand prism until the gap
exceeds about one m eter.
Günter Nim tz
(1936 - PRESENT)

83. 83
Stopping light
Entanglement
Twoentangled particles, which can include photons moving at the speed of light,
have properties that are linked. Measuring the properties of one of these items
will cause the other to instantly switch from an indeterminate state to one with
properties defined by its entanglement with the other. Since the entangled items
can be far apart when this occurs, the transfer of properties appears to be taking
place faster than the speed of light.
Albert Einstein coined the phrase “spooky action at a distance” to describe this
phenomenon in which particles appear to instantaneously influence each other
even when they are kilometers apart. Today, scientists call it quantum
entanglement, and it forms a cornerstone of the quantum world. One way to
create entangled photons is to shine a laser at a particular type of crystal. The
crystal will split some of the photons in two, resulting in two photons whose
combined energy and momentum match that of the original photon. The twoare
now linked even if they travel far apart. Depending on their techniques, scientists
In 2001 Lene Vestergard Hau and her
team at Harvard stopped light for 1.5
seconds in a Bose-Enistein condensate, a
new form of matter made by cooling
sodium atoms to billionths of a degree
above absolute zero. The normally opaque
condensate temporarily traps a pulse of
laser light by converting it to matter waves.
Another specially tuned laser turns the
condensate transparent releasing the light
pulse. Possible applications include
ultrafast optical computing and
communications.Lene Vestergaard Hau 1959 - Present

84. 84
can entangle photons in numerous ways and make the particles’ properties match
or differ. One property that can exhibit the phenomenon is polarization, the
direction of oscillations of the light waves. Until measured, both linked photons
are in a superposition of states — horizontally and vertically polarized at the same
time.
If the detector records a vertical polarization state for one photon, then (for one
entangling technique) it will be instantly known that the partner photon is
horizontally polarized. The very act of measuring one seems to determine what
the other will be, even though the twoare so far apart that information couldn’t
travel between them unless it traveled faster than light.
The findings may make it look as if one measurement caused the other to come
out a certain way, but that is not the case. Suppose the second photon was
measured in a different reference frame, say speeding along on a rocket ship, it
could look as if the second measurement came first. Scientists still can’t fully
explain this quantum link.
Lasers
In 1917, Albert Einstein established the theoretical foundations for the laser in his
paper “On the Quantum Theory of Radiation”. Theodore H. Maiman invented
and operated the first functioning laser at Hughes Research Laboratory on May
16, 1960. Maiman’s laser employed a solid-state flashlamp-pumped synthetic
ruby crystal toproduce red laser light, at 694 nanometers wavelength. When
lasers were invented in 1960, they were called "a solution looking for a problem".
Since then, they have become commonplace, finding utility in thousands of
highly varied applications in every sector of modern society, including consumer
electronics, information technology, science, medicine, industry, law
enforcement, entertainment, and the military.
The first use of lasers in the daily lives of the general population was the
supermarket barcode scanner, introduced in 1974. The laserdisc player,
introduced in 1978, was the first successful consumer product to include a laser
but the compact disc player was the first laser-equipped device to become
common, beginning in 1982 followed shortly by laser printers.
Some other uses are:
 Medicine: Bloodless surgery, laser healing, surgical treatment, kidney
stone treatment, eye treatment, dentistry
 Industry: Cutting, welding, material heat treatment, marking parts, non-
contact measurement of parts
 Military: Marking targets, guiding munitions, missile defense, electro-
optical countermeasures (EOCM), alternative to radar, blinding troops.
 Law enforcement: used for latent fingerprint detection in the forensic
identification field

85. 85
 Research: Spectroscopy, laser ablation, laser annealing, laser scattering,
laser interferometry, LIDAR, laser capture microdissection, fluorescence
microscopy
 Product development/commercial: laser printers, optical discs (e.g. CDs
and the like), barcode scanners, thermometers, laser pointers, holograms,
 Laser lighting displays: Laser light shows
 Cosmetic skin treatments: acne treatment, cellulite and striae reduction,
and hair removal.
How do lasers work?
As discussed earlier, atoms can store energy through absorption. When energy is
absorbed the electrons of atoms are raised to a state of higher energy. After a
very short time these electrons naturally relax to a lower energy state and, in the
process, release the stored energy. The released energy may be in the form of
heat or it may be absorbed by other nearby atoms. It can also be emitted in the
form of a photon of light. This is called spontaneous emission. Almost all light
sources produce light resulting from this process.
The light from lasers is produced by a process called stimulated emission. In this
case, the electron has been induced to relax to a state of lower energy sooner than
it ordinarily would. This results in light that has some very special properties.
A laser is a device that controls the way that energized atoms release photons.
The word “laser” is an acronym that means Light Amplification by Stimulated
Emission of Radiation, which describes how a laser works.
Although there are many types of lasers, all have certain essential features. In a
laser, the lasing medium is “pumped” to get the atoms into an excited state.
Typically, very intense flashes of light or electrical discharges pump the lasing
medium and create a large collection of excited-state atoms (atoms with higher-
Absorption of energy: An atom absorbs energy
in the form of heat, light, or electricity .
Electrons may move from a lower-energy orbit
to a higher-energy orbit. The electron is said to
be in an exited state.
Em ission of a photon:
Excited electronsnaturally transition from a
higher to a lower energy orbit releasing
energy in the form of a light photon. The
em itted photon emitted has a v ery specific
wav elength (color).

86. 86
energy electrons). It is necessary tohave a large collection of atoms in the excited
state for the laser to work efficiently. In general, the atoms are excited to a level
that is two or three levels above the ground state. This increases the degree of
population inversion. The population inversion is the number of atoms in the
excited state versus the number in ground state. When population inversion has
been achieved the lasing medium becomes a light amplifier.
Once the lasing medium is pumped, it contains an arrangement of atoms with
most of its electrons sitting in excited levels. The excited electrons have energies
greater than the more relaxed electrons. Just as the electron absorbed some
amount of energy toreach this excited level, it can also release this energy. As the
figure below illustrates, the electron can simply relax, and in turn rid itself of
some energy. This emitted energy comes in the form of photons (light energy).
The photon emitted has a very specific wavelength (color) that depends on the
state of the electron's energy when the photon is released. Twoidentical atoms
with electrons in identical states will release photons with identical wavelengths.
Laser light is very different from normal light. Laser light has the following
properties:
 The light released is monochromatic. It contains one specific
wavelength of light (one specific color). The wavelength of light is
determined by the amount of energy released when the electron drops to a
lower orbit.
 The light released is coherent. It is “organized” -- each photon moves in
step with the others. This means that all of the photons have wave fronts
that launch in unison.
 The light is very directional. A laser light has a very tight beam and is
very strong and concentrated. A flashlight, on the other hand, releases
light in many directions, and the light is very weak and diffuse.
Tomake these three properties occur takes something called stimulated
emission. This does not occur in your ordinary flashlight -- in a flashlight, all of

87. 87
the atoms release their photons randomly. In stimulated emission, photon
emission is organized.
The photon that any atom releases has a certain wavelength that is dependent on
the energy difference between the excited state and the ground state. If this
photon (possessing a certain energy and phase) should encounter another atom
that has an electron in the same excited state, stimulated emission can occur. The
first photon can stimulate or induce atomic emission such that the subsequent
emitted photon (from the second atom) vibrates with the same frequency and
direction as the incoming photon.
Idealized 3-level system

88. 88
The other key to a laser is a pair of mirrors, one at each end of the lasing medium.
Photons, with a very specific wavelength and phase, reflect off the mirrors to
travel back and forth through the lasing medium. In the process, they stimulate
other electrons to make the downward energy jump and can cause the emission
of more photons of the same wavelength and phase. A cascade effect occurs, and
soon we have propagated many, many photons of the same wavelength and
phase. The mirror at one end of the laser is "half-silvered," meaning it reflects
some light and lets some light through. The light that makes it through is the
laser light.
You can see all of these components in the following figures which illustrate how
a simple ruby laser works.
A ruby laser consists of a flash tube (typically a very bright gas arc lamp), a ruby
rod and two mirrors (one half-silvered). The ruby rod is the lasing medium and
the flash tube pumps it.
1. The laser in its non-lasing state. The atoms of the ruby rod are in the
state of lowest energy, called the ground state.

89. 89
2. The flash tube fires and bombards the ruby rod with visible light. The light
excites atoms in the ruby. This is called “pumping” because energy from the flash
tube is pumped into the atoms of the ruby crystal raising their electrons to higher
energy levels. Eventually more atoms are in states of higher energy than in the
ground state. This condition is called population inversion.
3. Some of these atoms spontaneously emit photons in all directions as their
electrons spontaneously relax to a lower energy state.

90. 90
4. Some of the photons move in a direction parallel to the ruby's axis, bouncing
back and forth between the mirrors. As they pass through the crystal, they
stimulate emission in other atoms. With each pass the light becomes more intense
(amplified) because of the increasing number of photons being emitted.
5. Monochromatic (nearly single wavelength), coherent (all waves are in phase),
highly directional laser light leaves the ruby through the half-silvered mirror.
There are many different types of lasers. The laser medium can be a solid, gas,
liquid or semiconductor. Lasers are commonly designated by the type of lasing
material employed:

91. 91
 Solid-state lasers have lasing material distributed in a solid matrix
(such as the ruby or neodymium:yttrium-aluminum garnet "Yag" lasers).
The neodymium-Yag laser emits infrared light at 1064 nanometers (nm).
A ruby laser is a solid-state laser and emits at a wavelength of 694 nm.
 Gas lasers helium-neon (HeNe) is the most common of the gas lasers
having a primary output of visible red light at 632.8nm. CO2 lasers emit
energy in the far-infrared (10,600nm), and are used for cutting hard
materials.
 Excimer lasers (the name is derived from the terms excited and dimers)
use reactive gases, such as chlorine and fluorine, mixed with inert gases
such as argon, krypton or xenon. When electrically stimulated, a pseudo
molecule (dimer) is produced. When lased, the dimer produces light in the
ultraviolet range. These have applications as surgical lasers and in
semiconductor fabrication.
 Dye lasers use complex organic dyes, such as rhodamine 6G, in liquid
solution or suspension as lasing media. They are tunable over a broad
range of wavelengths and capable of producing ultrashort pulses.
 Semiconductor lasers, sometimes called diode lasers, are not solid-
state lasers. These electronic devices are generally very small and use low
power such as those used in laser pointers. They may be built into larger
arrays, such as the writing source in some laser printers or CD players.
Diode laser arrays are also used as a pump source for certain solid state
lasers. These are typically much more energy efficient than flashlamps
sources
 Here are some typical lasers and their emission wavelengths:
Laser Type Wavelength (nm)
Argon fluoride (UV) Gas (excimer) 193
Xenon chloride (UV) Gas (excimer) 308
Nitrogen (UV) Gas 337
Argon (blue) Gas 488
Argon (green) Gas 514
Helium neon (red) Gas 633
Rhodamine 6G dye (tunable) Dye 570-650
Titanium Sapphire (tunable) Solid state 650-1100
Aluminum Gallium Indium
Phosphide (red)
Semiconductor
670
Ruby (CrAlO3) (red) Solid state 694
Aluminum Gallium Arsenide (NIR) Semiconductor 785, 808
Nd:Yag (NIR) Solid state 1064
Carbon dioxide (FIR) Gas 10600

92. 92
Modes of operation
A laser can be classified as operating in either continuous or pulsed mode,
depending on whether the power output is essentially continuous over time or
whether its output takes the form of pulses of light on one or another time scale.
Of course even a laser whose output is normally continuous can be intentionally
turned on and off at some rate in order to create pulses of light. When the
modulation rate is on time scales much slower than the cavity lifetime and the
time period over which energy can be stored in the lasing medium or pumping
mechanism, then it is still classified as a "modulated" or "pulsed" continuous
wave laser. Most laser diodes used in communication systems fall in that
category.
Continuous wave operation
Some applications of lasers depend on a beam whose output power is constant
over time. Such a laser is known as continuous wave (CW). Many types of lasers
can be made to operate in continuous wave mode to satisfy such an application.
Many of these lasers actually lase in several longitudinal modes at the same time,
and beats between the slightly different optical frequencies of those oscillations
will in fact produce amplitude variations on time scales shorter than the round-
trip time (the reciprocal of the frequency spacing between modes), typically a few
nanoseconds or less. In most cases these lasers are still termed "continuous
wave" as their output power is steady when averaged over any longer time
periods, with the very high frequency power variations having little or no impact
in the intended application. (However the term is not applied to mode locked
lasers, where the intention is to create very short pulses at the rate of the round-
trip time).
For continuous wave operation it is required for the population inversion of the
gain medium to be continually replenished by a steady pump source. In some
lasing media this is impossible. In some other lasers it would require pumping
the laser at a very high continuous power level which would be impractical or
destroy the laser by producing excessive heat. Such lasers cannot be run in CW
mode.
Pulsed operation
Pulsed operation of lasers refers toany laser not classified as continuous wave, so
that the optical power appears in pulses of some duration at some repetition rate.
This encompasses a wide range of technologies addressing a number of different
motivations. Some lasers are pulsed simply because they cannot be run in
continuous mode.
In other cases the application requires the production of pulses having as large an
energy as possible. Since the pulse energy is equal to the average power divided
by the repetition rate, this goal can sometimes be satisfied by lowering the rate of

93. 93
pulses so that more energy can be built up in between pulses. In laser ablation for
example, a small volume of material at the surface of a work piece can be
evaporated if it is heated in a very short time, whereas supplying the energy
gradually would allow for the heat to be absorbed into the bulk of the piece, never
attaining a sufficiently high temperature at a particular point.
Other applications rely on the peak pulse power (rather than the energy in the
pulse), especially in order to obtain nonlinear optical effects. For a given pulse
energy, this requires creating pulses of the shortest possible duration utilizing
techniques such as Q-switching.
Q-switching
In a Q-switched laser, the population inversion is allowed to build up by
introducing loss inside the resonator which exceeds the gain of the medium; this
can also be described as a reduction of the quality factor or 'Q' of the cavity. Then,
after the pump energy stored in the laser medium has approached the maximum
possible level, the introduced loss mechanism (often an electro- or acousto-
optical element) is rapidly removed (or that occurs by itself in a passive device),
allowing lasing to begin which rapidly obtains the stored energy in the gain
medium. This results in a short pulse incorporating that energy, and thus a high
peak power.
Mode-locking
A mode-locked laser is capable of emitting extremely short pulses on the order of
tens of picoseconds down to less than 10 femtoseconds. These pulses will repeat
at the round trip time, that is, the time that it takes light to complete one round
trip between the mirrors comprising the resonator. Due to the Fourier limit (also
known as energy-time uncertainty), a pulse of such short temporal length has a
spectrum spread over a considerable bandwidth. Thus such a gain medium must
have a gain bandwidth sufficiently broad to amplify those frequencies. An
example of a suitable material is titanium-doped, artificially grown sapphire
(Ti:sapphire) which has a very wide gain bandwidth and can thus produce pulses
of only a few femtoseconds (10-15) duration.
Such mode-locked lasers are a most versatile tool for researching processes
occurring on extremely short time scales (known as femtosecond physics,
femtosecond chemistry and ultrafast science), for maximizing the effect of
nonlinearity in optical materials (e.g. in second-harmonic generation, parametric
down-conversion, optical parametric oscillators and the like) due to the large
peak power, and in ablation applications. Again, because of the extremely short
pulse duration, such a laser will produce pulses which achieve an extremely high
peak power.

94. 94
Pulsed pumping
Another method of achieving pulsed laser operation is to pump the laser material
with a source that is itself pulsed, either through electronic charging in the case of
flash lamps, or another laser which is already pulsed. Pulsed pumping was
historically used with dye lasers where the inverted population lifetime of a dye
molecule was so short that a high energy, fast pump was needed. The way to
overcome this problem was to charge up large capacitors which are then switched
to discharge through flashlamps, producing an intense flash. Pulsed pumping is
also required for three-level lasers in which the lower energy level rapidly
becomes highly populated preventing further lasing until those atoms relax to the
ground state. These lasers, such as the excimer laser and the copper vapor laser,
can never be operated in CW mode.
Harmonic generation
Using certain non-linear optical crystals it is possible to convert laser light of a
given frequency into laser light having a frequency that is an integer multiple of
the initial frequency. This process, also called sum frequency generation,
typically requires pulsed laser light of relatively high power and small bandwidth.
Second harmonic generation (SHG; also called frequency doubling) is an optical
process in which photons interacting with the nonlinear material are effectively
"combined" to form new photons with twice the frequency, twice the energy and
half the wavelength of the initial photons. For instance, the 1064nm wavelength
output of a Nd:YAG laser can be directed to a properly coated potassium titanyl
phosphate (KTP) crystal toconvert approximately 50% of the near-infrared laser
light to green laser light having half the wavelength, that is 532nm.
It is also possible to generate higher harmonics as in third and fourth harmonic
generation (frequency tripling and quadrupling respectively). Crystals such as
lithium niobate (LiNbO3), titanyl phosphate (KTP), potassium niobate (KNbO3)
and beta barium borate (BBO) can be used in harmonic generation.

95. 95
Where does light come from?
Any light that you see is made up of a collection of one or more photons
propagating through space as electromagnetic waves. In total darkness, our eyes
are actually able to sense single photons, but generally what we see in our daily
lives comes to us in the form of trillions of photons produced by light sources and
reflected off objects. If you look around you right now, there is probably a light
source in the room producing photons, and objects in the room that reflect those
photons. Your eyes absorb some of the photons reflected from objects in the
room, and that is how you see.
There are many different ways toproduce photons, but all of them use the same
mechanism inside an atom to do it. This mechanism involves the energizing of
electrons orbiting each atom's nucleus. For example, hydrogen atoms have one
electron orbiting the nucleus. Helium atoms have two electrons orbiting the
nucleus. Aluminum atoms have 13 electrons orbiting the nucleus. Each atom has
a preferred number of electrons orbiting its nucleus.
Electrons circle the nucleus in fixed orbits -- a simplified way to think about it is
to imagine how satellites orbit the Earth. There's a huge amount of theory around
electron orbitals, but to understand light there is just one key fact to understand:
An electron has a natural orbit that it occupies, but if you energize an atom you
can move its electrons to higher orbitals. A photon of light is produced whenever
an electron in a higher-than-normal orbit falls back to its normal orbit. During
the fall from high-energy to normal-energy, the electron emits a photon -- a
packet of energy -- with very specific characteristics. The photon has a frequency,
or color, that exactly matches the distance the electron falls.
Probably the most common way toenergize atoms is with heat, and this is the
basis of incandescence. If you heat up a horseshoe with a blowtorch, it will
eventually get red hot, and if you heat it enough it gets white hot. Red is the
lowest-energy visible light, so in a red-hot object the atoms are just getting
enough energy to begin emitting light that we can see. Once you apply enough
heat to cause white light, you are energizing so many different electrons in so
many different ways that all of the colors are being generated -- they all mix
together to look white. A normal 75-watt incandescent bulb is generating light
by using electricity to create heat. However, there are lots of other ways to
generate light, some of which are listed below:
 Halogen lamps - Halogen lamps use electricity to generate heat, but
benefit from a technique that lets the filament run hotter.
 Gas lanterns - A gas lantern uses a fuel like natural gas or kerosene as
the source of heat.
 Fluorescent lights - Fluorescent lights use electricity to directly
energize atoms rather than requiring heat.
 Lasers - Lasers use energy to"pump" a lasing medium, and all of the
energized atoms are made to dump their energy at the exact same
wavelength and phase.

96. 96
 Glow-in-the-dark toys - In a glow-in-the-dark toy, the electrons are
energized but fall back to lower-energy orbitals over a long period of
time, so the toy can glow for awhile.
 Chemical light sticks - A chemical light stick and, for that matter,
fireflies, use a chemical reaction to energize atoms.
 The sun (and stars) – Within the sun’s core hydrogen atoms are
under such great gravitational force that the matter within their nuclei
is “pulled together” undergoing nuclear fusion which converts the
hydrogen atoms into helium atoms. In this way, millions of tons of
this matter is converted to energy every second. This energy leaves the
Sun as radiation, and the part of this radiation that constitutes visible
light is what makes the Sun shine.
The thing to note from this list is that anything that produces light does it by
energizing atoms in some way.
The following is a list of Wikepedia links to information on various light
sources:
Natural
 Astronomical objects
o Stars
o Star clusters
o Galaxies
o Nebulae
o quasars
o accretion disks
 Bioluminescence
o Fireflies
o Glowworms
o Aequorea victoria (a type of jellyfish)
o Antarctic krill
o Lux operon
 Lightning
 Aurorae
 Sunlight (Solar radiation)
o Skylight
o Moonlight (via reflection)
o planets (via reflection)
o comets (via reflection)
o asteroids (via reflection)
 Triboluminescence

97. 97
Direct chemical
 Chemoluminescence (Lightsticks)
 Fluorescence
 Phosphorescence
Combustion-based
See also: Combustion
 Argon flash
 Acetylene/Carbide lamps
 Betty lamp
 Butter lamp
 Candles
 Fire
 Gas lighting
 Kerosene lamps
 Lanterns
 Limelights
 Oil lamps
 Rushlights
 Safety lamps
o Davy lamps
o Geordie lamps
 Torches
Electric
Arc lamps
Main article: Arc lamp
 Yablochkov candles
Incandescent lamps
See also: Incandescence
 Carbon button lamp
 Conventional incandescent light bulbs
o Flashlight
 Globar
 Nernst lamp
Electroluminescent (EL) lamps
Main article: Electroluminescence

98. 98
LED / semiconductor
 Light-emitting diodes
o Organic light-emitting diodes
o Polymer light-emitting diodes
o Solid-state lighting
o LED lamp
Gas discharge lamps
 Fluorescent lamps
o Compact fluorescent lamps
o Black light
 Inductive lighting
 Hollow cathode lamp
 Neon and argon lamps
 Plasma lamps
 Xenon flash lamps
High-intensity discharge lamps
 Ceramic discharge metal halide lamps
 Hydrargyrum medium-arc iodide (HMI) lamps
 Mercury-vapor lamps
 Metal halide lamps
 Sodium vapor lamps
 Xenon arc lamps
 Sulfur lamps
Nuclear
 Radioluminescent paint (formerly used on watch and clock dials)
 Self-powered lighting
Other
 Blackbody radiation
 Bremsstrahlung
 Cherenkov radiation
 Cyclotron radiation
 Fusor
 Lasers, Laser diode
 Sonoluminescence
 Sulfur lamp
 Synchrotron light, see also Synchrotron radiation

99. 99
How light interacts with matter
The effects that light has on matter and that matter has on light depend upon the
properties of the incident light and the properties of the matter it encounters.
One or more of the properties of light: direction, velocity, intensity, spectrum or
polarization is usually changed when light is incident on matter. Properties of
the matter also change as a result of incident light. This change may be
permanent or temporary depending on the atomic structure of the matter.
When a light wave hits an object, what happens to it depends on the energy of the
light wave, the natural frequency at which electrons vibrate in the material and
the strength with which the atoms in the material hold on to their electrons.
Based on these three factors, four different things can happen when light hits an
object:
 The waves can be reflected or scattered off the object.
 The waves can be absorbed by the object.
 The waves can be refracted through the object.
 The waves can pass through the object with no effect. (transmission)
And more than one of these possibilities can happen at once.
Transmission
If the frequency or energy of the incoming light wave is much higher or much
lower than the frequency needed to make the electrons in the material vibrate,
then the electrons will not capture the energy of the light, and the wave will
pass through the material unchanged. As a result, the material will be
transparent to that frequency of light.
Most materials are transparent to some frequencies, but not to others. For
example, high frequency light, such as gamma rays and X-rays, will pass through
ordinary glass, but lower frequency ultraviolet and infrared light will not.
The amount of light transmitted by a material is equal to the total amount
incident on the material minus losses. These losses can occur as a result of
reflection, absorption and scattering or any combination thereof.

100. 100
Reflection
Reflection changes the direction and intensity of incident light. The atoms in
some materials hold on to their electrons loosely. In other words, the materials
contain many free electrons that can jump readily from one atom to another
within the material. When the electrons in this type of material absorb energy
from an incoming light wave, they do not pass that energy on to other atoms. The
energized electrons merely vibrate and then send the energy back out of the
object as a light wave with the same frequency as the incoming wave. The overall
effect is that the light wave does not penetrate deeply into the material.
In most metals, electrons are held loosely, and are free to move around, so these
metals reflect visible light and appear to be shiny. The electrons in glass have
some freedom, though not as much as in metals. Toa lesser degree, glass reflects
light and appears to be shiny, as well.
A reflected wave always comes off the surface of a material at an angle equal to
the angle at which the incoming wave hit the surface. In physics, this is called the
Law of Reflectance. You have probably heard the Law of Reflectance stated as
"the angle of incidence equals the angle of reflection."
Dispersion
Dispersion ofa light beam in a prism.

101. 101
Dispersion is a bi-product of refraction that causes the separation of a wave into
spectral components which have different wavelengths, due to a dependence of
the wave's speed on its wavelength. The most commonly seen consequence of
dispersion in optics is the separation of white light into a color spectrum by a
prism. From Snell's law it can be seen that the angle of refraction depends on the
refractive index of the prism material. Since the refractive index varies with
wavelength, it follows that the angle that the light is refracted towill also vary
with wavelength, causing an angular separation of the colors. For visible light,
most transparent materials (e.g. glasses) have:
that is, the refractive index n decreases with increasing wavelength λ.
At the interface of such a material with air or vacuum (index of ~1), Snell's law
predicts that light incident at an angle θ to the normal will be refracted at an
angle
Arcsin( sin (θ) / n). Thus, blue light, with a higher refractive index, will be bent
more strongly than red light, resulting in the well-known rainbow pattern.
Absorption
Absorption changes the intensity and the transmitted spectrum of incident light.
In absorption, the frequency of the incoming light wave is at or near the vibration
frequency of certain electrons in the material. The electrons take in the energy of
the light wave and start tovibrate. What happens next depends upon how tightly
the atoms hold on to their electrons. Absorption occurs when the electrons are
held tightly, and they pass the vibrations along to the nuclei of the atoms. This
makes the atoms speed up, collide with other atoms in the material, and then give
up the energy they acquired from the vibrations as heat.
The absorption of light makes an object dark or opaque to the frequency of the
incoming wave. Wood is opaque to visible light. Some materials are opaque to
some frequencies of light, but transparent to others. Glass is opaque to
ultraviolet light, but transparent to visible light. For most substances, the
amount of absorption varies with the wavelength of the light, leading to the
appearance of color in pigments that absorb some wavelengths but not others.
For example, an object that absorbs blue, green and yellow light will appear red
when viewed under white light. More precise measurements at many

102. 102
wavelengths allow the identification of a substance via absorption spectroscopy.
Absorption spectroscopy is based on the absorption of photons by one or more
substances present in a sample, which can be a solid, liquid, or gas, and
subsequent transition of electrons from a lower to a higher energy level. Note
that the sample can be a pure, homogeneous substance or a complex mixture.
The wavelength at which the incident photon is absorbed is determined by the
difference in the available energy levels of the various types of atoms present in
the sample. It is the wavelength selectivity of these atoms that gives absorbance
spectroscopy much of its utility. Typically, X-rays are used to reveal chemical
composition, and near ultraviolet to near infrared wavelengths are used to
distinguish the configurations of various isomers in detail. In absorption
spectroscopy the absorbed photons are not re-emitted (as in fluorescence) rather,
the energy that is transferred tothe chemical compound upon absorbance of a
photon is lost by non-radiative means, such as transfer of energy as heat to other
molecules. UV-visible spectroscopy refers to techniques where one measures
how much light of a particular wavelength is absorbed by a sample. Since
wavelength can often be correlated with the presence and or structure of a
particular chemical, absorbance spectroscopy is widely used for both qualitative
(is a chemical present?) and quantitative (how much?) work in a wide range of
fields. For instance, DNA absorbs light in the UV range so the amount of DNA in
a sample can be determined by measuring the absorbance of UV light.
Scattering
Scattering changes the direction, intensity and polarization state of incident light.
Scattering is merely reflection off a rough surface. Incoming light waves get
reflected at all sorts of angles, because the surface is uneven. The surface of
paper is a good example. You can see just how rough it is if you look at it under a
microscope. When light hits paper, the waves are reflected in all directions. This
is what makes paper so incredibly useful -- you can read the words on a printed
page regardless of the angle at which your eyes view the surface.
Another interesting rough surface is Earth's atmosphere. You probably don't
think of the atmosphere as a surface, but it nonetheless is "rough" to incoming
white light. The atmosphere contains molecules of many different sizes, including
nitrogen, oxygen, water vapor and various pollutants. This assortment scatters
the higher energy light waves, the ones we see as blue light. This is why the sky
looks blue. Light scattering is one of the two major physical processes that
contribute to the visible appearance of most objects, the other being selective

103. 103
absorption. Surfaces described as white owe their appearance almost completely
to the scattering of light by the surface of the object. The absence of surface
scattering leads to a shiny or glossy appearance. The types of non-uniformities
that can cause scattering, sometimes known as scatterers or scattering centers,
are too numerous to list, but a small sample includes particles, bubbles, droplets,
density fluctuations in fluids, defects in crystalline solids, surface roughness, cells
in organisms, and textile fibers in clothing. The effects of such features on the
path of almost any type of propagating wave or moving particle can be described
in the framework of scattering theory.

104. 104
GLASS
The discovery ofglass
Natural glass has existed since the beginnings of time, formed when certain types
of rocks melt as a result of high-temperature phenomena such as volcanic
eruptions, lightning strikes or the impact of meteorites, and then cool and solidify
rapidly. Stone-age man is believed to have used cutting tools made of obsidian (a
natural glass of volcanic origin.
According to the ancient-Roman historian Pliny (AD 23-79), Phoenician
merchants transporting stone actually discovered glass (or rather became aware
of its existence accidentally) in the region of Syria around 5000 BC. Pliny tells
how the merchants, after landing, rested cooking pots on blocks of nitrate placed
by their fire. With the intense heat of the fire, the blocks eventually melted and
mixed with the sand of the beach to form an opaque liquid.
Man-made glass
The earliest man-made glass objects, mainly non-transparent glass beads, are
thought to date back to around 3500 BC, with artifacts being found in Egypt and
Eastern Mesopotamia (corresponding to modern-day Iraq, northeastern Syria,
southeastern Turkey and southwestern Iran). In the third millennium, in central
Mesopotamia, the basic raw materials of glass were being used principally to
produce glazes on pots and vases. The discovery may have been coincidental,
with calciferous sand finding its way into an overheated kiln and combining with
soda to form a colored glaze on the ceramics. Phoenician merchants and sailors
began to spread this new art along the coasts of the Mediterranean.
The oldest fragments of glass vases (evidence of the origins of the hollow glass
industry), however, date back to the 16th century BC and were found in
Mesopotamia. Hollow glass production was also evolving around this time in
Egypt, and there is evidence of other ancient glassmaking activities emerging
independently in Greece, Austria and China.
Early hollowglass production
After 1500 BC, Egyptian craftsmen are known to have begun developing a
method for producing glass pots by dipping a core mold of compacted sand into
molten glass and then turning the mold so that molten glass adhered to it. While
still soft, the glass-covered mold could then be rolled on a slab of stone in order to
smooth or decorate it. The earliest examples of Egyptian glassware are three
vases bearing the name of the Pharaoh Thoutmosis III (1504-1450 BC), who
brought glassmakers to Egypt as prisoners following a successful military

105. 105
campaign in Asia.
There is little evidence of further development until the 9th century BC, when
glassmaking was revived in Mesopotamia from where it is thought to have spread
to Italy.
The first glassmaking "manual" dates back to around 650 BC. Instructions on
how to make glass are contained in tablets from the library of the Assyrian king
Ashurbanipal (669-626 BC).
A major breakthrough in glassmaking was the discovery of glassblowing some
time between 27 BC and AD 14, attributed to Syrian craftsmen from the Sidon-
Babylon area. The long thin metal tube used in the blowing process has changed
very little since then. In the last century BC, the ancient Romans then began
blowing glass inside molds, greatly increasing the variety of shapes possible for
hollow glass items.
The Roman connection
The Romans also did much to spread glassmaking technology. With its
conquests, trade relations, road building, and effective political and economical
administration, the Roman Empire created the conditions for the flourishing of
glassworks across western Europe and the Mediterranean. During the reign of
the emperor Augustus, glass objects began to appear throughout Italy, in France,
Germany and Switzerland. Roman glass has even been found as far as China,
shipped there along the silk routes.
It was the Romans who began to use glass for architectural purposes, with the
discovery of clear glass (through the introduction of manganese oxide) in
Alexandria around AD 100. Cast glass windows, albeit with poor optical
qualities, began to appear in the most important buildings in Rome.
With the geographical division of the empires, glass craftsmen began to migrate
less, and eastern and western glassware gradually acquired more distinct
characteristics. Alexandria remained the most important glassmaking area in the

106. 106
East, producing luxury glass items mainly for export. In Rome's Western empire,
the city of Köln in the Germany developed as the hub of the glassmaking
industry, adopting mainly eastern techniques. Then, with the decline of the
Roman Empire and culture, progress in the field of glassmaking slowed
dramatically over the next five hundred years.
The early Middle Ages
By the year 1000, significant changes in European glassmaking techniques had
taken place. Because of the difficulties in importing raw materials, soda glass
was gradually replaced by glass made using the potash obtained from the burning
of trees. At this point, glass made north of the Alps began to differ from glass
made in the Mediterranean area where soda ash was still the dominant raw
material.
Sheet glass
The 11th century alsosaw the development by German glass craftsmen of a
technique - then further developed by Venetian craftsmen in the 13th century -
for the production of glass sheets. By blowing a hollow glass sphere and swinging
it vertically, gravity would pull the glass into a hollow cylindrical “pod” measuring
as much as 3 meters long and a half meter wide. While still hot, the ends of the
pod were cut off and the resulting cylinder cut lengthways and laid flat. Other
types of sheet glass included crown glass (also known as "bullions"), relatively
common across western Europe. With this technique, a glass ball was blown and,
while in a semi-molten state, quickly spun to flatten and increase in size, up to a
limited diameter. The panes thus created would then be joined with lead strips
and pieced together to create windows. Glazing remained, however, a great
luxury up to the late Middle Ages, with royal palaces and churches the most likely
buildings to have glass windows. Stained glass windows reached their peak as
the Middle Ages drew to a close, with an increasing number of public buildings,
inns and the homes of the wealthy fitted with clear or colored glass decorated
with historical scenes and coats of arms.

107. 107
In the Middle Ages, the Italian city of Venice assumed its role as the glassmaking
center of the western world. The Venetian merchant fleet ruled the
Mediterranean waves and helped supply Venice's glass craftsmen with the
technical know-how of their counterparts in Syria, and with the artistic influence
of Islam.
The importance of the glass industry in Venice can be in the number of craftsmen
at work there (more than 8,000 at one point). A 1271 ordinance laid down
certain legal measures such as a ban on imports of foreign glass and a ban on
foreign glassmakers who wished to work in Venice in order to protect the
manufacturing trade secrets developed there.
Until the end of the 13th century, most glassmaking in Venice took place in the
city itself, however, the frequent fires caused by the furnaces led the city
authorities, in 1291, toorder the transfer of glassmaking to the island of Murano.
The measure also made it easier for the city to keep an eye on what was one of its
main assets, ensuring that no glassmaking skills or secrets were exported.
Another Italian glassmaking industry developed at Altare, near Genoa. Its
importance lies largely in the fact that it was not subject to the strict statutes of
Venice with regard to the exporting of glass working skills. During the 16th
century, craftsmen from Altare helped extend the new styles and techniques of
Italian glass to other parts of Europe, particularly France.
Lead crystal
The development of lead crystal has been attributed to the English glassmaker
George Ravenscroft (1618-1681), whopatented his new glass in 1674. He had
been commissioned to find a substitute for the Venetian crystal produced in
Murano and based on pure quartz sand and potash. By using higher proportions
of lead oxide instead of potash, he succeeded in producing a brilliant glass with a
high refractive index which was very well suited for deep cutting and engraving.
Advances from France

108. 108
In 1688, in France, a new process was developed for the production of plate glass,
principally for use in mirrors, whose optical qualities had, until then, left much to
be desired. The molten glass was poured onto a special table and rolled out flat.
After cooling, the plate glass was ground on large round tables by means of
rotating cast iron discs and increasingly fine abrasive sands, and then polished
using felt disks. The result of this "plate pouring" process was flat glass with good
optical transmission qualities. When coated on one side with a reflective, low
melting metal, high-quality mirrors could be produced.
France also took steps to promote its own glass industry and attract glass experts
from Venice. This was not an easy move for the Venetian workers given the
history of discouragement of such behavior (At one point, Venetian glass
craftsmen faced death threats if they disclosed glassmaking secrets or took their
skills abroad). The French court, for its part, placed heavy duties on glass
imports and offered Venetian glassmakers a number of incentives such as French
nationality after eight years and total exemption from taxes.
From craft to industry
It was not until the latter stages of the Industrial Revolution, however, that
mechanical technology for mass production and in-depth scientific research into
the relationship between the composition of glass and its physical qualities began
to appear in the industry.
A key figure and one of the forefathers of modern glass research was the German
scientist OttoSchott (1851-1935), whoused scientific methods to study the effects
of numerous chemical elements on the optical and thermal properties of glass. In
the field of optical glass, Schott teamed up with Ernst Abbe (1840-1905), a
professor at the University of Jena and joint owner of the Carl Zeiss firm, to make
significant technological advances
Another major contributor in the evolution towards mass production was
Friedrich Siemens, who invented the tank furnace. This rapidly replaced the old
pot furnace and allowed the continuous production of far greater quantities of
molten glass.
Increasing automation
Towards the end of the 19th century, the American engineer Michael Owens
(1859-1923) invented an automatic bottle blowing machine which arrived in
Europe after the turn of the century. Owens was backed financially by E.D.L.
Libbey, owner of the Libbey Glass Co. of Toledo, Ohio. By the year 1920, in the
United States, there were around 200 automatic Owens Libbey Suction Blow
machines operating. In Europe, smaller, more versatile machines from
companies like O'Neill, Miller and Lynch were also popular.
Added impetus was given to automatic production processes in 1923 with the

109. 109
development of the gob feeder, which ensured the rapid supply of more
consistently sized gobs in bottle production. Soon afterwards, in 1925, IS
(individual section) machines were developed. Used in conjunction with the gob
feeders, IS machines allowed the simultaneous production of a number of bottles
from one piece of equipment. The gob feeder-IS machine combination remains
the basis of most automatic glass container production today.
Modern flat glass technology
In the production of flat glass (where, as explained earlier, molten glass had
previously been poured onto large tables then rolled flat into "plates", cooled,
ground and polished before being turned over and given the same treatment on
the other surface), the first real innovation came in 1905 when a Belgian named
Fourcault managed to vertically draw a continuous sheet of glass of a consistent
width from the tank. Commercial production of sheet glass using the Fourcault
process eventually got under way in 1914.
Around the end of the First World War, another Belgian engineer Emil Bicheroux
developed a process whereby the molten glass was poured from a pot directly
through tworollers. Like the Fourcault method, this resulted in glass with a more
even thickness, and made grinding and polishing easier and more economical.
Another float process developed after the Second World War by Britain's
Pilkington Brothers Ltd., and introduced in 1959, combined the brilliant finish of
sheet glass with the optical qualities of plate glass. Molten glass, when poured
across the surface of a bath of molten tin, spreads and flattens before being
drawn horizontally in a continuous ribbon into the annealing oven.
Optical glass
Optical glass is a specialty product which is designed for use in optical devices
such as telescopes, binoculars, eyeglasses, and so forth. This glass is formulated
very precisely toensure that it is free of impurities and produced under the right
conditions so that its properties are known. High quality optical glasses can be
quite expensive, as they require a great deal of work to produce. People have
been exploring optical glass since the 17th century when glass workers began
refining existing techniques to create glass which could be used to create lenses.
These early lenses were used in simple microscopes and corrective vision devices.
While the quality of this optical glass was not very good when compared to
modern glass, it did establish the fact that glass had a range of potential uses, and
that refinement of glass making techniques could result in even better lenses and
optics.
A number of things go into the construction of optical glass. The components of
the glass must be carefully controlled, to ensure that it has the right balance of
minerals, and it must be manufactured in environments where the temperatures

110. 110
can be very precisely regulated. Optical glass may also require special tempering
during the manufacturing process, with the goal being a clear glass with a high
refractive index. The precise parameters for the glass vary, depending on how it
is to be used.
Once the glass is made, it can be cut and ground into lenses and prisms for
various applications. Depending on how a lens is cut and ground, it will behave
in different ways, allowing it to be used to correct vision, take photographs, or
scan the heavens to look at the stars.
What makes glass transparent?
Glass is so common that most of us take it completely for granted. But just what
is it about glass that makes it transparent? Why can we see through a window and
not through the wooden frame that surrounds it?
You have probably noticed that most liquids and gases are transparent. Water,
cooking oil, rubbing alcohol, air, natural gas, etc. are all clear. That's because of a
fundamental difference between solids, liquids and gases. When a substance is in
its solid state, normally its molecules are highly organized in relation to one
another, strengthening the bond between them and giving the substance rigidity.
As the substance changes from a solid to a liquid, however, the strength of the
bond lessens and the molecules begin to align themselves randomly. If we follow
the substance's progression to a gas, we see that the molecular bond is greatly
weakened and the relationship of the molecules to one another is almost
completely random.
This progression from ordered to random organization is the primary reason that
light can pass through liquids and gases. Just like bricks stacked neatly on top of
one another, the ordered molecules of most solids are virtually impenetrable to
light waves. Depending on the substance, the light waves will be reflected,
scattered, absorbed or, more likely, some combination of the three. But as the
substance changes to liquid or gas and the molecules are not stacked neatly
anymore, gaps and holes occur that allow portions of the light waves topass
through. The greater the randomness of the molecular organization of the
substance, the easier it is for the light to pass through.
Another factor happens at the sub-atomic level. The atoms that bind together to
make the molecules of any particular substance have electrons, usually lots of
them. When photons come in contact with these electrons, the following can
occur:

111. 111
 An electron absorbs the energy of the photon and transforms it (usually
into heat)
 An electron absorbs the energy of the photon and stores it (this can
result in luminescence, which is called fluorescence if the electron
stores the energy for a short time and phosphorescence if it stores it
for long time)
 An electron absorbs the energy of the photon and sends it back out the
way it came in (reflection)
 An electron cannot absorb the energy of the photon, in which case the
photon continues on its path (transmitted)
Most of the time, it is a combination of the above that happens to the light that
hits an object. The electrons in different materials vary in the range of energy that
they can absorb. A lot of glass, for example, blocks out ultraviolet (UV) light.
What happens is the electrons in the glass absorb the energy of the photons in the
UV range while ignoring the weaker energy of photons in the visible light
spectrum. If the electrons absorb the energy of any portion of the visible
spectrum, the light that transmits through will appeared colored according to the
portion of the spectrum absorbed. In fact, the color of any object is a direct result
of what levels of energy the electrons in the substance will absorb!
Although forms of glass, such as obsidian or volcanic glass, can occur naturally,
Glass is generally a manmade substance. Here is the basic way to make glass:
 Take the most common glass material, silica, which is just plain old
sand like you would find on the beach.
 Heat it to an extreme temperature until it becomes liquid, then cool it.
The resulting substance has a molecular structure that is very random like a
liquid yet that retains the strong bond and rigidity of a solid. This is a
simplification of the process. Usually you add both a substance to make the silica
melt quicker and something else to stabilize it so that the glass is not brittle and
easily broken. The temperature, heating time and cooling method must all be
very exact.
The materials used for glass-making cool to form an amorphous mix of molecules
(like a liquid) and have electrons that do not absorb the energy of photons in the
visible spectrum. This is why you can see through glass, but not wood, metal or
stone, which are all solids.
A similar method, called quenching, is used with plastics to make them
transparent or translucent. Quenching causes the polymers (long-chain
molecules) in the plastic to settle into a random pattern that allows light to pass
through. You can even use this process with organic substances. Clear or
translucent candy is created by heating the ingredients of the recipe and then
rapidly cooling them.
Notice that clear glass, clear plastic and clear candy are all solids that are melted
and then cooled. Same process!
Thousands of different substances are used to make various forms of glass. How

112. 112
much and what type of light is transmitted depends on the type and purity of the
substance used. Silica, in its purest form, transmits light well. Very little of the
light wave is absorbed, but some of it is usually reflected. Look at almost any
window and you will see this is true.
Other materials used to make glass may transmit or block specific types of light,
such as ultraviolet light, or even parts of the visible spectrum. You have probably
seen glass that was black or some other opaque color. Most often the color is
caused by microscopic particles suspended in the glass, like the impurities we
talked about in some liquids and gases. Another way to change the properties of
the glass, such as filtering specific wavelengths of light, is to slow down the
cooling process enough to allow the molecules to partially crystallize, or form
patterns. And finally, some materials are chosen because they can be shaped and
made to transmit and/or refract light in specific ways touse, for instance, as
eyeglass lenses or as a magnifying glass. There are thousands of formulations
used to manufacture optical grade glass affording designers options that can
tailored to the specific application. These options include differences in optical,
chemical, thermal and mechanical properties.
OPTICAL PROPERTIES
Refractive index is a measure of the speed of light in the glass compared with
that in a vacuum. It determines how much light bends when traveling, from an
adjacent medium, into and out of the glass. The higher the index, the more
bending occurs. The amount of light reflected from a glass surface also depends
on the index; a material with higher index reflects more light than one with lower
index.
Homogeneity is the maximum variation of the refractive index within a volume
of glass.
Striae is localized, usually thread-like inclusions in glass that vary in index from
the surrounding material. The different striae grades limit the amount and
direction of striae present in a volume of glass.
Stress birefringence in glass is residual strain that results from limitations in
the annealing process. This can cause changes to the polarization state of light
propagating through the glass causing a relative phase shift between orthogonal
polarization orientations. Stress birefringence that is possible within a volume of
glass is given in units of nm/cm (nanometers of phase shift between S and P
polarized light after propagating through 1 cm of glass.
Dispersion is a measure of how the refractive index of a glass material varies
with wavelength. Since the index of glass is higher for short wavelengths, such as
blue light, than it is for longer wavelengths, like red light, blue light bends more
than red light. This is why a glass prism separates the component colors
comprising white light. The dispersion of glass materials can be stated at any
wavelength(s), but manufacturers provide the Abbe value (vd) for these materials
which is given by: vd = (nd – 1) / (nF-nC) where:

113. 113
nd = the index at 587.6nm
nF = the index at 486.1nm and
nC = the index at 656.3nm
Glasses having a nd > 1.60 and a vd > 50 or nd < 1.60 and a vd > 55 are
commonly called “crowns”. Others are called “flints”. By designing a lens
comprised of a negative flint lens used in conjunction with a positive crown lens
the effects of chromatic aberrations can be minimized. This type of lens is called
an achromat.
Transmittance is a measure of the percentage of light that passes through a
polished plane-parallel optical window at normal incidence (perpendicular to the
polished surfaces). This is a function of the chemical constituents of the optical
material and varies with wavelength. Most clear optical glass transmits well
(>90%) across the visible range (400nm to 700nm) but can vary considerably
with regard to UV and IR transmittance. The light that does not get transmitted
is lost due to reflection from both surfaces and material absorption. The loss due
to surface reflection is a constant for any given wavelength, but the loss due to
absorption depends on the thickness of the material through which the light
passes. For this reason, in order to calculate absorption losses at a specific
wavelength and a specific thickness, it is necessary toremove the loss due to
reflection and consider only the internal transmittance. This is
accomplished through the reflection factor (P).
P = 2n / (n2 +1) where n is the index for the material at a specific wavelength.
The relationship between transmittance (T) and internal transmittance (Ti) is
given by:
Ti = T / P
Glass data sheets typically provide the internal transmittance for a given glass
type at many wavelengths and for a given thickness (D1 ). From this one can
calculate the internal transmittance for a given wavelength at any thickness using
the following relationship:
log Ti / log Ti2 = d1 / d2 where:

114. 114
Ti is the known internal transmittance at thickness d1
d2 is the thickness for which the internal transmittance is being calculated
Ti2 is the calculated internal transmittance at thickness d2
For many applications it is desirable to transmit certain wavelengths and not
others. Filter glass formulations are available for accomplishing that. There are
four basic types of filter glass materials:
Short pass filters transmit short wavelengths and absorb longer wavelengths.
Long pass filters transmit long wavelengths and absorb shorter wavelengths.
Bandpass filters transmit a range of wavelengths and absorb wavelengths that
are both shorter and longer than those included in the transmission range.
Neutral density filters are designed to attenuate a specific percentage of light
regardless of the wavelength.
CHEMICAL PROPERTIES
Climate resistance (CR) is a measure of how a polished surface can change
due to high humidity and elevated temperature exposure. In sensitive materials
the surface change is visible in the form of a cloudy film that can not be removed
except by repolishing. Samples are exposed to a water-vapor saturated (100%
relative humidity) atmosphere and alternated in temperature between 45°C and
55°C in one hour cycles. Each cycle causes condensation to form on the surface
and then dry. Samples are assessed after having been exposed for 30, 100 and
180 hours by measuring the amount of light scattered from the surface. Glass
types are graded into one of four classes for climatic resistance.
Resistance to staining (FR) is a measure of the discoloration of a polished
surface when exposed to a small amount of slightly acidic solution. Twosolutions
are used. Solution 1 has a pH of 4.6 and solution 2 has a pH of 5.6. The
particular stain class is determined by the time it takes for the surface to develop
a visible bluish brown stain.
Resistance to acids (SR) is a measure of possible discoloration, dissolution or
decomposition that can occur when optical glass is exposed to large quantities of
an aggressive acid solution (pH 0.3). The acid resistance class is determined by
the time it takes for the surface to develop a visible bluish brown stain. For glass
types having acid resistance lower than SR4 (color change in less than 6 minutes),
a weaker acid solution is used (pH 4.6). These sensitive glass types are classified
differently than more resistive types.

115. 115
Resistance to alkalis (AR) is a measure of possible surface decomposition
resulting from exposure to strong alkalis. The alkali resistance class is
determined by the time it takes for the surface to develop one of the following
symptoms after exposure to an alkali solution with pH 10:
a visible bluish brown stain
scarred surface but no color change
interference colors
whitish stain
white coating in thick layers
THERMAL PROPERTIES
Thermal expansion
Virtually all materials expand when they are heated. Any increase in temperature
is accompanied by an increase in volume due to thermal expansion. The graph
below depicts this general change in volume for glass materials.
Section A of the graph shows a fairly constant increase in volume over a
temperature range of 0 degrees to 300 degrees Kelvin. (-273°C to 27°C). From
300 degrees Kelvin to some point above 600 degrees Kelvin (27°C to 327°) the

116. 116
change in volume continues to increase uniformly, but at a higher rate as Section
B of the graph depicts. With further increase in temperature there is a range
(Section C) where the thermal expansion rises sharply. This is called the
transformation range. At temperatures beyond the transformation range the
increase in volume is once again linear but increases at a much higher rate. The
temperature at which the slopes of the curve on either side of the transformation
range intersect is called the transformation temperature (Tg). Since the thermal
expansion of glass depends on the temperature, manufacturers provide two
values for thermal expansion. a-30/+70°C is the thermal expansion within the
temperature range of -30°C to 70°C and a+20/+300°C is the thermal expansion
within the temperature range of 20°C to 300°C. These are typically expressed in
parts per million per degree Kelvin (10-6/K).
Viscosity
Viscosity refers to how easily a material will flow. Molasses has a higher viscosity
than water. Solids have a higher viscosity than liquids. As glass materials are
heated they transform from a solid, brittle state through a state where they
become softer and less brittle and then to a pourable, liquid state and finally to a
point of vaporization or gaseous state. The chart below depicts this behavior.
At low temperatures glass is in the solid state and has a high viscosity.

117. 117
At the transformation temperature (Tg) the viscosity of most optical glass is
approximately 1013dPa s. By heating glass to a temperature of 5°C to 15°C above
the transformation temperature, and then slowly and uniformly cooling it down.
internal mechanical stresses within the material can be completely relieved. This
is called annealing and improves the index homogeneity and the mechanical
stability of the material.
At some temperature above the transformation temperature the glass has a
viscosity low enough to begin deforming under its own weight (slumping). This
is called the softening temperature (T107.6) and is defined as the temperature that
results in a viscosity of 107.6dPa s.
At some higher temperature the viscosity decreases to 104 dPa s. At this viscosity
glass can be pressed or poured into molds.
Glass manufacturers typically provide temperature values for Tg, a-30/+70°C,
a+20/+300°C, and T107.6.
MECHANICAL PROPERTIES
Density
The density of glass, like the density of any material, is the mass, in grams,
divided by the volume, in cubic centimeters.
Hardness
Different glass types can vary significantly in their hardness. Most
manufacturers specify the hardness of optical glasses using the Knoop hardness
index. This is derived by measuring the penetration of the surface by a standard
diamond that is pressed for a given amount of time under a given bearing force.
Other technical specifications for glass types can be found on the data sheets
provided by optical glass manufacturers. The following is the Schott glass data
sheet for N-BK7, a very common optical glass:

118. 118

119. 119
Astronomy with invisible light
Gamma-rays
Gamma-rays have the smallest wavelengths and the most energy of any other
wave in the electromagnetic spectrum. These waves are generated by radioactive
atoms and in nuclear explosions. Gamma-rays can kill living cells, a fact which
medicine uses to its advantage, using gamma-rays to kill cancerous cells.
Gamma-rays travel to us across vast distances of the universe, only to be
absorbed by the Earth's atmosphere. Different wavelengths of light penetrate the
Earth's atmosphere to different depths. Instruments aboard high-altitude
balloons and satellites like the Compton Observatory provide our only view of the
gamma-ray sky.
Gamma-rays are the most energetic form of light and are produced by the hottest
regions of the universe. They are also produced by such violent events as
supernova explosions or the destruction of atoms, and by less dramatic events,
such as the decay of radioactive material in space. Things like supernova
explosions (the way massive stars die), neutron stars and pulsars, and black holes
are all sources of celestial gamma-rays.

120. 120
Perhaps the most spectacular discovery in gamma-ray astronomy came in the late
1960s and early 1970s. Detectors on board the Vela satellite series, originally
military satellites, began to record bursts of gamma-rays -- not from Earth, but
from deep space!
Gamma-ray bursts can release more energy in 10 seconds than the Sun will emit
in its entire 10 billion-year lifetime! So far, it appears that all of the bursts we
have observed have come from outside the Milky Way Galaxy. Scientists believe
that a gamma-ray burst will occur once every few million years here in the Milky
Way, and in fact may occur once every several hundred million years within a few
thousand light-years of Earth.
Studied for over 25 years now with instruments on board a variety of satellites
and space probes, including Soviet Venera spacecraft and the Pioneer Venus
Orbiter, the sources of these enigmatic high-energy flashes remain a mystery.
By solving the mystery of gamma-ray bursts, scientists hope to gain further
knowledge of the origins of the Universe, the rate at which the Universe is
expanding, and the size of the Universe.

121. 121
X-rays
As the wavelengths of light decrease, they increase in energy. X-rays have smaller
wavelengths and therefore higher energy than ultraviolet waves. We usually talk
about X-rays in terms of their energy rather than wavelength. This is partially
because X-rays have very small wavelengths. It is also because X-ray light tends
to act more like a particle than a wave. X-ray detectors collect actual photons of
X-ray light - which is very different from the radio telescopes that have large
dishes designed to focus radio waves!
The Earth's atmosphere is thick enough that virtually no X-rays are able to
penetrate from outer space all the way tothe Earth's surface. This is good for us
but also bad for astronomy - we have to put X-ray telescopes and detectors on
satellites! We cannot do X-ray astronomy from the ground.
We use satellites with X-ray detectors on them to do X-ray astronomy. In
astronomy, things that emit X-rays (for example, black holes) are like the
dentist's X-ray machine, and the detector on the satellite is like the X-ray film. X-
ray detectors collect individual X-rays (photons of X-ray light) and things like the
number of photons collected, the energy of the photons collected, or how fast the
photons are detected, can tell us things about the object that is emitting them.
Tothe right is an image of
a real X-ray detector. This
instrument is called the
Proportional Counter
Array and it is on the Rossi
X-ray Timing Explorer
(RXTE) satellite. It looks
very different from
anything you might see at
a dentist's office!

122. 122
What does X-ray light show us?
Many things in space emit X-rays, among them are black holes, neutron stars,
binary star systems, supernova remnants, stars, the Sun, and even some comets!
The Earth glows in many kinds of light, including the energetic X-ray band.
Actually, the Earth itself does not glow - only aurora produced high in the Earth's
atmosphere. These aurora are caused by charged particles from the Sun.
Tothe left is the first picture of the
Earth in X-rays, taken in March,
1996 with the orbiting Polar satellite.
The area of brightest X-ray emission
is red. The energetic charged
particles from the Sun that cause
aurora also energize electrons in the
Earth's magnetosphere. These
electrons move along the Earth's
magnetic field and eventually strike
the Earth's ionosphere, causing the
X-ray emission. These X-rays are not
dangerous because they are
absorbed by lower parts of the
Earth's atmosphere. (The above
caption and image are from the
Astronomy Picture of the Day for
December 30, 1996.)

123. 123
Ultraviolet Waves
Scientists have divided the ultraviolet part of the spectrum into three regions: the
near ultraviolet, the far ultraviolet, and the extreme ultraviolet. The three regions
are distinguished by how energetic the ultraviolet radiation is, and by the
"wavelength" of the ultraviolet light, which is related to energy.
The near ultraviolet, abbreviated NUV, is the light closest to optical or visible
light. The extreme ultraviolet, abbreviated EUV, is the ultraviolet light closest to
X-rays, and is the most energetic of the three types. The far ultraviolet,
abbreviated FUV, lies between the near and extreme ultraviolet regions. It is the
least explored of the three regions.
Our Sun emits light at all the
different wavelengths in
electromagnetic spectrum, but it is
ultraviolet waves that are responsible
for causing our sunburns. Tothe left
is an image of the Sun taken at an
Extreme Ultraviolet wavelength - 171
Angstroms to be exact. (An
Angstrom is a unit length equal to
10-10 meters.) This image was taken
by a satellite named SOHO and it
shows what the Sun looked like on
April 24, 2000.
Though some ultraviolet waves from the Sun penetrate Earth's atmosphere, most
of them are blocked from entering by various gases like ozone. Some days, more
ultraviolet waves get through our atmosphere. Scientists have developed a UV
index to help people protect themselves from these harmful ultraviolet waves.

124. 124
How do we "see" using Ultraviolet light?
It is good for humans that we are protected from getting too much ultraviolet
radiation, but it is bad for scientists! Astronomers have to put ultraviolet
telescopes on satellites to measure the ultraviolet light from stars and galaxies -
and even closer things like the Sun!
There are many different satellites
that help us study ultraviolet
astronomy. Many of them only
detect a small portion of UV light.
For example, the Hubble Space
Telescope observes stars and
galaxies mostly in near ultraviolet
light. NASA's Extreme Ultraviolet
Explorer satellite is currently
exploring the extreme ultraviolet
universe. The International
Ultraviolet Explorer (IUE)
satellite has observed in the far
and near ultraviolet regions for
over 17 years.

125. 125
The Infrared
Infrared
How can we "see" using the Infrared?
Since the primary source of infrared radiation is heat or thermal radiation, any
object which has a temperature radiates in the infrared. Even objects that we
think of as being very cold, such as an ice cube, emit infrared. When an object
is not quite hot enough to radiate visible light, it will emit most of its energy in
the infrared. For example, hot charcoal may not give off light but it does emit
infrared radiation which we feel as heat. The warmer the object, the more
infrared radiation it emits.
Humans, at normal body temperature, radiate most
strongly in the infrared at a wavelength of about 10
microns. The image to the right shows a man holding
up a lighted match. Which parts of this image do you
think have the warmest temperature? How does the
temperature of this man's glasses compare to the
temperature of his hand?

126. 126
Tomake infrared pictures like the one
above, we can use special cameras and
film that detect differences in
temperature, and then assign different
brightnesses or false colors to them. This
provides a picture that our eyes can
interpret.
The image at the left shows a cat in the
infrared. The orange areas are the
warmest and the white-blue areas are
the coldest. This image gives us a
different view of a familiar animal as
well as information that we could not get
from a visible light picture.
Humans may not be able to see infrared light, but did you know that snakes in
the pit viper family, like rattlesnakes, have sensory "pits", which are used to
image infrared light? This allows the snake to detect warm blooded animals,
even in dark burrows! Snakes with 2 sensory pits are even thought to have
some depth perception in the infrared.
Many things besides people and animals emit infrared light - the Earth, the
Sun, and far away things like stars and galaxies do also! For a view from Earth
orbit, whether we are looking out into space or down at Earth, we can use
instruments on board satellites.
This is an infrared image of the Earth taken by
the GOES 6 satellite in 1986. A scientist used
temperatures todetermine which parts of the
image were from clouds and which were land
and sea. Based on these temperature
differences, he colored each separately using
256 colors, giving the image a realistic
appearance.
Why use the infrared to image the Earth?
While it is easier to distinguish clouds from
land in the visible range, there is more detail
in the clouds in the infrared. This is great for
studying cloud structure. For instance, note
that darker clouds are warmer, while lighter
clouds are cooler.

127. 127
Microwaves
What do Microwaves show us?
Because microwaves can penetrate haze,
light rain and snow, clouds and smoke,
these waves are good for viewing the Earth
from space.
The ERS-1 satellite sends out wavelengths
about 5.7 cm long (C-band). This image
shows sea ice breaking off the shores of
Alaska.
The JERS satellite uses wavelengths
about 20 cm in length (L-band). This is an
image of the Amazon River in Brazil.
This is a radar image acquired from the
Space Shuttle. It also used a wavelength
in the L-band of the microwave spectrum.
Here we see a computer enhanced radar
image of some mountains on the edge of
Salt Lake City, Utah.

128. 128
In the 1960's a startling discovery was made quite by accident. A pair of scientists
at Bell Laboratories detected background noise using a special low noise antenna.
The strange thing about the noise was that it was coming from every direction
and did not seem to vary in intensity much at all. If this static were from
something on our world, like radio transmissions from a nearby airport control
tower, it would only come from one direction, not everywhere. The scientists
soon realized they had discovered the cosmic microwave background radiation.
This radiation, which fills the entire Universe, is believed to be a clue to it's
beginning, something known as the Big Bang.
The image above is a Cosmic Background Explorer (COBE) image of the cosmic
microwave background, the pink and blue colors showing the tiny fluctuations in
it.

129. 129
Radio Waves
What do Radio Waves show us?
The above image shows the Carbon Monoxide (CO) gases in our Milky Way
galaxy.
Many astronomical objects emit radio waves, but that fact wasn't discovered until
1932. Since then, astronomers have developed sophisticated systems that allow
them to make pictures from the radio waves emitted by astronomical objects.
Radio telescopes look toward the heavens at
planets and comets, giant clouds of gas and
dust, and stars and galaxies. By studying the
radio waves originating from these sources,
astronomers can learn about their
composition, structure, and motion. Radio
astronomy has the advantage that sunlight,
clouds, and rain do not affect observations.
Did you know that radio
astronomy observatories
use diesel cars around the
telescopes? The ignition of
the spark plugs in
gasoline-powered cars
can interfere with radio
observations - just like
running a vacuum can
interfere with your
television reception!

130. 130