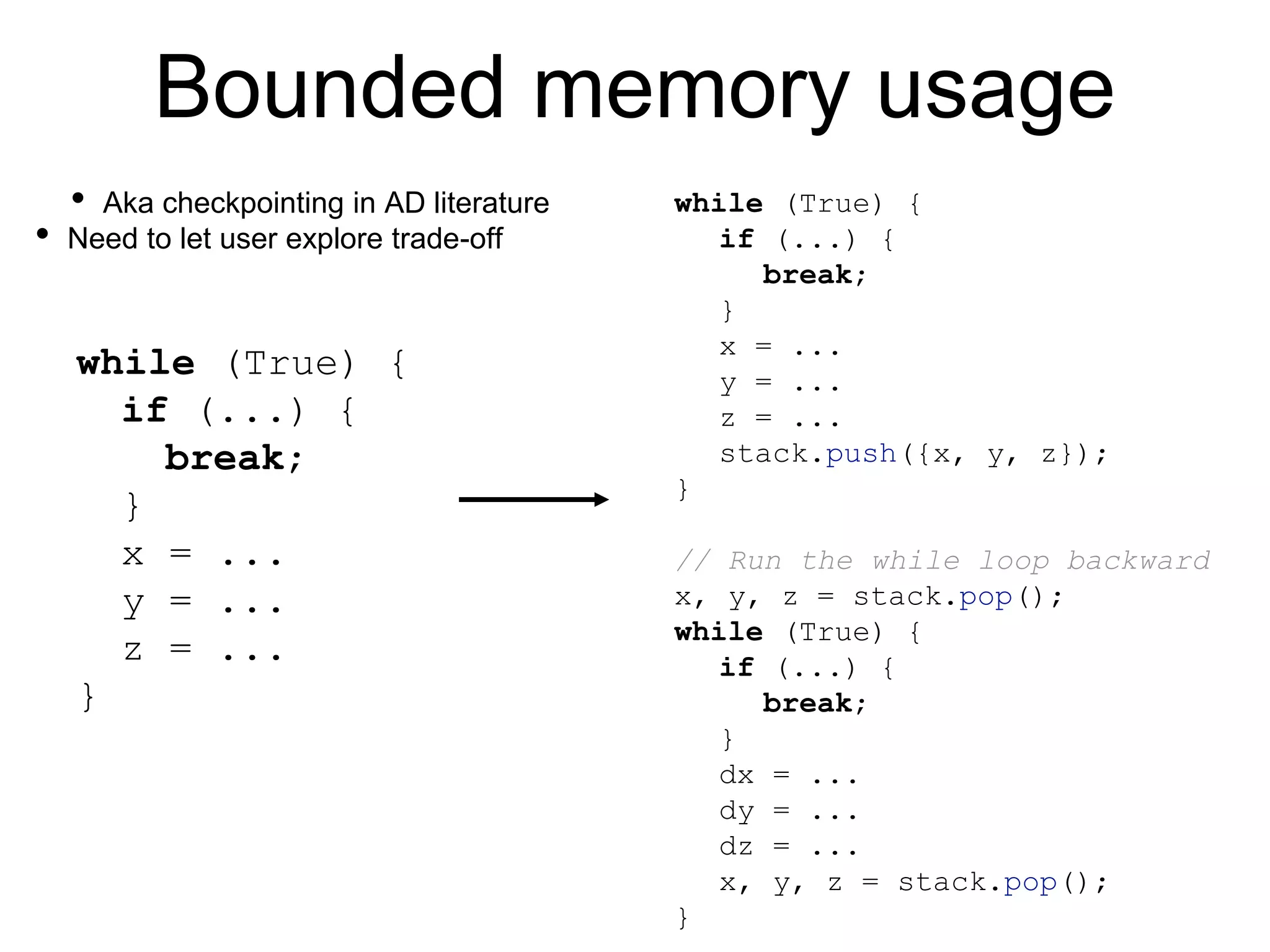
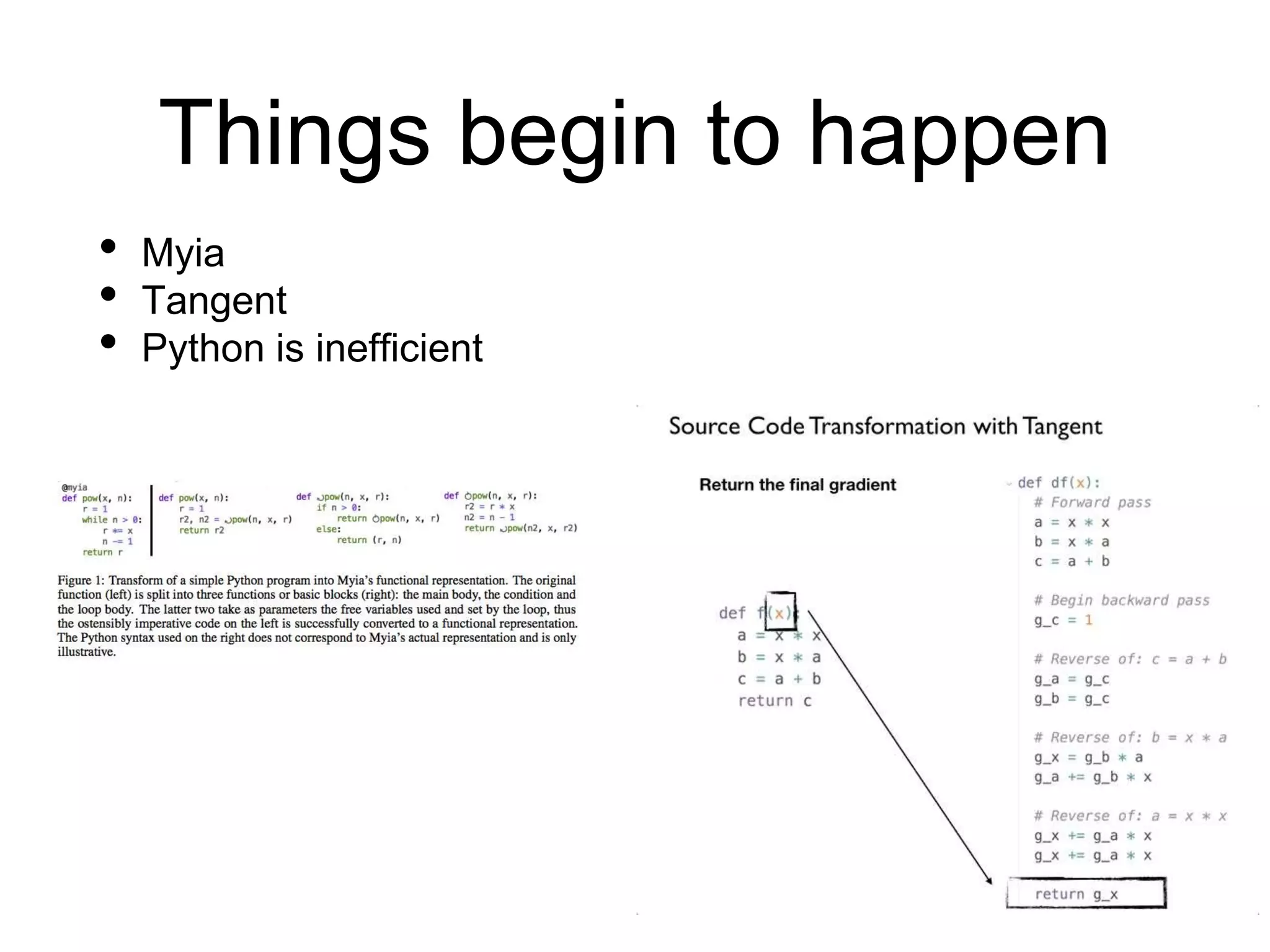
The document discusses the challenges of building an efficient automatic differentiation (autodiff) compiler. It outlines goals such as efficiency through detecting common expressions, constant folding at compile time, parallelism, bounded memory usage, and convenience without changing forward code. It also discusses handling non-differentiability, parallelism challenges, bounded memory usage through checkpointing, efficiently computing higher-order derivatives, and existing theories and implementations.

1. What do I want from my
autodiff compiler
Why is this hard?
float x = ...
// ...
float y = ...
float dydx = d(y)/d(x)
some compile-time magic here
Tzu-Mao Li

2. Goal
• Efficient
• Need to detect common expressions for multiple
derivatives (special case: reverse mode)
• Constants should fold at compile time
• Parallelism (SIMD friendly)
• Bounded memory usage
• Convenient
• Don’t need to change forward code
• Easily handle Jacobian/higher-order derivatives
• General
• Handle non-differentiability by approximation or warning

3. Theories are there
Pearlmutter and Siskind, 2008
“Reverse-Mode AD in a Functional Framework:
Lambda the Ultimate Backpropagator”
Villard and Monagan, 1998
“Automatic differentiation: an implementation in Maple”

4. Constants should fold
t6 = x + 2 * y;
t5 = 2 * x + y;
t4 = t6;
t3 = t5 + t6;
t2 = t5;
t1 = t3 + t4;
t0 = t2 + t3;
z = t0 + t1;
• PyTorch and all dynamic taping approaches fail here
• Saved by the fact that in deep learning
all linear combination follows by a nonlinearity
d(z) / d(x) == constant
d(z) / d(y) == constant

5. Parallelism
• Basically we want to write CUDA/ispc style code and
differentiate them
• Need to handle heterogenous computation
• Race condition
t6 = x + 2 * y;
t5 = 2 * x + y;
t4 = t6;
t3 = t5 + t6;
t2 = t5;
t1 = t3 + t4;
t0 = t2 + t3;
z = t0 + t1;

6. Bounded memory usage
while (True) {
if (...) {
break;
}
x = ...
y = ...
z = ...
}
while (True) {
if (...) {
break;
}
x = ...
y = ...
z = ...
stack.push({x, y, z});
}
// Run the while loop backward
x, y, z = stack.pop();
while (True) {
if (...) {
break;
}
dx = ...
dy = ...
dz = ...
x, y, z = stack.pop();
}
• Aka checkpointing in AD literature
• Need to let user explore trade-off

7. Don’t need to change forward
code
• Need a decent parser
• Or a language with strong meta programming ability e.g. Lisp,
Terra
float x = ...
// ...
float y = ...
float dydx = d(y)/d(x)
ad_float x = ...
// ...
ad_float y = ...
ad_float dydx = d(y)/d(x)
Don’t want this
Gets worse with control flow

8. Easily handle
Jacobian/higher-order
derivatives
float x = ...
float k = ...
// ...
float y = ...
float dydx = d(y)/d(x)
float d2ydxdk = d(dydx)/d(k)
• Tricky to get optimal performance
• NP-hard for arbitrary Jacobian (good heuristics exist)
• Symmetry of Hessian matrix
• Reverse-on-forward mode
• Efficient Jacobian/Hessian vector product

9. Handle non-differentiability
• e.g. Piecewise-constant function
• Users may not know that their functions are not
differentiable for certain input ranges
• Either automatically approximate or warn the users
• Numerical issues at boundaries: e.g. d/dx sqrt(x) = -
1/sqrt(x) when x->0

10. Things begin to happen
• Myia
• Tangent
• Python is inefficient