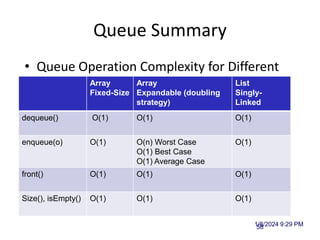
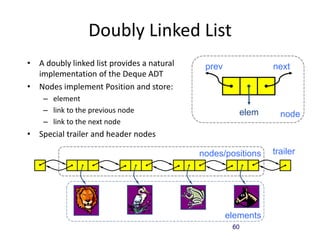
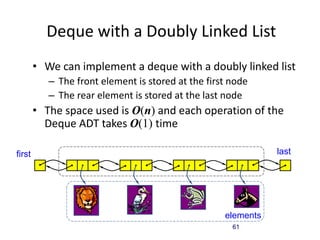
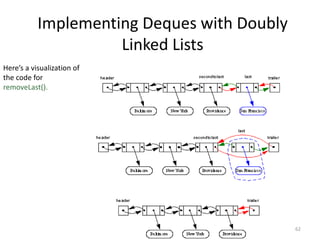
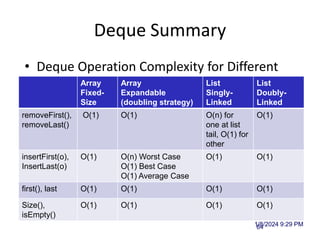
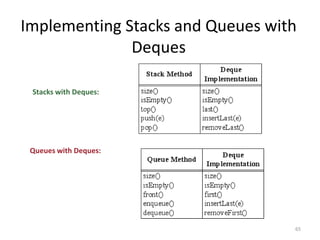
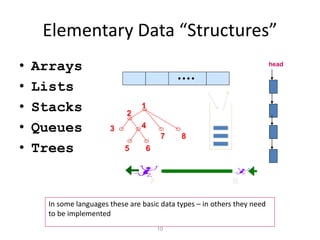
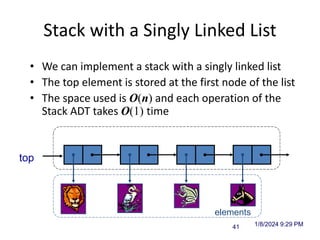
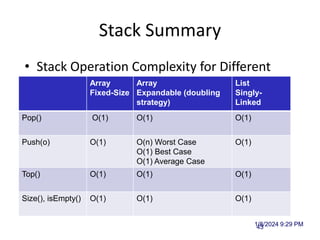
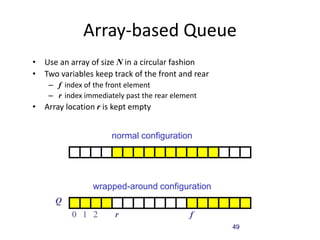
The document discusses data structures and introduces common data structures like stacks and queues. It explains that stacks follow LIFO order and have push and pop operations, while queues follow FIFO order and have enqueue and dequeue operations. Array-based and linked list implementations of stacks and queues are described, with their time and space complexities analyzed. Exceptions for invalid operations like popping an empty stack are also covered.
















![20
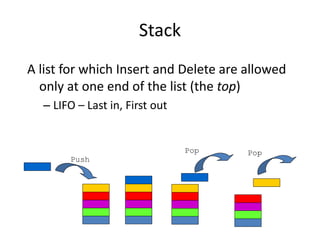
Examples
• Basic Types
– integer, real (floating point), boolean (0,1),
character
• Arrays
– A[0..99] : integer array
– A[0..99] : array of images
0 1 2 3 4 5 6 7 99
A …
2 1 3 3 2 9 9 6 10
0 1 2 99
…](https://image.slidesharecdn.com/week2-stacks-queues-240108212904-1fcf3099/85/Week2-stacks-queues-pptx-20-320.jpg)
![21
A mapping from an index set, such as
{0,1,2,…,n}, into a cell type
Objects: set of cells
Operations:
• create(A,n)
• put(A,v,i) or A[i] = v
• value(A,i)
ADT: Array](https://image.slidesharecdn.com/week2-stacks-queues-240108212904-1fcf3099/85/Week2-stacks-queues-pptx-21-320.jpg)


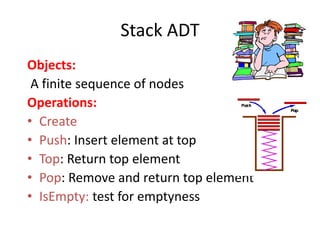


![Stacks 28
Parentheses Matching
• Each “(”, “{”, or “[” must be paired with a
matching “)”, “}”, or “[”
– correct: ( )(( )){([( )])}
– correct: ((( )(( )){([( )])}
– incorrect: )(( )){([( )])}
– incorrect: ({[ ])}
– incorrect: (](https://image.slidesharecdn.com/week2-stacks-queues-240108212904-1fcf3099/85/Week2-stacks-queues-pptx-28-320.jpg)
![Stacks 29
Parentheses Matching Algorithm
Algorithm ParenMatch(X,n):
Input: An array X of n tokens, each of which is either a grouping symbol, a
variable, an arithmetic operator, or a number
Output: true if and only if all the grouping symbols in X match
Let S be an empty stack
for i=0 to n-1 do
if X[i] is an opening grouping symbol then
S.push(X[i])
else if X[i] is a closing grouping symbol then
if S.isEmpty() then
return false {nothing to match with}
if S.pop() does not match the type of X[i] then
return false {wrong type}
if S.isEmpty() then
return true {every symbol matched}
else
return false {some symbols were never matched}](https://image.slidesharecdn.com/week2-stacks-queues-240108212904-1fcf3099/85/Week2-stacks-queues-pptx-29-320.jpg)

![Array-based Stack
• A simple way of
implementing the
Stack ADT uses an
array
• We add elements
from left to right
• A variable keeps track
of the index of the
top element
S
0 1 2 t
…
Algorithm size()
return t + 1
Algorithm pop()
if empty() then
throw EmptyStackException
else
t = t - 1
return S[t + 1]](https://image.slidesharecdn.com/week2-stacks-queues-240108212904-1fcf3099/85/Week2-stacks-queues-pptx-31-320.jpg)
![32
Array-based Stack (cont.)
• The array storing the
stack elements may
become full
• A push operation will
then throw a
FullStackException
– Limitation of the
array-based
implementation
– Not intrinsic to the
Stack ADT
S
0 1 2 t
…
Algorithm push(o)
if t = S.length - 1 then
throw FullStackException
else
t = t + 1
S[t] = o](https://image.slidesharecdn.com/week2-stacks-queues-240108212904-1fcf3099/85/Week2-stacks-queues-pptx-32-320.jpg)

![Growable Array-based Stack
• In a push operation, when the
array is full, instead of
throwing an exception, we
can replace the array with a
larger one
• How large should the new
array be?
– incremental strategy: increase
the size by a constant c
– doubling strategy: double the
size
Algorithm push(o)
if t = S.length - 1
then
A = new array of
size …
for i = 0 to t do
A[i] = S[i]
S = A
t = t + 1
S[t] = o](https://image.slidesharecdn.com/week2-stacks-queues-240108212904-1fcf3099/85/Week2-stacks-queues-pptx-34-320.jpg)




![39
Array-based Stack in C++
template <typename Object>
class ArrayStack {
private:
int capacity; // stack capacity
Object *S; // stack array
int top; // top of stack
public:
ArrayStack(int c) {
capacity = c;
S = new Object[capacity];
t = –1;
}
bool isEmpty()
{ return (t < 0); }
Object pop()
{
if(isEmpty())
throw EmptyStackException
(“Access to empty stack”);
return S[t--];
}
// … (other functions omitted)](https://image.slidesharecdn.com/week2-stacks-queues-240108212904-1fcf3099/85/Week2-stacks-queues-pptx-39-320.jpg)





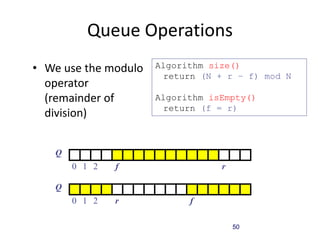
![51
Queue Operations (cont.)
Algorithm enqueue(o)
if size() = N - 1 then
throw FullQueueException
else
Q[r] = o
r = (r + 1) mod N
• Operation enqueue throws an
exception if the array is full
• This exception is
implementation-dependent
Q
0 1 2 r
f
Q
0 1 2 f
r](https://image.slidesharecdn.com/week2-stacks-queues-240108212904-1fcf3099/85/Week2-stacks-queues-pptx-51-320.jpg)
![52
Queue Operations (cont.)
• Operation dequeue
throws an exception
if the queue is
empty
• This exception is
specified in the
queue ADT
Algorithm dequeue()
if isEmpty() then
throw EmptyQueueException
else
o = Q[f]
f = (f + 1) mod N
return o
Q
0 1 2 r
f
Q
0 1 2 f
r](https://image.slidesharecdn.com/week2-stacks-queues-240108212904-1fcf3099/85/Week2-stacks-queues-pptx-52-320.jpg)