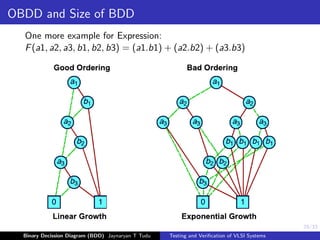
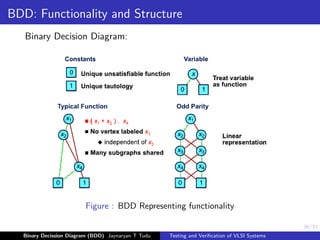
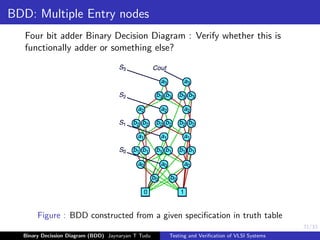
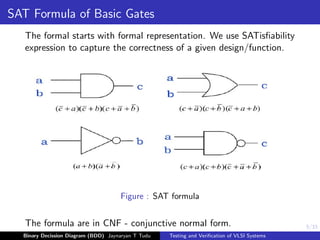
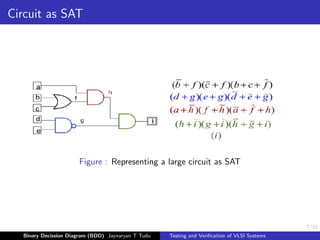
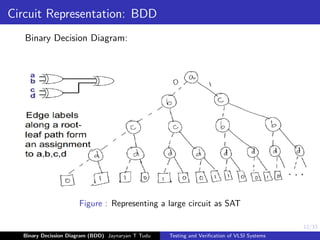
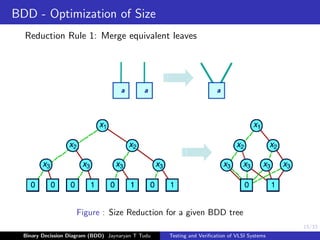
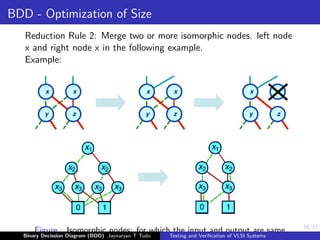
This document discusses binary decision diagrams (BDDs) and their use in formal verification of VLSI systems. It describes how BDDs can be constructed to represent Boolean functions and circuits. The ordering of variables in a BDD impacts its size, and ordered BDDs provide a canonical representation of functions. BDDs can be used for equivalence checking and other formal verification tasks by comparing the structure of BDDs representing different functions or circuits. Well-ordered BDDs provide an efficient way to perform tasks like validity checking, satisfiability checking, and implication checking on circuit representations.

1. 1/33
Testing and Verification of VLSI Systems
Binary Decission Diagram (BDD)
Jaynaryan T Tudu
Indian Institute of Technology Tirupati, India
31st Jan, 2023
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

2. 3/33
Verification Flow
Figure : Verification flow of the possible approaches
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

3. 4/33
Formal Verification Methodology
Create a formal model for some system of interest:
Hardware
Communication Protocol
Software - specifically concurrent software
Describe formally a specification that we desire the model to
satisfy
Check whether the model satisfies the specification
- Theorem proving
- Model checking
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

4. 5/33
SAT Formula of Basic Gates
The formal starts with formal representation. We use SATisfiability
expression to capture the correctness of a given design/function.
Figure : SAT formula
The formula are in CNF - conjunctive normal form.
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

5. 6/33
Derivation of SAT and CNF
The boolean expression of the:
a → b is a + b
Example 1: Deriving CNF of c = a + b
if c is true, then at least one of its inputs a or b is true
if c is false, then both its inputs a and b are false
(c → (a + b)).(c → a.b)
(c + (a + b)).(c + (a.b))
(c + a + b).(c + (a).(c + b))
Example 2: Deriving CNF for r ↔ (p + q)
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

6. 7/33
Circuit as SAT
Figure : Representing a large circuit as SAT
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

7. 8/33
Circuit as SAT: XOR Gate
How to verify using simulation? How to verify using formal
method?
Figure : XOR gate using NAND
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

8. 9/33
Circuit as SAT Formal Verification
Transformation of formulae to the specification of circuit
Apply mathematical reasoning and axioms
Figure : Mathematical Proof of correctness
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

9. 10/33
Formal Verification Techniques
Deductive verification (theorem proving)
Axiom based proving.
Model Checking
Symbolic algorithm using binary decission diagram
Equivalence checking
Check whether two circuit are equivalent
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

10. 11/33
Circuit Representation
As Boolean function
As Binary decission diagram
A boolean function with n variable:
F : {0, 1}n → 0, 1
The function can be further expressed with n-1 variables.
Fx1 (x2.....xn) = F(1, x2, x3, ......xn)
Fx0
1
(x2....xn) = F(0, x2, x3, ......xn)
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

11. 12/33
Circuit Representation: BDD
Binary Decision Diagram:
Figure : Representing a large circuit as SAT
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

12. 13/33
Binary Decision Diagram (BDD)
How to construct a BDD from a given specification of design/ckt?
Specification: Truth table or Written in HDL - functional
Figure : BDD constructed from a given specification in truth table
Description of BDD: Vertex represent Decision variable, Greenline
edge for value 0 and Redline edge for value 1, and leaf node for
function value. A Path is from root to leaf.
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

13. 14/33
BDD: Variable Ordering
Examine for ordering of the variable, does it matter?
Example:
Figure : The variable ordering rule to be followed
Assign total ordering to variables: x1 < x2 < x3
Variable must appear in ascending order along all the paths.
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

14. 15/33
BDD - Optimization of Size
Reduction Rule 1: Merge equivalent leaves
Figure : Size Reduction for a given BDD tree
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

15. 16/33
BDD - Optimization of Size
Reduction Rule 2: Merge two or more isomorphic nodes. left node
x and right node x in the following example.
Example:
Figure : Isomorphic nodes: for which the input and output are same
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

16. 17/33
BDD Optimization
Rule 3: Eliminate Redundant Nodes: Two consecuting nodes
connected with dual edges (0 and 1) can be merged
Example:
Figure : X2 is redundant of X3 and X3 in left is redundant to 0
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

17. 18/33
Using BDD in Verification
One use we have seen on how BDD can be used to determine
SAT assignment
Can we use this for formal equivalence checking?
Can we check that two circuits with same functionality will
have some properties to say that they are equivalent or having
same functionality? (we are not so much concerned about
structure.)
Can the same functionality a circuit may leads to two or more
different kind of BDD?
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

18. 19/33
Using BDD in Verification: Variable Ordering
Example: Are these two diagram represen the same functionality?
Figure : Two BDD with different looks having same functionality
How do we ensure they are indeed same?
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

19. 20/33
Using BDD in Verification: Variable Ordering
Example: Are these two diagram represen the same functionality?
Figure : Two BDD with different looks having same functionality
How do we ensure they are indeed same?
Ans: can we find out one-to-one mapping among variables such
that the traversed path remain similar?
Example: a <=> b
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

20. 21/33
Using BDD in Verification: Variable Ordering
Do this Example : a.(b + c)
Figure : Two differently looking spcifications for above expression
Can we use BDD to say that they are same?
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

21. 22/33
OBDD: Ordered Binary Decision Diagram OBDD
Therefore, order of the variable can leads to differently looking
BDD.
Also, we have seen for the same variable order, we may get
different BDD! (optimized vs unoptimized)
Figure : BDD constructed from a given specification
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

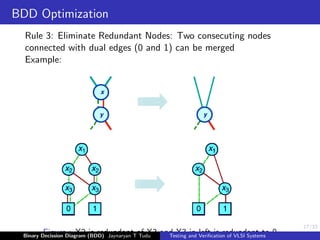
22. 23/33
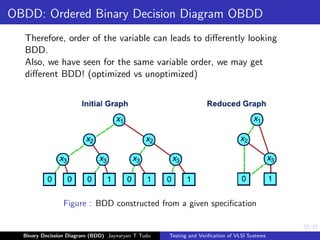
OBDD: Ordered Binary Decision Diagram OBDD
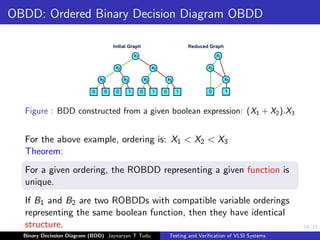
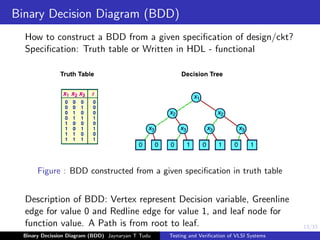
Figure : BDD constructed from a given boolean expression: (X1 + X2).X3
Ordered BDD:
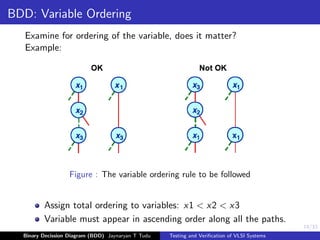
Let [x1, ..., xn] be an ordered list of variables without duplicates;
A BDD B has an ordering [x1, ..., xn] if
1. all variables of B occur in [x1, ..., xn]; and
2. if xj follows xi on a path in B then j > i
An ordered BDD (OBDD) is a BDD which has an ordering for some
list of variables.
The orderings of two OBBDs B and B’ are compatible if there are
no variables x, y such that: x is before y in the ordering for B, and y
is before x in the ordering for B’
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

23. 24/33
OBDD: Ordered Binary Decision Diagram OBDD
Figure : BDD constructed from a given boolean expression: (X1 + X2).X3
For the above example, ordering is: X1 < X2 < X3
Theorem:
For a given ordering, the ROBDD representing a given function is
unique.
If B1 and B2 are two ROBDDs with compatible variable orderings
representing the same boolean function, then they have identical
structure.
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

24. 25/33
Graph Isomorphism, ROBDD and Linear Complexity
Canonical representation of boolean function:
Theorem
For a given variable ordering, two functions are equivalent if and
only if graphs’ isomorphic can be tested in linear time. In
otherway: graph morphism for ROBDD for the same order can be
tested in linear time. (true for canonical representation.)
Exercise: Ordered BDD are same as the canonical boolean
expression!
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

25. 26/33
OBDD and Size of BDD
- We have seen, order of variables do not have any impact on
functionality (needs an equivalence checking).
- Does the order of variable impacts the size of OBDD and the
ROBDD?
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

26. 27/33
OBDD and Size of BDD
- We have seen, order of variables do not have any impact on functionality
(needs an equivalence checking).
- Does the order of variable impacts the size of OBDD and the ROBDD?
Example:
(a.b + c.d), construct OBDD, and ROBDD for the order
a < b < c < d and a < c < b < d
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

27. 28/33
OBDD and Size of BDD
- We have seen, order of variables do not have any impact on functionality
(needs an equivalence checking).
- Does the order of variable impacts the size of OBDD and the ROBDD?
Example:
(a.b + c.d), construct OBDD, and ROBDD for the order
a < b < c < d and a < c < b < d
Figure : ROBDDs for two different orders of the same
specification/expression
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

28. 29/33
OBDD and Size of BDD
One more example for Expression:
F(a1, a2, a3, b1, b2, b3) = (a1.b1) + (a2.b2) + (a3.b3)
Figure : BDD constructed from a given specification in truth table
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

29. 30/33
BDD: Functionality and Structure
Binary Decision Diagram:
Figure : BDD Representing functionality
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

30. 31/33
BDD: Multiple Entry nodes
Four bit adder Binary Decision Diagram : Verify whether this is
functionally adder or something else?
Figure : BDD constructed from a given specification in truth table
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

31. 32/33
Usefulness of Canonical Representation
Absence of redundant variables: A boolean function f does
not depend on an input variable x if no nodes occur for x in
the ROBDD for f.
Semantic equivalence: Check f ≡ g by checking whether or
not the ROBDDs for f and g have identical structure.
Validity: Check if the BDD is identical to the one with just
the terminal node 1 and nothing else.
Satisfiability: Check if the BDD is not identical to the one
with just the terminal node 0 and nothing else.
Implication. Check if by for all x, f(x) → g(x) by checking
whether or not the ROBDD for f . g is constant 0.
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems

32. 33/33
Thank you
Formal verification Vs Simulation!
Thank You!
Binary Decission Diagram (BDD) Jaynaryan T Tudu Testing and Verification of VLSI Systems