Downloaded 21 times
Uploaded byVisionGEOMATIQUE2014
MACHINE LEARNING FOR SATELLITE-GUIDED WATER QUALITY MONITORING
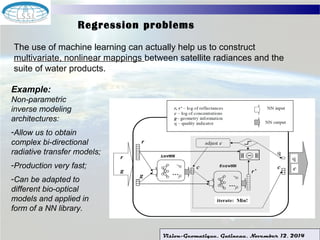
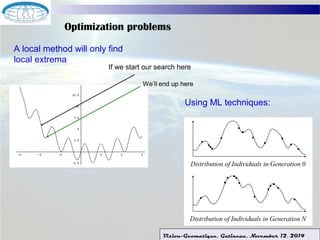
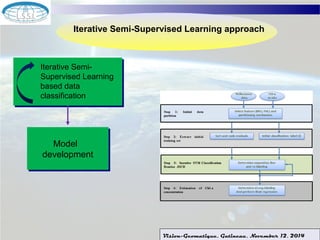
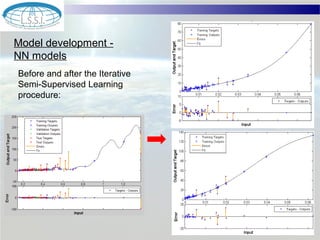
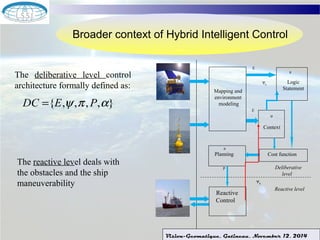
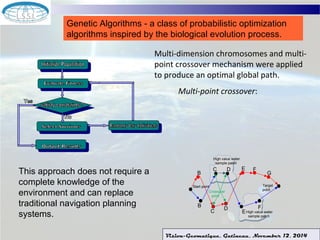
The document discusses using machine learning techniques for satellite-guided water quality monitoring. It covers using machine learning algorithms to automatically develop empirical models from multimodal satellite and field data sets. Machine learning can help construct nonlinear mappings between satellite measurements and water quality products and optimize in-situ data collection through mission planning. Experimental results are shown applying these techniques to map water quality metrics like chlorophyll-a and total suspended solids using MODIS satellite images of Lake Winnipeg.
More Related Content
Similar to MACHINE LEARNING FOR SATELLITE-GUIDED WATER QUALITY MONITORING
More from VisionGEOMATIQUE2014
MACHINE LEARNING FOR SATELLITE-GUIDED WATER QUALITY MONITORING
- 1. MACHINE LEARNING FOR SATELLITE-GUIDED WATER QUALITY MONITORING Marek B. Zaremba Laboratoire de Systèmes Spatiaux Intelligents (LSSI) Département d’informatique et d’ingénierie Université du Québec en Outaouais Gatineau, Canada Vision-Geomatique, Gatineau, November 12, 2014
- 2. OOUUTTLLIINNEE 1. MachineLearning 2. Problems solved 3. Automated model development: multimodal data sets 4. Mission planning and optimization 5. Final Comments Vision-Geomatique, Gatineau, November 12, 2014
- 3. 1. MACHINE LEARNING Machine learning is a sub-field of artificial intelligence that is concerned with the design and development of algorithms that allow computers to learn the behavior of data sets empirically. Vision-Geomatique, Gatineau, November 12, 2014 What is Machine Learning? A major focus of machine-learning research is to produce (induce) empirical models from data automatically. WHY? This approach is usually used because of the absence of adequate and complete theoretical models. Can’t you do anything right?
- 4. Machine Learning Algorithms About 2500 years ago Democritus wrote: “Fools can learn from their own experience; the wise learn from the experience of others.” Machine learning task of inferring a function from labeled training data. Vision-Geomatique, Gatineau, November 12, 2014 Unsupervised learning Vector Quantization Self-Organizing Maps EM algorithm Hierarchical clustering K-means algorithm Fuzzy clustering etc. Supervised learning As well as: Reinforcement learning Transductive learning Deep learning
- 5. Supervised learning NeuralNetworks They learn complex nonlinear input-output Backpropagation Autoencoders Hopfield networks Boltzmann machines Restricted Boltzmann Machines Spiking neural networks etc. Support Vector Machines relationships and adapt themselves to the data, using sequential training procedures. SVMs map the training data into a higher-dimensional feature space via kernel mapping, and construct a separating hyperplane with a maximum error margin. Vision-Geomatique, Gatineau, November 12, 2014 Linear classifiers Fisher's linear discriminant Logistic regression Multinomial logistic regression Naive Bayes classifier Perceptron
- 6. 2. PROBLEMS SOLVED Learning Algorithms – which are the best? The No Free Lunch (NFL) theorem (Wolpert and Macready, 1995) has shown that learning algorithms cannot be universally good. Matching algorithms to problems gives higher average performance than does applying a fixed algorithm to all. Hence: Experience with a broad range of techniques is the best insurance for solving arbitrary new problems General classes of problems: Vision-Geomatique, Gatineau, November 12, 2014 Classification Regression Optimization
- 7. Vision-Geomatique, Gatineau, November12, 2014 Classification problems Supervised and unsupervised Ex. Water/Land cover classification
- 8. Regression problems Theuse of machine learning can actually help us to construct multivariate, nonlinear mappings between satellite radiances and the suite of water products. Vision-Geomatique, Gatineau, November 12, 2014 Example: Non-parametric inverse modeling architectures: -Allow us to obtain complex bi-directional radiative transfer models; -Production very fast; -Can be adapted to different bio-optical models and applied in form of a NN library.
- 9. Optimization problems Ifwe start our search here Vision-Geomatique, Gatineau, November 12, 2014 A local method will only find local extrema Using ML techniques:
- 10. 3. AUTOMATED MODELDEVELOPMENT: MULTIMODAL DATA SETS 140 120 100 80 60 40 20 0 Chlorophyll-a Distribution -1 0 1 2 3 4 5 6 Chlorophyll-a concentration mg/m 3 MCI-MERIS Vision-Geomatique, Gatineau, November 12, 2014 Case study Chlorophyll-a detection -Using data from satellites and field spectrometers Linear model (R2 = 0.679):
- 11. Parametric models Examples: Models Non-parametric models - data-driven models obtained using the statistical learning process. Neural Network technology: Vision-Geomatique, Gatineau, November 12, 2014
- 12. The problem … Biased (statistics systematically different from the population parameter) and non-ergodic (distribution parameters vary in time) data sets Biases are ubiquitous. With fusion of multiple datasets bias is often an issue (very relevant for climate variables). Yet, we typically need to fuse multiple datasets to construct long-term time series and/or improve global coverage. If the biases are not corrected before data fusion we introduce further problems, such as spurious trends, leading to the possibility of unsuitable policy decisions. So what can we do about this? .... we do not have a theoretical explanation (The Earth system is so complex, with many interacting processes, and often the instruments are also complex, this is not always possible to theoretically understand the cause of the bias and data issues from first principles).
- 13. Iterative Semi-Supervised Learningapproach Vision-Geomatique, Gatineau, November 12, 2014 Iterative Semi- Supervised Learning based data classification Model development Model development
- 14. Model development - NN models Before and after the Iterative Semi-Supervised Learning procedure:
- 15. 4. MISSION PLANNINGAND OPTIMIZATION Objective: Optimization of the in-situ data acquisition process through the planning of an optimal ship trajectory. The path planning system generates an optimal path with the goal of maximizing the number and the value of the collected samples during the acquisition mission. The acquisition mission can be varied depending on the strategy applied to collect the samples for different water pollutants (Chl-a, TSS, DOC, …) : Maximum gradient following strategy Maximum concentration areas Uniform coverage strategy Any strategy can be represented by an objective function. æ å NJ = +å +å C V / N t D i J The strategies can be applied depending on the surrounding environment and the data acquisition mission constraints. ö ÷ ÷ø ç çè = = = i K S K J S J 1 1 1
- 16. Broader context ofHybrid Intelligent Control ψ Mapping and environment modeling α Planning P E Context Reactive Control E ΨE π Logic Statement Cost function Deliberative level Reactive level ΨR The deliberative level control architecture formally defined as: DC ={E,y ,p ,P,a} The reactive level deals with the obstacles and the ship maneuverability Vision-Geomatique, Gatineau, November 12, 2014
- 17. Genetic Algorithms approach Classes of Search Techniques: GAs use different: Representations (chromosomes) Mutation and Crossover mechanisms Fitness functions Vision-Geomatique, Gatineau, November 12, 2014
- 18. Genetic Algorithms -a class of probabilistic optimization algorithms inspired by the biological evolution process. Multi-dimension chromosomes and multi-point crossover mechanism were applied to produce an optimal global path. Multi-point crossover: High value water sample patch B C D E Start point D E G Target point F High value water sample patch B C F Crossover point This approach does not require a complete knowledge of the environment and can replace traditional navigation planning systems. Vision-Geomatique, Gatineau, November 12, 2014
- 19. EXPERIMENTAL RESULTS Satelliteimages (MODIS) of Lake Winnipeg TSS Map MCI Map Vision-Geomatique, Gatineau, November 12, 2014
- 20. TSS and Chl-a(maximum values) samples acquisition longitude latitude Value -97.071594 52.271004 0.3949 -97.15443 52.271156 0.3678 -97.0877 52.163826 0.4037 -96.9688 51.998085 0.4001 -96.94884 51.884686 0.4083 -97.10551 51.87565 0.4532 -97.17112 51.886684 0.4526 -97.17112 51.886684 0.4378 -97.19144 51.804962 0.4324 -97.25087 51.705112 0.4360 -97.27605 51.62972 0.4971 -97.27722 51.555775 0.6226 -97.27228 51.47804 0.6288 -97.258446 51.456432 0.6196 -97.213425 51.470726 0.6044 -97.187546 51.485546 0.5692 -97.18434 51.53722 0.5521 -97.22941 51.522934 0.5597 -97.19398 51.577347 0.3957 -97.13055 51.624245 0.5948 -97.10014 51.69328 0.3663 -97.040436 51.83706 0.4298 -97.08387 51.95991 0.4200 -97.13075 52.102375 0.3001 -97.14458 52.231052 0.4037 -97.08629 52.273468 0.3931 Vision-Geomatique, Gatineau, November 12, 2014
- 21. 5. FINAL COMMENTS Vision-Geomatique, Gatineau, November 12, 2014 Machine learning: • Focuses on problems that otherwise cannot be solved; • A tool of fighting complexity; • Employs cognitive properties of intelligence: generalization, attention focusing, combinatorial search, … Extremely useful for automatic decision making. Very well suited for monitoring environmental phenomena. But: Use of context is necessary for identifying complex patterns. No single technique/model is suited for all problems. “All models are wrong … … some models are useful” George Box
- 22.
Editor's Notes
- #5 Dimensionality increase - two important consequences. First, higher dimensional space is mostly empty. This implies that a high dimensional data set can be projected to a lower dimensional subspace without losing significant information in terms of separability among different classes. The second consequence is that normally distributed data will have a tendency to concentrate in the tails; Making density estimation more difficult. Local neighborhoods are almost surely empty, requiring the bandwidth of estimation to be large and producing the effect of losing detailed density estimation.
- #6 Dimensionality increase - two important consequences. First, higher dimensional space is mostly empty. This implies that a high dimensional data set can be projected to a lower dimensional subspace without losing significant information in terms of separability among different classes. The second consequence is that normally distributed data will have a tendency to concentrate in the tails; Making density estimation more difficult. Local neighborhoods are almost surely empty, requiring the bandwidth of estimation to be large and producing the effect of losing detailed density estimation.
- #9 Dimensionality increase - two important consequences. First, higher dimensional space is mostly empty. This implies that a high dimensional data set can be projected to a lower dimensional subspace without losing significant information in terms of separability among different classes. The second consequence is that normally distributed data will have a tendency to concentrate in the tails; Making density estimation more difficult. Local neighborhoods are almost surely empty, requiring the bandwidth of estimation to be large and producing the effect of losing detailed density estimation.
- #13 Dimensionality increase - two important consequences. First, higher dimensional space is mostly empty. This implies that a high dimensional data set can be projected to a lower dimensional subspace without losing significant information in terms of separability among different classes. The second consequence is that normally distributed data will have a tendency to concentrate in the tails; Making density estimation more difficult. Local neighborhoods are almost surely empty, requiring the bandwidth of estimation to be large and producing the effect of losing detailed density estimation.
- #20 Whiter regions denote high TSS index. In MCI, the whiter zones denote a high clorofyll concentration. The border between the white regions and the darker gray regions represent maximum gradient samples.
- #21 This figure shows the resulting path for the acquisition of TSS samples. The acquisition mission resulted in 26 samples along a 220.5 km long path.