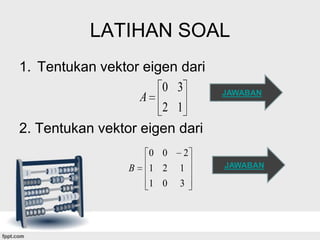
Dokumen ini membahas tentang konsep vektor eigen dan nilai eigen dari suatu matriks, termasuk definisi, cara menentukan nilai dan vektor eigen, serta contoh soal dan penyelesaiannya. Diberikan penjelasan tentang persamaan karakteristik dan ruang eigen yang digunakan untuk menemukan basis ruang eigen. Terdapat juga latihan soal terkait untuk memperdalam pemahaman.

1. VEKTOR KARAKTERISTIK
Kelompok 21:
Dyas Arintya P. (120210101086)
Afi Latul Laili (120210101115)

2. Definisi :
Jika A adalah matriks n x n, maka vektor taknol x
di dalam Rn dinamakan vektor eigen(eigenvektor)
dari A jika Ax adalah kelipatan skalar dari x; yakni:
Ax = λx
A : vektor berukuran n x n
λ : skalar riil yang memenuhi
persamaan, disebut nilai eigen
x : vektor eigen yang bersesuaian
dengan λ

3. Cara menentukan nilai eigen dari A :
Untuk mencari nilai eigen dari matrik A yang
berukuran n x n yang memenuhi persamaan :
Ax = λx dapat ditulis sebagai : Ax = λIx atau
ekivalen : (λI – A)x = 0
Sistem persamaan tersebut memiliki nilai bukan
nol (singular), jika dan hanya jika :
Ini disebut sebagai persamaan
karakteristik
(polinomial dalam λ)

4. Cara menentukan vektor eigen dari A :
 Banyaknya nilai eigen maksimal n buah.
Untuk setiap nilai eigen dapat dicari ruang solusi
untuk x dengan memasukkan nilai eigen ke
dalam persamaan : (λI – A)x =0
 Ruang solusi yang diperoleh disebut : ruang
eigen. Dari ruang eigen yang bersesuaian
dengan nilai eigen tertentu dapat dicari minimal
sebuah basis ruang eigen yang saling bebas
linier.
Vektor eigen yang berhubungan
dengan λ adalah vektor-vektor tidak
nol dalam ruang eigen.

5. Contoh soal :
1. Buktikan vektor x
A
3 0
8
1
1
adalah vektor eigen dari
2
dan tentukan nilai eigennya!
Jawab :
Untuk membuktikannya dilakukan dengan cara
mengali-kan matrik dengan vektor, sehingga
diperoleh hasil kelipatan dari vektor iatu sendiri.
Ax
3
8
0
1
3
1 2
6
3
1
2
vektor eigen
nilai eigen

6. 2. Carilah vektor eigen dari :
4 1
A
2 1
Jawab :
1 0
0 1
det( I A)
(
4)(
2
(
1) 2 0
5
6 0
3)(
1
3,
2) 0
2
2
4
2
1
1
4
2
1
1
0

7. Untuk
( I
3 substitusikan ke persamaan
1
A) x
1 1
0
x1
0
2 2 x2
x1
x2
2 x1
0
2 x2
Misal x1
x1
0
x2
x1
s, maka x 2
x2
s
Jadi vektor eigen yang bersesuaian dengan
x
s
s
s
1
1
1
3 adalah

8. Untuk
( I
2 substitusikan ke persamaan
1
A) x
0
2 1 x1
2 1 x2
2 x1
x2
2 x1
2 x2
Misal x1
0
0
2 x1
0
2 x1
s, maka x 2
x2
x2
2s
Jadi vektor eigen yang bersesuaian dengan
x
s
2s
s
1
2
1
2 adalah

9. 3
3. Carilah vektor eigen dari : A
2 0
2
3
0
0
Jawab :
1 0 0
0 1 0
3 2 0
2 3 0
0
0
3)(
5) (4
20) 0
35
25 0
5)(
5) 0
det( I A)
(
3)(
3
(
11
2
1)(
1
1,
2
5
2
0 0 1
0
5
0 5
3
2
3
0
0
0
0
5

10. Untuk
( I
1 substitusikan ke persamaan
1
A) x
0
2
2
0
2
2
0
2 x1
2 x2
0
x1
x2
2 x1
2 x2
0
x1
x2
4 x3
0
Misal x1
0
0
4
x3
x1
x2
x3
0
0
s, maka x 2
s, serta x 3
0
Jadi, vektor eigen yang bersesuaian dengan
x
s
s
0
1
s 1
0
1 adalah

11. Untuk
( I
1
5 substitusikan ke persamaan
A) x
0
2
2
0
x1
2
0
2
0
0
0
x2
x3
0
2 x1
2 x2
0
x1
x2
2 x1
2 x2
0
x1
x2
Misal x1
s, maka x 2
s, serta x 3
t
Jadi, vektor eigen yang bersesuaian dengan
s
x
s
t
1
s
1
0
0
t 0
1
5 adalah

12. LATIHAN SOAL
1. Tentukan vektor eigen dari
A
0 3
2 1
JAWABAN
2. Tentukan vektor eigen dari
0 0
B
2
1 2
1
1 0
3
JAWABAN

13. 1. Vektor eigen dari matriks A
det( I A)
1 0
0 1
(
1) 6 0
2
6 0
3)( 2) 0
3, 2
2
(
1
0 3
2 1
0 3
2 1
2
3
0
1

14. Untuk
( I
3 substitusikan ke persamaan
1
A) x
0
3 x1
2 x2
3
2
3 x1
3x2
2 x1
0
0
2 x2
Misal x1
x1
0
x2
x1
s, maka x 2
x2
s
Jadi vektor eigen yang bersesuaian dengan
x
s
s
s
1
1
1
3 adalah

15. Untuk
( I
2
2
1
A) x
2 substitusikan ke persamaan
0
3 x1
3 x2
0
2 x1
3x2
0
2 x1
3x2
2 x1
3x2
0
2 x1
3x2
2
Misal x1 s, maka x 2
s
3
Jadi vektor eigen yang bersesuaian dengan
x
s
2
s
3
s
1
2
3
1
2 adalah
BACK

16. 2. Vektor
det( I
(
2
(
eigen
1 0 0
0 1 0
0 0 1
A)
2)(
3) ( 2(
2 )(
3) 2
3
3
2
2
3
5
2
8
(
1
2
1)( 2) 2
1, 2 2
6
4 0
0
B
0 0
1 2
1 0
dari
0 0
1 2
1 0
2
1
3
2)) 0
4 0
2
4 0
2
1
3
0
1
1
2
0
2
1
3
0

17. Untuk
( I
1
1
1
x1
1
1 substitusikan ke persamaan
A) x
0
0
2
1
0
2 x3
x1
x2
x1
2 x3
Misal x3
1
2
x1
x2
x3
0
x1
x3
0
0
0
2 x3
x2
x1
s, maka x1
x1
x3
2 x3
2 s, serta x 2
s
Jadi, vektor eigen yang bersesuaian dengan
x
2s
s
s
s
2
1
1
1 adalah

18. Untuk
( I
2
1
1
2 x1
2 substitusikan ke persamaan
1
A) x
0
0
0
2 x3
0
2
x1
1
1
x2
x3
0
0
x1
x3
x1
x3
0
x1
x3
x1
x3
0
x1
x3
Misal x3
s, maka x1
s, serta x 2
t
Jadi, vektor eigen yang bersesuaian dengan
s
x
t
s
1
s 0
1
0
t 1
0
1 adalah

19. Sekian
Terimakasih. . .