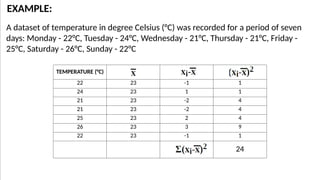
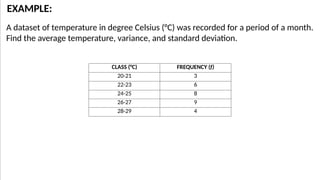
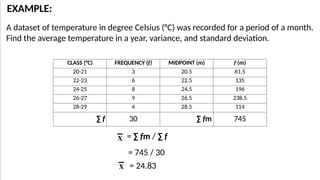
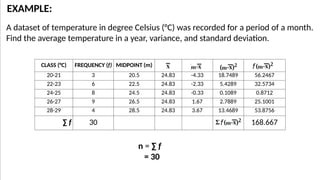
The document discusses measures of variability, specifically variance and standard deviation, explaining how they quantify the spread of data from the mean. It details the calculation methods for both grouped and ungrouped data, including formulas and examples using temperature data recorded over specific periods. The document emphasizes the efficiency of calculating variance and standard deviation for grouped data compared to ungrouped data.

1. MEASURES OF
VARIABILITY/DISPERSION
VARIANCE
&
STANDARD DEVIATION

2. STANDARD DEVIATION
Standard deviation is also a measure
of how spread out a set of data from
their mean or average value. It is
calculated by finding the square root
of the variance.
VARIANCE
Variance is a measure of how spread
out a set of data from their mean or
average value. Also known as
squared deviation. It is calculated by
finding the average of the squared
differences between each data point
and the mean.
DEFINITION

3. GROUPED DATA
Grouped data is a set of data that
has been organized into intervals
or classes. To calculate variance
and standard deviation for grouped
data, we use formulas that involve
finding the midpoint of each
interval and the frequency of data
points within each interval. This
process is more efficient than for
ungrouped data.
UNGROUPED DATA
Ungrouped data is a set of raw data
without any organization. To
calculate variance and standard
deviation for ungrouped data, we use
formulas that involve finding the
mean and the difference between
each data point and the mean. This
process can be time- consuming for
large datasets.
DEFINITION

4. UNGROUPED DATA

5. VARIANCE
FORMULA
STANDARD DEVIATION
N
N
N
N

6. = (22 + 24 + 21 + 21 + 25 + 26 + 22)/7
A dataset of temperature in degree Celsius (°C) was recorded for a period of seven
days: Monday - 22°C, Tuesday - 24°C, Wednesday - 21°C, Thursday - 21°C, Friday -
25°C, Saturday - 26°C, Sunday - 22°C. Find the average temperature, variance, and
standard deviation.
EXAMPLE:
Variance Standard Deviation
= 7
= 23°C

7. A dataset of temperature in degree Celsius (°C) was recorded for a period of seven
days: Monday - 22°C, Tuesday - 24°C, Wednesday - 21°C, Thursday - 21°C, Friday -
25°C, Saturday - 26°C, Sunday - 22°C
EXAMPLE:
TEMPERATURE (°C)
22 23 -1 1
24 23 1 1
21 23 -2 4
21 23 -2 4
25 23 2 4
26 23 3 9
22 23 -1 1
24

8. A dataset of temperature in degree Celsius (°C) was recorded for a period of seven
days: Monday - 22°C, Tuesday - 24°C, Wednesday - 21°C, Thursday - 21°C, Friday -
25°C, Saturday - 26°C, Sunday - 22°C
EXAMPLE:
= 24 / (7-1)
= 4
= 4
= 2 °C
Variance Standard Deviation

9. GROUPED DATA

10. STANDARD DEVIATION
VARIANCE
FORMULA
N
N
N
N

11. A dataset of temperature in degree Celsius (°C) was recorded for a period of a month.
Find the average temperature, variance, and standard deviation.
EXAMPLE:
CLASS (°C) FREQUENCY (f)
20-21 3
22-23 6
24-25 8
26-27 9
28-29 4

12. A dataset of temperature in degree Celsius (°C) was recorded for a period of a month.
Find the average temperature in a year, variance, and standard deviation.
EXAMPLE:
CLASS (°C) FREQUENCY (f) MIDPOINT (m) f (m)
20-21 3 20.5 61.5
22-23 6 22.5 135
24-25 8 24.5 196
26-27 9 26.5 238.5
28-29 4 28.5 114
∑ f 30 ∑ fm 745
= ∑ fm / ∑ f
= 745 / 30
= 24.83

13. A dataset of temperature in degree Celsius (°C) was recorded for a period of a month.
Find the average temperature in a year, variance, and standard deviation.
EXAMPLE:
CLASS (°C) FREQUENCY (f) MIDPOINT (m)
20-21 3 20.5 24.83 -4.33 18.7489 56.2467
22-23 6 22.5 24.83 -2.33 5.4289 32.5734
24-25 8 24.5 24.83 -0.33 0.1089 0.8712
26-27 9 26.5 24.83 1.67 2.7889 25.1001
28-29 4 28.5 24.83 3.67 13.4689 53.8756
∑ f 30 168.667
n = ∑ f
= 30

14. A dataset of temperature in degree Celsius (°C) was recorded for a period of a month.
Find the average temperature in a year, variance, and standard deviation.
EXAMPLE:
Variance Standard Deviation
= 168.667 / (30-1)
= 5.82
= 5.82
= 2.41 °C