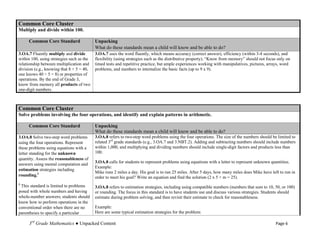
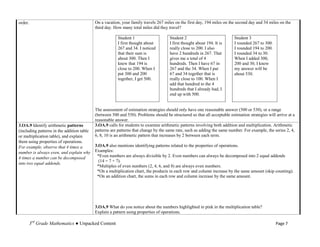
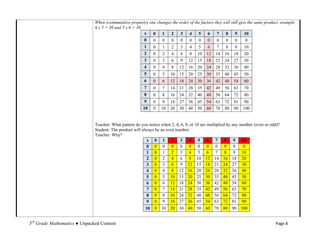
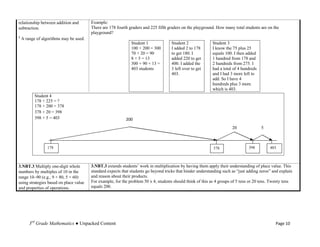
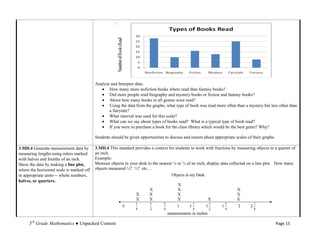
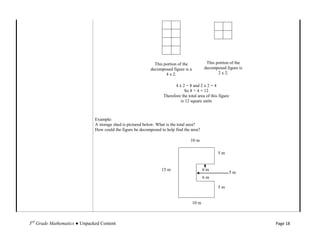
The document details the unpacked content for 3rd-grade mathematics aligned with the new Common Core State Standards for North Carolina, focusing on operations and algebraic thinking. It aims to assist educators in understanding what students must know and be able to do, offering descriptions and examples of each standard. The document encourages feedback to improve its utility for teachers.