The document outlines the syllabus for first-order logic at SRM Institute of Science and Technology, covering various concepts such as proofs, axiomatic systems, and inference rules. It details definitions, exercises, and examples related to first-order calculus and logical deductions. The content is structured to provide a comprehensive view of the principles of computational logic, including laws, consistency, and completeness of logical systems.

1. SRM
INSTITUTE OF SCIENCE ANDTECHNOLOGY,
Delhi-NCR Campus
COMPUTATIONAL LOGIC
UNIT4(FIRST ORDER LOGIC)
Mr. Naresh Sharma
Assistant Professor
Department of CSE
SRMIST/NCR

2. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
SYLLABUS
(PROOFS IN PREDICATE LOGIC)
• Axiomatic System FC
• Introduction
• Examples
• Theorems
• Monotonicity Deduction,
• RA,
• Fitness,
• Paradox of material
Implication,
• Strong Generalization
• Adequacy of FC to FL
• Compactness of FL
• Laws of FL
• Natural Deduction
• Analytic Tableaux

3. AXIOMATIC SYSTEM

4. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
TERMINOLOGIES
Finite sequence of formulas
Proof
Axiom
Derived by application of some inference rule on earlier formu
Theorem ⊢ X X is provable
Σ ⊢ Y
Last formula of proof ⊢FCX.
A set of formulas Σ is said to be inconsistent if there exists a formula Y such that Σ
⊢ Y and Σ ⊢ ¬Y , else Σ is said to be consistent.
Proof of the consequence
Consequence is provable
Proof System First order Calculus (FC)
Sequence of formulas

5. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
AXIOM SCHEMES OF FC
• (A1) X → (Y → X)
• (A2) (X → (Y → Z)) → ((X → Y ) → (X → Z))
• (A3) (¬X → ¬Y ) → ((¬X → Y ) → X)
• (A4) ∀xY → Y [x/t], provided x is free for t in Y.
• (A5) ∀x(Y → Z) → (Y → ∀xZ), provided x does not occur free in Y.
• (A6) (t ≈ t)
• (A7) ((s ≈ t) → (X[x/s] → X[x/t]), provided x is free for s, t in X.
Let X, Y, Z, be Formulas x be variable and s, t be terms
Axiom schemes of PC
Equality predicate
Semantic counterpart of ⊨∀X → X[x/t].
Quantifiers

6. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
DEFINITIONS AND RULES
(D1) p ∧ q ≐ ¬(p → ¬q)
(D2) p ∨ q ≐ ¬p → q
(D3) p ↔ q ≐ ¬((p → q) → ¬(q → p))
(D4) ⊤ ≐ p → p
(D5) ⊥ ≐ ¬(p → p)
(D6) ∃xX ≐ ¬∀x¬X
Single formula
Two formulas
Inference
Provided x is not free in any premise used thus far.

7. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
EXERCISES
• ∀x∀yX ⊢ ∀y∀xX
• ⊢ ∀xX → ∀xX – different from the one we discussed
• If x does not occur free in X, then ⊢ X → ∀xX.
• ∀x¬X ⊢ ¬∀xX
• ⊢ (s ≈ t) ⊢ (t ≈ s).

8. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
∀x∀yX ⊢ ∀y∀xX
⊢ ∀xX → ∀xX

9. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
If x does not occur free in X, then ⊢ X → ∀xX
X → X P
∀x(X → X) UG
∀x(X → X) → (X → ∀xX) A5
X → ∀xX MP
∀x¬X ⊢ ¬∀xX
∀x¬X P
∀x¬X → ¬X A4
1. ¬X MP
∀xX → X A4
(∀xX → X) → (¬X → ¬∀xX) Th
¬X → ¬∀xX MP
¬∀xX 1, MP
⊢ (s ≈ t) ⊢ (t ≈ s)
(s ≈ t) P
(s ≈ t) → ((s ≈ s) → (t ≈ s) A7,X=(x ≈ s)
(s ≈ s) → (t ≈ s) MP
(s ≈ s) A6
(t ≈ s) MP

10. THEOREMS
First Order Logic

11. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
RAA
• Same as that in PC
Let Σ be a set of formulas and let X be a formula. Σ ⊨ X iff Σ ∪ {¬X} is
inconsistent. Σ ⊨ ¬X iff Σ ∪ {X} is inconsistent
If i is a model of Σ, then as Σ ⊨w, i(¬ w) =0. If i ⊭ Σ , then i ⊭ x for
some x∈ Σ; hence i ⊭ Σ ∪{¬w}
If i is not a model of Σ, then i ⊭ Σ ∪{¬w} Thus Σ ∪{¬w} is unsatisfiable.
Conversely Let Σ∪{¬w} be unsatisfiable and i ⊨ Σ , then i(¬w)=0,
hence i ⊨ w, Therefore Σ⊨w

12. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
MONOTONOCITY
• Same as that in PC
Let Σ, Γ be set of formulas and X a formula. Suppose that Σ ⊆ Γ If Σ ⊨ X, then
Γ ⊨ X.
If Σ ⊨ p and i ⊨ Γ, then i(x)=1 for every x ∈ Γ.
As Σ ⊆ Γ, i(y)=1 for every y ∈ Σ,
i ⊨ Σ.
Since Σ ⊨ p, i(p)=1.
Therefore Γ ⊨ p

13. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
DEDUCTION
Let us assume that there is a proof P
whose last formula is X → Y then let
us prove Σ ∪ {X} ⊢ Y.
Let Σ be a set of formulas, and let X, Y be formulas. Then, Σ ⊨ X → Y iff Σ ∪ {X}
⊨ Y
X → Y Σ ⊢X → Y
X P in Σ ∪ {X}
Y MP
Let us assume that there is a proof P
whose last formula is Σ ∪ {X} ⊢ Y then
let us prove X → Y
If P has I formula; then it is Y ➾
axiom, Premise in Σ or X itself
Y → (X → Y ) A1
Y Axiom / Premise
X → Y MP
⊢ X → X PC Theorem
If Σ ⊨ X, then Γ ⊨ X Monotonocity
Σ ⊢ X → X

14. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
PROOF CONTD…
• Induction hypothesis: If P has number of formulas to be less than n, then there is a
proof of Σ ⊢ X → Y. Suppose that Σ ∪ {X} ⊢ Y has a proof P1 of n formulas. Then the
nth formula is Y.
• Y can be axiom, Premise in Σ or X itself
• Derived from two earlier formulas using MP
• Derived from an earlier formula by UG
Covered in base case
Y → (X → Y ) A1
Y Axiom / Premise
X → Y MP
⊢ X → X PC Theorem
If Σ ⊨ X, then Γ ⊨ X Monotonocity
Σ ⊢ X → X

15. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
PROOF CONTD…
• Derived from two earlier formulas using MP
m steps to derive Z, k steps to derive Z  Y. At step n
using steps m and m+k apply MP to derive Y
P1: 1.
m. Z
m+k. (Z → Y ) MP
n. Y m, m+k,
MP

16. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
PROOF CONTD…
P5: 1. …
.
.
.
i. X  Z
.
.
.
i+j. X → (Z → Y )
i+j+1 (X → (Z → Y )) → ((X → Z) → (X → Y )) A2
i+j+2 (X → Z) → (X → Y ) MP
i+j+3 X → Y MP
P2 (i steps): Σ ⊢ X → Z, P3 (j steps): Σ ⊢ X → (Z → Y )

17. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
PROOF CONTD…
m steps to derive A. At step n using steps m and n-1
apply UG to derive ∀x A
As Y = ∀xA, P5 is a proof for Σ ⊢ X → Y.

18. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
EXAMPLE
• ⊢ ∀x(X → Y ) → (∀x¬Y → ∀x¬X) Deduction Theorem
{∀x(X → Y ), (∀x¬Y) } ⊢ ∀x¬X
∀x(X → Y ) P
∀x (X → Y ) →(X → Y ) A4
X → Y MP
(X → Y ) → (¬Y →¬X) Th
1. (¬Y →¬X) MP
∀x¬Y P
∀x¬Y → ¬Y A4
¬Y MP
¬X 1,MP
∀x¬X UG
Back

19. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
EXAMPLE
• ⊢ ∀x(X → Y ) → (¬∀x¬X → ¬∀x¬Y ).
{∀x(X → Y ), (∀x¬Y) } ⊢ ∀x¬X Deduction Theorem
∀x(X → Y ) ⊢ (∀x¬Y) → (∀x¬X) Contraposition
⊢ (∀x¬Y → ∀x¬X) → (¬∀x¬X → ¬∀x¬Y ) MP
∀x(X → Y ) ⊢ ¬∀x¬X → ¬∀x¬Y Deduction Theorem
⊢ ∀x(X → Y ) → (¬∀x¬X → ¬∀x¬Y )

20. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
EXERCISES (RAA & DEDUCTION)
• ⊢ ∀x(X → Y ) → (¬∀x¬X → ¬∀x¬Y )
• If x is not free in Y , then ⊢ ¬(∀xX → Y ) → ∀x¬(X → Y )
• ⊢ ∀x((x ≈ f(y)) → Qx) → Qf(y).
• {Pa, ∀x(Px → Qx), ∀x(Rx → ¬Qx), Rb} ⊢ ¬(a ≈ b).
• ∀x∀y(f(x, y) ≈ f(y, x)), ∀x∀y(f(x, y) ≈ y) ⊨ ¬∀x¬∀y(x ≈ y)

21. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
If x is not free in Y , then ⊢ ¬(∀xX → Y ) → ∀x¬(X → Y )
⊢ ¬(∀xX → Y ) → ∀x¬(X → Y )
iff ¬(∀xX → Y ) ⊢ ∀x¬(X → Y )
iff {¬(∀xX → Y ), ¬∀x¬(X → Y )} is inconsistent.
iff ¬∀x¬(X → Y ) ⊢ ∀xX → Y
iff ¬∀x¬(X → Y ), ∀xX ⊢ Y
iff {¬∀x¬(X → Y ), ∀xX, ¬Y } is inconsistent.
iff ∀xX, ¬Y ⊢ ∀x¬(X → Y ).
∀xX P
∀xX → X A4
X MP
X → (¬Y → ¬(X → Y )) Th
¬Y → ¬(X → Y ) MP
¬Y P
¬(X → Y ) MP
∀x¬(X → Y ) UG

22. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
⊢ ∀X(X → Y ) → (¬∀X¬X → ¬∀X¬Y )
⊢ ∀x(X → Y ) → (¬∀x¬X → ¬∀x¬Y )
Iff {∀x(X → Y ), (∀x¬Y) } ⊢ ∀x¬X by deduction theorem
Iff {∀x(X → Y ), ∀x¬X, ∀x¬Y } is inconsistent, by RAA
Iff ∀x(X → Y ),(∀x¬Y) ⊢ ∀x¬X, by RAA
Proof

23. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
⊢ ∀X((X ≈ F(Y)) → QX) → QF(Y).
∀x((x ≈ f(y)) → Qx) P
∀x((x ≈ f(y)) → Qx) → ((f(y) ≈ f(y)) → Qf(y)) A4,
(f(y) ≈ f(y)) → Qf(y) MP
f(y) ≈ f(y) A6
Qf(y) MP
∀x((x ≈ f(y)) → Qx) ⊢ Qf(y).
⊢ ∀x((x ≈ f(y)) → Qx) → Qf(y)

24. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
{Pa, ∀x(Px → Qx), ∀x(Rx → ¬Qx), Rb} ⊢ ¬(a ≈ b).
∀x(Px → Qx) P
∀x(Px → Qx) → (Pa → Qa) A4
Pa → Qa MP
Pa P
1. Qa MP
a ≈ b P
(a ≈ b) → (Qa → Qb) A7
Qa → Qb MP
2. Qb 1,MP
∀x(Rx → ¬Qx) P
∀x(Rx → ¬Qx) → (Rb → ¬Qb) A4
Rb → ¬Qb MP
Rb P
3. ¬Qb MP

25. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
∀x∀y(f(x, y) ≈ f(y, x)), ∀x∀y(f(x, y) ≈ y) ⊨ ¬∀x¬∀y(x ≈
y)
1. ∀x∀y(f(x, y) ≈ y) P
2. ∀x∀y(f(x, y) ≈ y) → ∀y∀x(f(y, x) ≈ x) Th
3. ∀y∀x(f(y, x) ≈ x) MP
4. f(x, y) ≈ y 1,A4,MP
5. f(y, x) ≈ x 3,A4,MP
6. ∀x∀y(f(x, y) ≈ f(y, x)) P
7. f(x, y) ≈ f(y, x) A4,MP
8. x ≈ y 4,5,7,A7,MP
9. ∀y(x ≈ y) UG
10. ∀x¬∀y(x ≈ y) P
11. ∀x¬∀y(x ≈ y) → ¬∀y(x ≈ y) A4
12. ¬∀y(x ≈ y) MP

26. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
⊢ ¬(∀xX → Y ) → ∀x¬(X → Y )
iff ¬(∀xX → Y ) ⊢ ∀x¬(X → Y )
iff {¬(∀xX → Y ), ¬∀x¬(X → Y )} is inconsistent.
iff ¬∀x¬(X → Y ) ⊢ ∀xX → Y
iff {¬∀x¬(X → Y ), ∀xX} ⊢ Y
iff {¬∀x¬(X → Y ), ∀xX, ¬Y } is inconsistent.
iff {∀xX, ¬Y } ⊢ ∀x¬(X → Y )
∀xX P
∀xX → X A4
X MP
X → (¬Y → ¬(X → Y))Th
¬Y P
(¬Y → ¬(X → Y)) MP
¬(X → Y) MP
∀x ¬(X → Y) UG
If x is not a free variable of Y ⊢ ¬(∀xX → Y ) → ∀x¬(X → Y )

27. LAWS IN FL
First order Logic

28. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
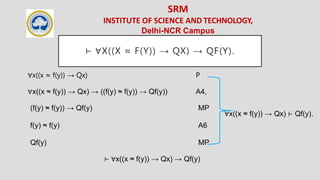
LAWS
Formulas X, Y, variables x, y, and terms r, s, t
• Constants: ∀x(⊥ → X) ≡ ⊤, ∃x(⊥ ∧ X) ≡ ⊥.
• Equality: (t ≈ t) ≡ ⊤, (s ≈ t) ≡ (t ≈ s), {r ≈ s, s ≈ t} ≡ (r ≈ t), {s ≈ t, X[x/s]} ≡ X[x/t].
• One-Point Rule: If x does not occur in t, then ∀x((x ≈ t) → X) ≡ X[x/t] and ∃x((x
≈ t) ∧ X) ≡ X[x/t].
• Empty Quantification: If x does not occur free in X, then ∀xX ≡ X and ∃xX ≡ X.
• De Morgan: ¬∀xX ≡ ∃x¬X, ¬∃xX ≡ ∀x¬X, ∀xX ≡ ¬∃x¬X, ∃xX ≡ ¬∀x¬X.
• Renaming: If x does not occur free in X, then ∀yX ≡ ∀x(X[y/x]) and ∃yX ≡
∃x(X[y/x]).

29. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
LAWS
• Commutativity: ∀x∀yX ≡ ∀y∀xX, ∃x∃yX ≡ ∃y∃xX, ∃x∀yX _ ∀y∃xX.
• Distributivity: ∀x(X ∧ Y ) ≡ ∀xX ∧ ∀xY, ∃x(X ∨ Y ) ≡ ∃xX ∨ ∃xY, ∀xX ∨ ∀xY
≡ ∀x(X ∨ Y ), ∃x(X ∧ Y ) ≡ ∃xX ∧ ∃xY.
• If x does not occur free in X, then
• ∀x(X ∨ Y ) ≡ X ∨ ∀xY, ∃x(X ∧ Y ) ≡ X ∧ ∃xY, ∀x(X → Y ) ≡ X → ∀xY,
• ∃x(X → Y ) ≡ X → ∃xY, ∀x(Y → X) ≡ ∃xY → X, ∃x(Y → X) ≡ ∀xY → X.

30. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
FOUR QUANTIfiER
LAWS
Let x be a variable free for a term t in a formula X. Let α be a parameter
not mentioned in Σ ∪ {X}
• Universal Specification (US): ∀xX ⊢ X[x/t].
• Existential Generalization (EG): X[x/t] ⊢ ∃xX.
• Universal Generalization (UG) : If Σ ⊢ X[x/α], then Σ ⊢ ∀xX.
• Existential Specification (ES): If Σ ∪ {X[x/α]} ⊢ Y , then Σ ∪ {∃xX} ⊢ Y.

31. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
∀X∀Y(F(X, Y) ≈ F(Y, X)), ∀X∀Y(F(X, Y) ≈
Y), ∀X¬∀Y(X ≈ Y) ⊨ ¬∀Y(X ≈ Y)
1. ∀x∀y(f(x, y) ≈ y) P
2. ∀x∀y(f(x, y) ≈ y) → ∀y∀x(f(y, x) ≈ x) Th
3. ∀y∀x(f(y, x) ≈ x) MP
4. f(x, y) ≈ y 1,A4,MP
5. f(y, x) ≈ x 3,A4,MP
6. ∀x∀y(f(x, y) ≈ f(y, x)) P
7. f(x, y) ≈ f(y, x) A4,MP
8. x ≈ y 4,5,7,A7,MP
9. ∀y(x ≈ y) UG
10. ∀x¬∀y(x ≈ y) P
11. ∀x¬∀y(x ≈ y) → ¬∀y(x ≈ y) A4
12. ¬∀y(x ≈ y) MP

32. NATURAL DEDUCTION

33. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
INFERENCE RULES
where c is a new constant not occurring in Y .
where y is a
new variable

34. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
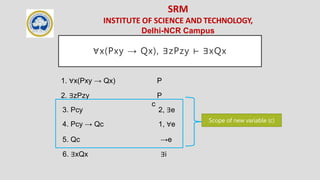
{∀x(Pxy → Qx), ∀zPzy} ⊢ ∀xQx
1. ∀x(Pxy → Qx) P
2. ∀zPzy P
3. Puy → Qu ∀e, [x/u]
4. Puy 2, ∀e
6. ∀xQx ∀i
u
5. Qu →e
Scope of new variable (u)

35. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
∀x(Pxy → Qx), ∃zPzy ⊢ ∃xQx
1. ∀x(Pxy → Qx) P
2. ∃zPzy P
3. Pcy 2, ∃e
4. Pcy → Qc 1, ∀e
5. Qc →e
6. ∃xQx ∃i
Scope of new variable (c)
c

36. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
EXERCISES
1. ⊢ ∀xX → X[x/t] for any term t free for x in X.
2. ⊢ ∀ x(X → Y ) → (X → ∀ xY ) if x is not free in X.
3. ⊢ (s ≈ t) → (X[x/s] → X[x/t]).
4. Pa, ∀x(Px → Qx), ∀x(Rx → ¬Qx), Rb |= ¬(a ≈ b).
5. ∀x(Lx → Fx) ⊢ ∀x(∃y(Ly ∧ Sxy) → ∃y(Fy ∧ Sxy))

37. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
1. ⊢ ∀xX → X[x/t] for any term t free for x in X
X[x/t] ∀e
∀xX CP
∀xX → X[x/t] →i

38. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
2. ⊢ ∀ x(X → Y ) → (X → ∀ xY ) if x is not free in X.
1. ∀x(X → Y ) CP
X CP
y
X → Y [x/y] 1, ∀e
Y [x/y] → e
∀xY ∀ i
X → ∀xY →i
∀x(X → Y ) → (X → ∀xY) →i

39. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
3. ⊢ (s ≈ t) → (X[x/s] → X[x/t]).
(s ≈ t) CP
X[x/s] CP
X[x/t] ≈e
X[x/s] → X[x/t] →i
(s ≈ t) → (X[x/s] → X[x/t]) →i

40. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
4. Pa, ∀x(Px → Qx), ∀x(Rx → ¬Qx), Rb ⊨ ¬(a ≈ b)
3. Pa P
1. ∀x(Px → Qx) P
6. ∀x(Rx → ¬Qx) P
5. Rb P
2. Pa → Qa ∀e
4. Qa →e
7. Rb → ¬Qb) ∀e
8. ¬Qb 5,7 → e
9. a ≈ b CP(assume)
10. ¬Qa 8,9, ≈
11. ⊥ 4,10
12. ¬ (a ≈ b) ¬i

41. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
5. ∀x(Lx → Fx) ⊢ ∀x(∃y(Ly ∧ Sxy) → ∃y(Fy ∧ Sxy))
1. ∀x(Lx → Fx) P
2. ∃y(Ly ∧ Sxy) CP
3. Lc ∧ Sxc c
4. Lc ∧e
5. Lc → Fc 1, ∀e
6. Fc →e
7. Sxc 3, ∧e
8. Fc ∧ Sxc ∧i
9. ∃y(Fy ∧ Sxy)) ∃i
10. ∃y(Fy ∧ Sxy)) ∃e
11. ∃y(Ly ∧ Sxy) → ∃y(Fy ∧ Sxy)) → i

42. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
∀x(Lx → Fx) ⊢ ∀x(∃y(Ly ∧ Sxy) → ∃y(Fy ∧ Sxy))

43. ANALYTIC TABLEAUX

44. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
PROPOSITIONAL TABLEAU
• Tree whose root is the proposition P and generated by
applying PT-rules.
• Children of a node is the denominator of the
corresponding rule
• Path: From root to a leaf
• Complete Path : Rule applied on every compound
proposition
• Closed Path: Contains ⊥ or p and ¬p for some atomic or
constant proposition
• Open Path: Path which is not closed
Stacking rules
Branching rules
Completed
Closed tableau Open tableau

45. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
EXAMPLE
• (p ∨ q )∧( q ∨ r)
1. p ∨ q
2. q ∨ r
3. p q
4. q r q r

46. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
SHOW {P→(¬Q→R),P→¬Q,¬(P→R)}
INCONSISTENT
1. p→(¬q→r)
2. p→¬q
3. ¬(p→r)
4. p
5. ¬r
6. ¬p 7. ¬q
8. ¬p. 9. ¬q→r. 10. ¬p. 11. ¬q→r
12. ¬¬q 13. r 14. ¬¬q 15. r
16. q 17. q
x
x
x
x
x
x
Closed Tableau hence Inconsistent

47. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
SHOW {P→(¬Q→R),P→¬Q,¬(P→R)}
INCONSISTENT
1. p→(¬q→r)
2. p→¬q
3. ¬(p→r)
4. p
5. ¬r
6. ¬p 7. ¬q
8. ¬p 9. ¬q→r
10. ¬¬q 11. r
12. q
x
x
x
x

48. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
ADDITIONAL RULES OF INFERENCE
• The restriction of ‘t is a new term’ means that if s
is a sub-term of t, then s neither occurs in
• The current formula,
• Nor in any premise used so far in the path,
• Nor in any formula introduced to the path by an
existential rule.
• Apply all stacking rules before applying any
branching rule whenever possible
• Apply existential rules before applying universal
rules.
t is a constant that has not occurred earlier in the path.
Use the (∃) and (¬∀) rules before applying the

49. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
⊢ ∀xX → X[x/t]
where x is free for term t in X.
¬(∀xX → X[x/t])
1. ∀xX
¬X[x/t]
X[x/t] 1, (∀)
¬ (¬∀xX ∨ 𝑋[x/t]) ) (∀xX ∧ ¬𝑋[x/t]) )
∀xX
X

50. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
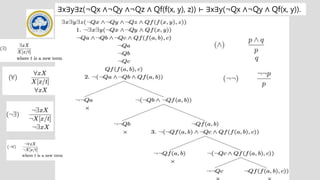
⊢ ∀x(X → Y ) → (X → ∀xY )
where x is not free in X
¬(∀x(X → Y ) → (X → ∀xY )
1. ∀x(X → Y )
¬(X → ∀xY )
X
¬∀xY
¬Y [x/c ] new constant c
X → Y [x/c] 1, x not free in X
¬X Y [x/c]
X → Y = ¬X ∨ Y

51. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
∃x∃y∃z(¬Qx ∧¬Qy ∧¬Qz ∧ Qf(f(x, y), z)) ⊢ ∃x∃y(¬Qx ∧¬Qy ∧ Qf(x, y)).

52. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
EXERCISES
• ⊢ (t ≈ t)
• ⊢ (s ≈ t) → (X[x/s] → X[x/t]), where x is free for terms s, t in X.
• ⊢ ∃x(∃yPy → Px)
• {∃xPx, ¬Pc}.
• {∃xPx ∧ ∃xQx, ¬∃x(Px ∧ Qx), ∀xPx → Ps}.
• {∀x(Px → Qx), ∃xPx, ∀x¬Qx, ∃xPx ∨ ¬Pc}.
• ∀x(∃y(Pxy ∧ Qy) → ∃z(Rz ∧ Pxz)) ⊨ ¬∃xRx → ∀x∀y(Pxy → ¬Qy).
• {∀x∃yPxy, ∀x∀y∀z((Pxy ∧ Pyz) → Pxz), ¬∃xPxx}.

53. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
SOLUTIONS
⊢ (t ≈ t)
¬(t ≈ t)
(t ≈ t) (≈ )
X

54. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus

55. SRM
INSTITUTE OF SCIENCE AND TECHNOLOGY,
Delhi-NCR Campus
ADDITIONAL EXERCISES
• {∃xPx, ¬Pc}.
• {∃xPx ∧ ∃xQx, ¬∃x(Px ∧ Qx), ∀xPx → Ps}.
• {∀x(Px → Qx), ∃xPx, ∀x¬Qx, ∃xPx ∨ ¬Pc}.
• ∀x(∃y(Pxy ∧ Qy) → ∃z(Rz ∧ Pxz)) _ ¬∃xRx → ∀x∀y(Pxy →
¬Qy).
• {∀x∃yPxy, ∀x∀y∀z((Pxy ∧ Pyz) → Pxz), ¬∃xPxx}.