- Logic is the study of principles of reasoning and determining valid inferences. Propositional logic deals with propositions that can be either true or false.
- A propositional calculus defines rules for combining propositions using logical operators like conjunction, disjunction, negation, implication, and biconditional.
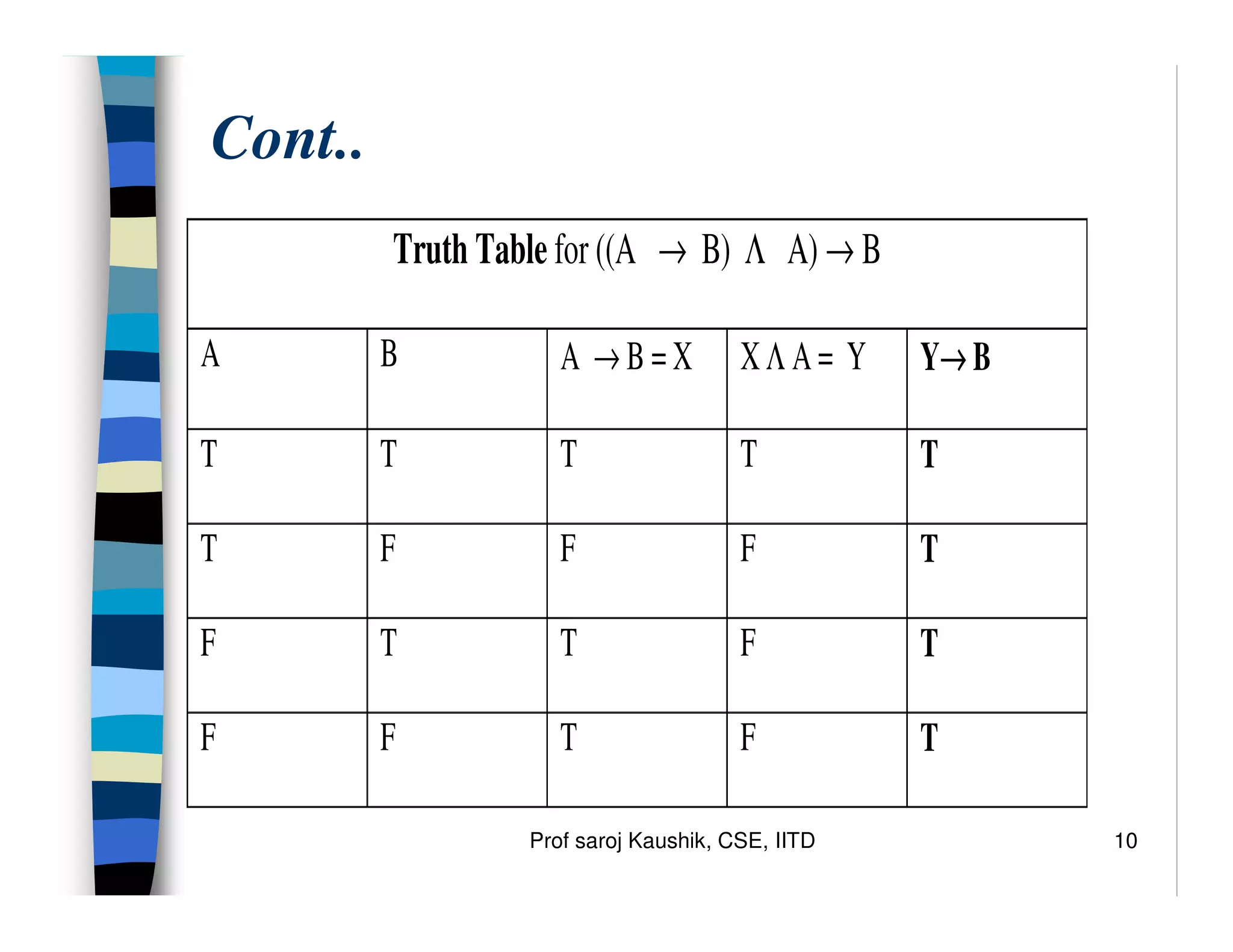
- Truth tables define the meanings of logical operators by listing their truth values under all combinations of true and false propositions.
- Natural deduction is a system to derive logical consequences through inference rules like introduction and elimination rules for logical operators. It mimics natural patterns of reasoning.