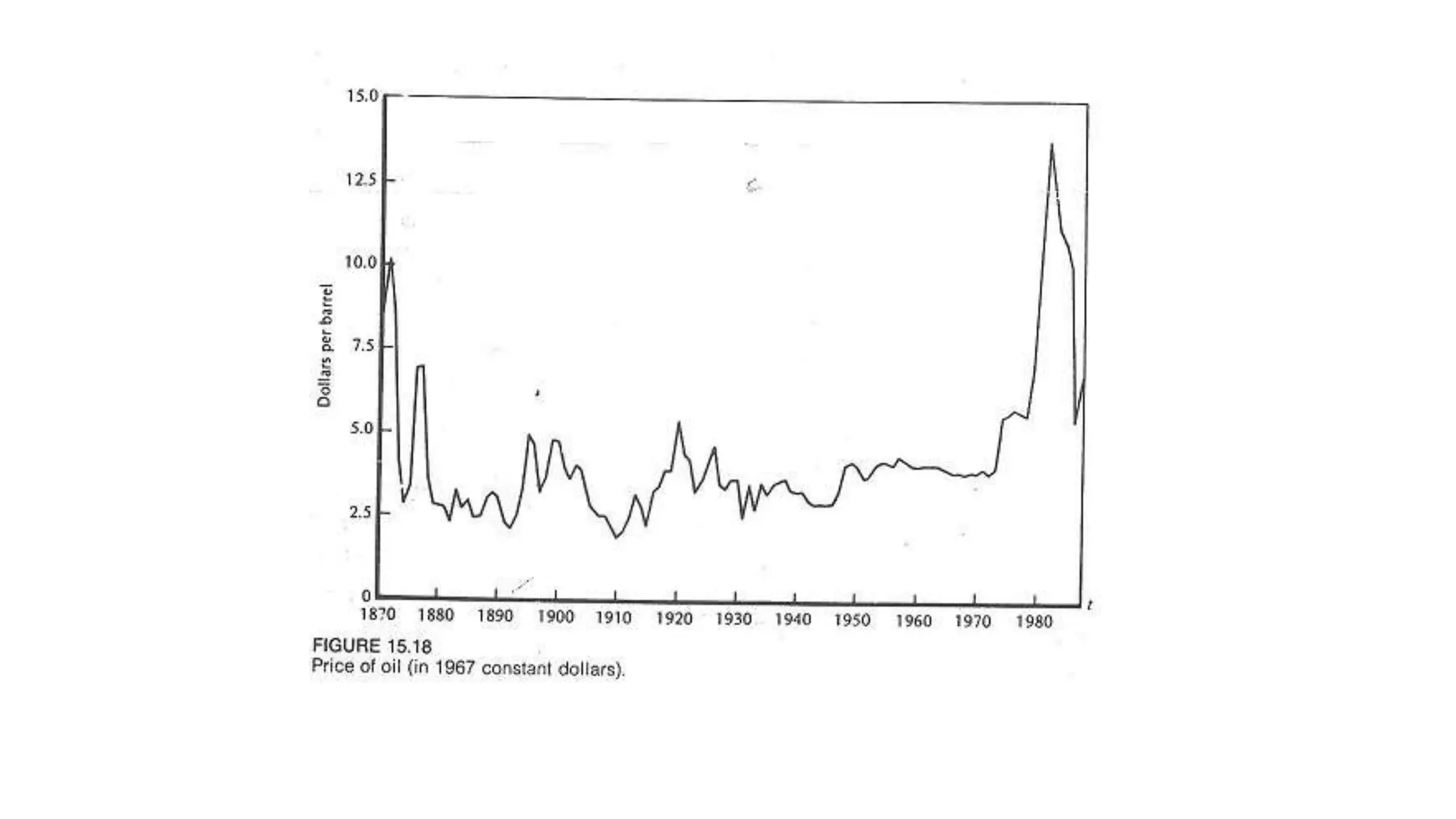
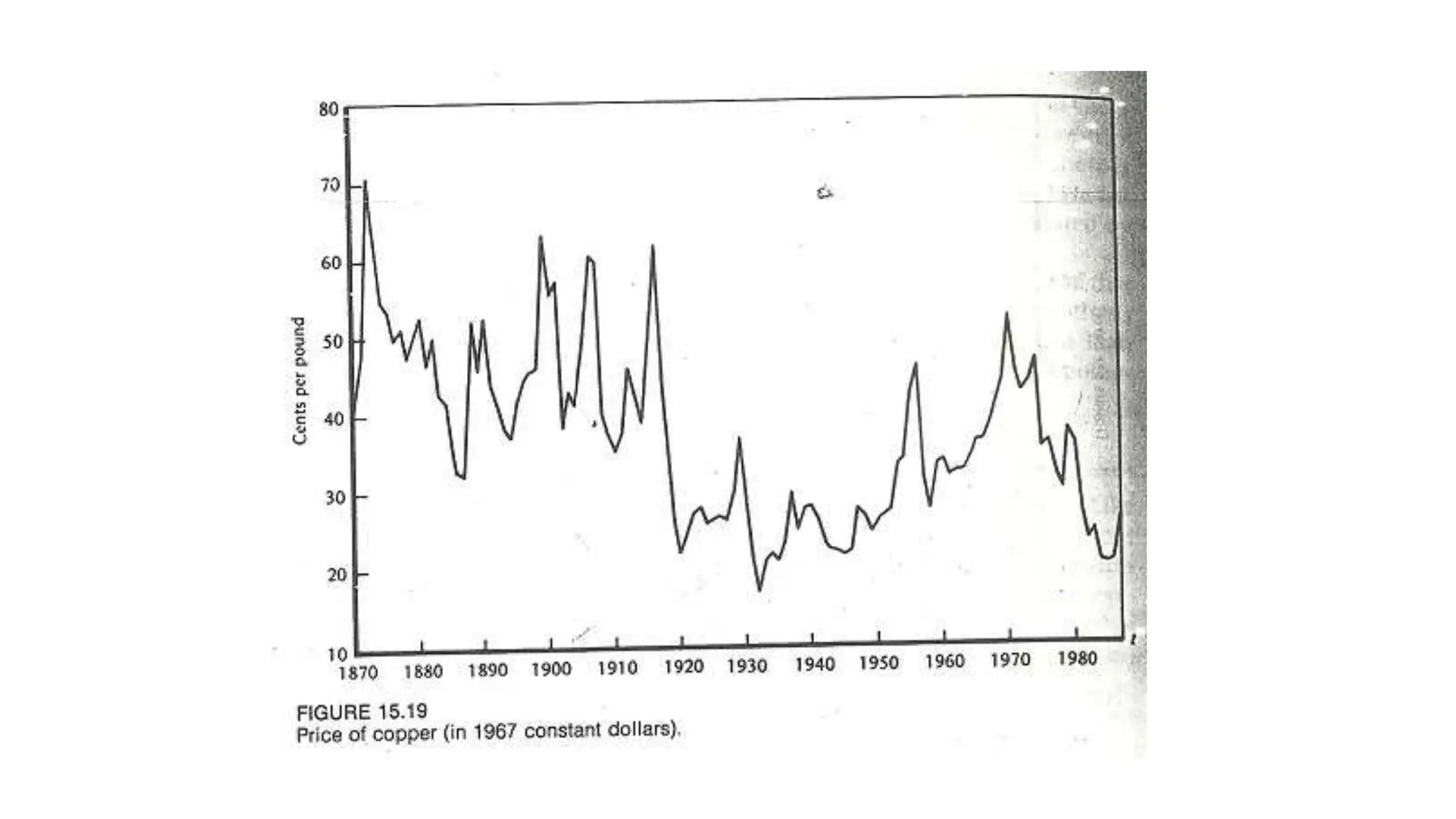
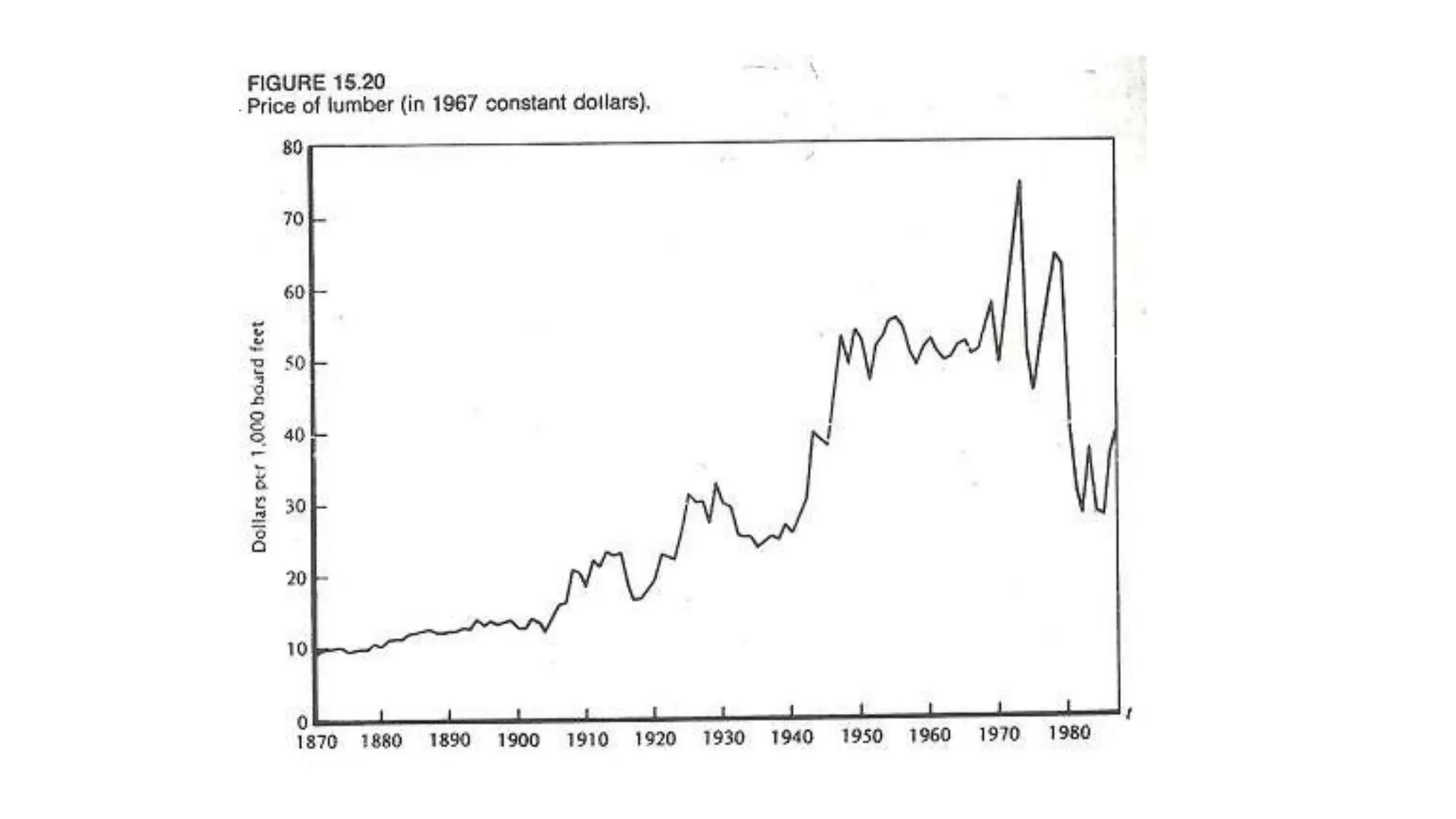
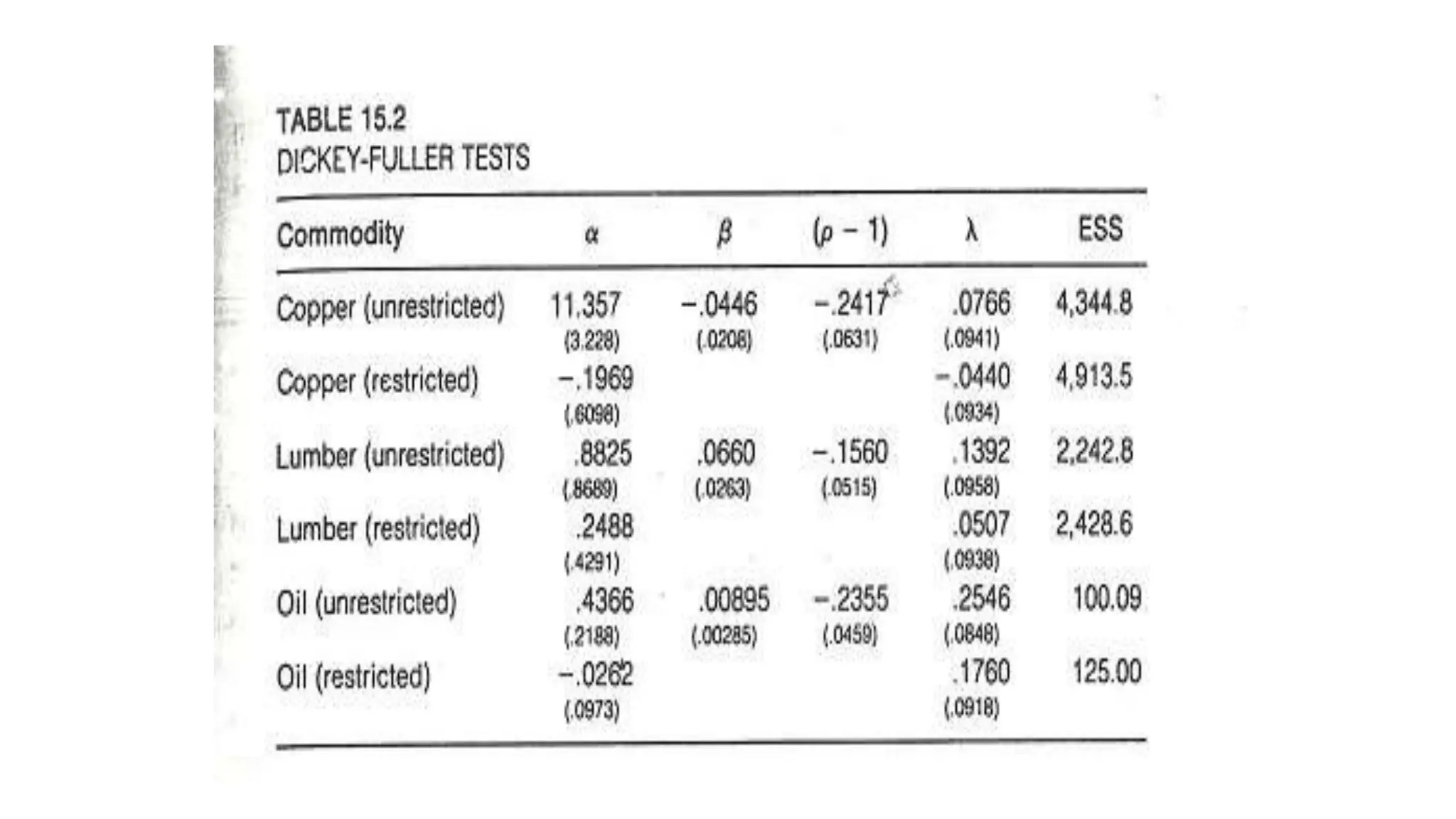
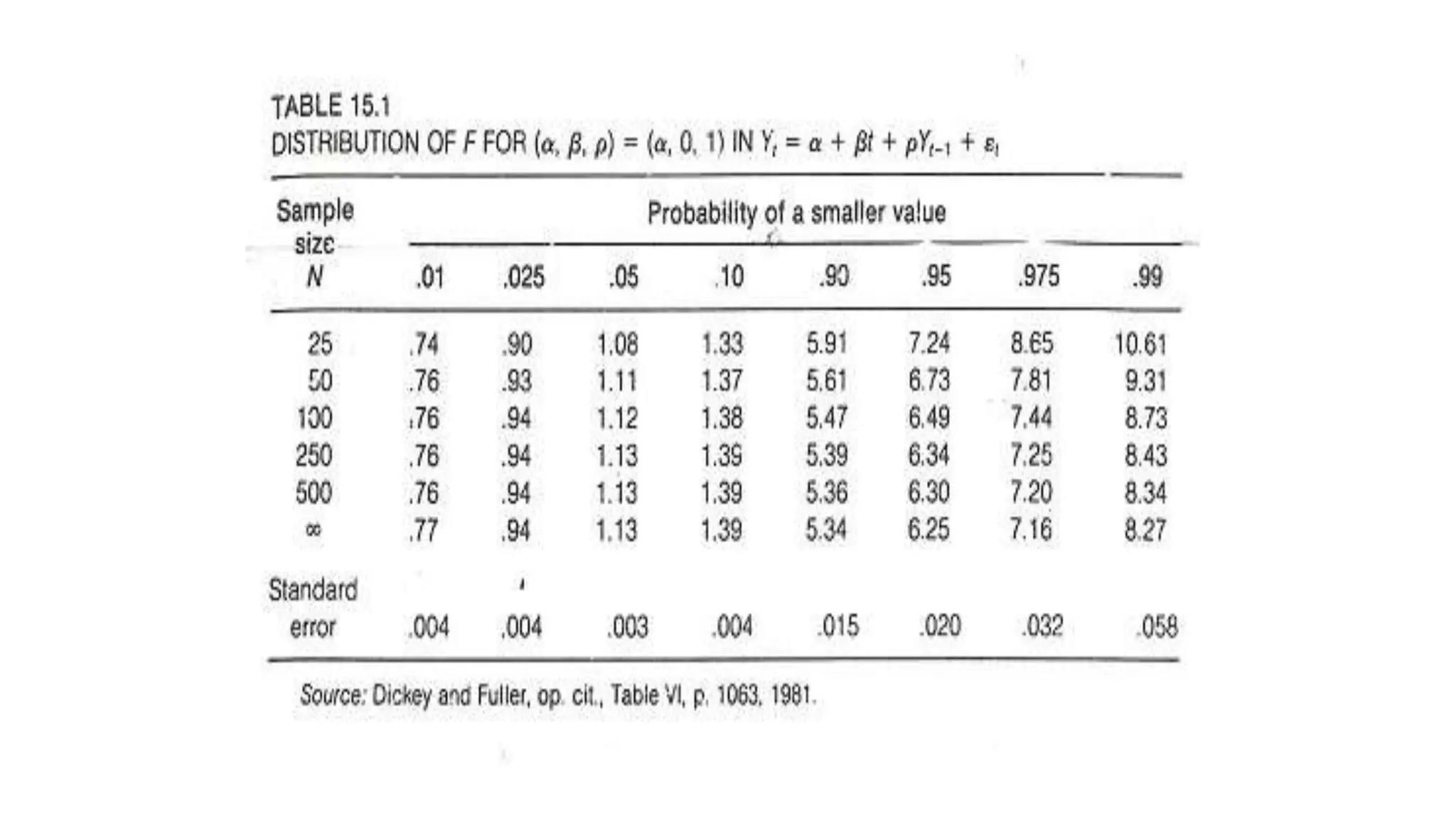
The document discusses unit root tests, which are used to determine whether a time series follows a random walk or stationary process. If a series has a unit root and follows a random walk, it has implications for regression analysis and economic forecasting. Common unit root tests introduced by Dickey, Fuller, and others test the null hypothesis that a time series has a unit root by examining the t-statistic on the coefficient of the lagged dependent variable. Standard OLS tests are invalid for unit root testing, so alternative test methods were developed.

1. Unit Root and Unit Root
Tests
Pindyck and Rubinfeld, Chap 15

2. Testing for Random Walks
• Qus: Do economic variables like GDP, employment and interest rates
tend to revert back to some long-run trend after experiencing a shock
or do they follow random walks?

3. • This question is important for two reasons:
1. If they follow RW, a regression of one against another can lead to
spurious results.
• Remember, a RW does not have finite variance, so the Gauss Markov
theorem will not hold and OLS will not yield a consistent parameter
estimator.
• Detrending the variables before running the regression will not help—
the detrended series will still be non-stationary.
• Only first (higher order) differencing will yield a stationary series.
• Detrending: Run—
the residuals from this—
provide the de-trended series.

4. 2. The answer has implications for our understanding of the economy
and forecasting.
• If a variable like GDP follows a RW, the effects of a temporary shock
(oil price increase) will not dissipate after some years—it will become
permanent.
• Because only the lagged value that matters is the immediate one in
RW
and that too in its entire magnitude.

5. • In a study on macro time series, Nelson and Plosser found evidence
that GDP and other time series behave like RWs.
• Many studies followed and found that many economic time series do
appear to be RW or at least have RW components.
• Most of these studies use what are called “Unit Root Tests.”
• Introduced by David Dickey and Wayne Fuller. DF Test
• Philip Perron Test (PP), KPSS Test (Kwiatkowski, Phillips, Schmidt,
and Shin

6. Unit Root Tests
• Suppose we believe that a variable , which has been
growing over time, can be described by the following:
• One possibility is that has been growing because it has a
positive trend, .
• Would become stationary after detrending. Implies only a fraction of
lagged value has an effect on . .
• Another possibility is that has been growing because it follows
a RW with a positive drift (i.e., )
• In this case we would want to work with . (Differenced Series)
• Detrending would not make this series stationary.

7. • Can we estimate this equation using OLS and use the t-statistic on
to test whether is significantly different from one?
• If true value of is indeed one, then the variance is not finite and
the standard OLS tests of significance are invalid.
• In particular, the OLS estimate of is biased towards zero.
• Incorrectly reject the null hypo of RW.
• This problem led to the development of a series of alternative tests to
determine whether = 1; These are called “Unit Root Tests.”

19. Augmented Dickey Fuller Test