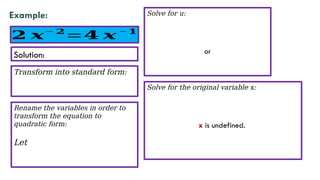
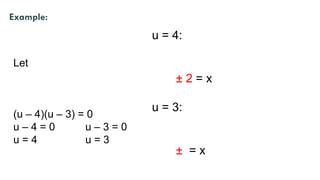The document outlines the process of transforming various equations into quadratic forms to solve them effectively. It details steps for solving equations, including renaming variables, checking for extraneous roots, and examples of rational equations. Additionally, it provides examples of expressing quadratic equations in standard form and finding their solutions.

1. TRANSFORMING EQUATIONS INTO
QUADRATIC FORMS

2. Objective:
Solve equations transformable to quadratic equations (including rational
algebraic equations).
Solve problems involving quadratic equations and rational algebraic
equations

3. Steps in Solving Equations Transformable to Quadratic Forms
1. Transform the equation to general form.
2. Rename the variables in order to transform the equation to quadratic form.
3. Apply the most appropriate technique to solve the resulting quadratic
equation.
4. Check the extraneous roots. (Extraneous – an apparent root that does not
solve the given equation).

4. How to solve rational equations?
A rational equation is an equation that involves one or more rational
expressions.
The following are examples of rational equations.
1
4
+
1
5
=
1
𝑡
1
3
−
5
6
=
1
𝑥
𝑥 −8
3
+
𝑥 −3
2
=0
In solving rational equations, it is always important to check if the number are true solutions
Extraneous Solutions – some values which when substituted to the rational equation do not
satisfy the conditions because of the restrictions in the denominator of the equation.

5. Example: Express the following quadratic equation in standard form. Write the
equation with a positive coefficient for the 2nd
degree term. Solve.
𝟏𝟎
𝒙
+𝟏=𝟑 𝒙
𝒙 (𝟏𝟎
𝒙
+𝟏)=(𝟑 𝒙 )𝒙
𝟏𝟎+ 𝒙=𝟑 𝒙𝟐
𝟑 𝒙𝟐
− 𝒙 − 𝟏𝟎=𝟎
(𝟑 𝒙+𝟓) (𝒙 −𝟐)=𝟎
(𝟑 𝒙+𝟓)=𝟎 𝒐𝒓 ( 𝒙 − 𝟐)=𝟎
𝒙=−
𝟓
𝟑
𝒙=𝟐
The solutions are:

6. 𝟒
𝒙
+
𝟒
𝒙+𝟔
=𝟏
Example: Express the following quadratic equation in standard form. Write the
equation with a positive coefficient for the 2nd
degree term. Solve.
(𝒙)(𝒙+𝟔)(𝟒
𝒙
+
𝟒
𝒙 +𝟔)=𝟏( 𝒙)(𝒙 +𝟔)
𝟒(𝒙 +𝟔)+𝟒 (𝒙 )=𝒙𝟐
+𝟔 𝒙
𝟒 𝒙+𝟐𝟒+𝟒 𝒙=𝒙𝟐
+𝟔 𝒙
𝟖 𝒙+𝟐𝟒=𝒙𝟐
+𝟔 𝒙
𝒙𝟐
+𝟔𝒙 −𝟖 𝒙−𝟐𝟒=𝟎
𝒙𝟐
−𝟐 𝒙−𝟐𝟒=𝟎
( 𝒙 +𝟒)( 𝒙 − 𝟔)=𝟎
𝒙 +𝟒=𝟎 𝒙=−𝟒
𝒙 −𝟔=𝟎𝒙=𝟔
The solutions are:

7. Divide all the terms by 3.
3 (2x + 7) (x – 3) = 0
2x + 7 = 0 x – 3 = 0
2x = -7 x =
3
Example: Express the following quadratic equation in standard form. Write the
equation with a positive coefficient for the 2nd
degree term. Solve.
The solutions are:

8. (8y +3)(y – 1) = 0
8y + 3 = 0 y – 1 =
0
8y = -3 y = 1
y = -3/8
Example: Express the following quadratic equation in standard form. Write the
equation with a positive coefficient for the 2nd
degree term. Solve.
The solutions are:

9. Example:
𝟐 𝒙− 𝟐
=𝟒 𝒙 −𝟏
Transform into standard form:
Solution:
Rename the variables in order to
transform the equation to
quadratic form:
Let
Solve for u:
or
Solve for the original variable x:
x is undefined.

10. Check:
𝟐 𝒙− 𝟐
=𝟒 𝒙 −𝟏
Solve for the original variable x:
The only solution is

11. Let
(u – 4)(u – 3) = 0
u – 4 = 0 u – 3 = 0
u = 4 u = 3
Example:
u = 4:
± 2 = x
u = 3:
± = x

12. Let
(u – 3)(u + 2) = 0
u – 3 = 0 u + 2 = 0
u = 3 u = -2
Example:
u = 3:
± = x
u = -2:
0 = x

13. Activity:
Solve the following equations.

14. 𝟔
𝒙
+𝟐=𝟒 𝒙
Example: Express the following quadratic equation in standard form. Write the
equation with a positive coefficient for the 2nd
degree term. Solve.

15. Example: Express the following quadratic equation in standard form. Write the
equation with a positive coefficient for the 2nd
degree term. Solve.
(𝟕−𝟐 𝒙 )𝒙=𝟔

16. Example: Express the following quadratic equation in standard form. Write the
equation with a positive coefficient for the 2nd
degree term. Solve.
√𝟕 𝒙
𝟐
+𝟓 𝒙−𝟑=𝒙

17. 𝟔
𝒙
+𝟐=𝟒 𝒙
Example: Express the following quadratic equation in standard form. Write the
equation with a positive coefficient for the 2nd
degree term. Solve.

18. 𝟔
𝒙
+𝟐=𝟒 𝒙
Example: Express the following quadratic equation in standard form. Write the
equation with a positive coefficient for the 2nd
degree term. Solve.