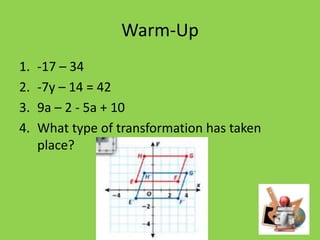
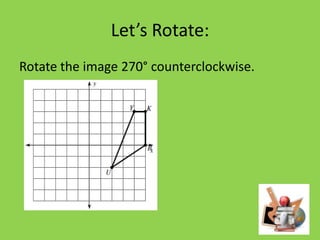
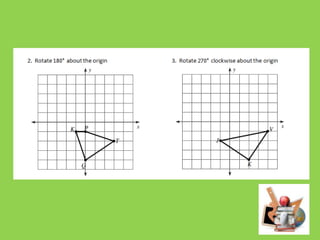
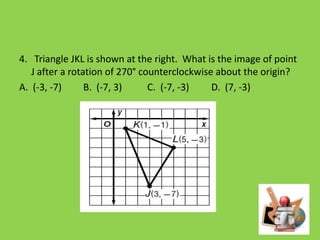
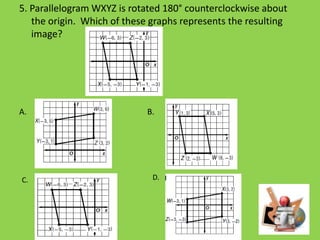
This document discusses transformations such as rotations, reflections, and translations. It provides examples of rotating figures 270 degrees counterclockwise, where the x-coordinate becomes the y-coordinate and the y-coordinate becomes the negative of the x-coordinate. Students are given problems to graph rotated images and identify the results of rotating figures by specific degrees around the origin.

1. Warm-Up
1.
2.
3.
4.
-17 – 34
-7y – 14 = 42
9a – 2 - 5a + 10
What type of transformation has taken
place?

2. Essential Question
What transformations have we learned about?
Give a mini-example of each.

3. Rotations Day 2
Unit 1, Day 8

4. Common Core GPS
MCC8.G.1: Verify experimentally the properties of
rotations, reflections, and translations:
a. Lines are taken to lines, and line segments to line segments
of the same length.
b. Angles are taken to angles of the same measure.
c. Parallel lines are taken to parallel lines.
MCC8. G. 2: Understand that a two-dimensional figure is
congruent to another if the second can be obtained from
the first by a sequence of rotations, reflections, and
translations; given two congruent figures, describe a
sequence that exhibits the congruence between them.

5. Language of the Standards
What is a…
Rotation?
Angle of rotation?

6. Rotating
To rotate an image 270° counterclockwise about
the origin:
(x, y) becomes (y, -x).
What rule
does this
look like??

7. Let’s Rotate:
Rotate the image 270° counterclockwise.

8. Work Session:
Graph the image using the given transformation.

10. 4. Triangle JKL is shown at the right. What is the image of point
J after a rotation of 270° counterclockwise about the origin?
A. (-3, -7)
B. (-7, 3)
C. (-7, -3)
D. (7, -3)

11. 5. Parallelogram WXYZ is rotated 180° counterclockwise about
the origin. Which of these graphs represents the resulting
image?
A. B.
C.
B.
D.

12. Closing
What questions do you have about unit 1? Quiz
this Friday!