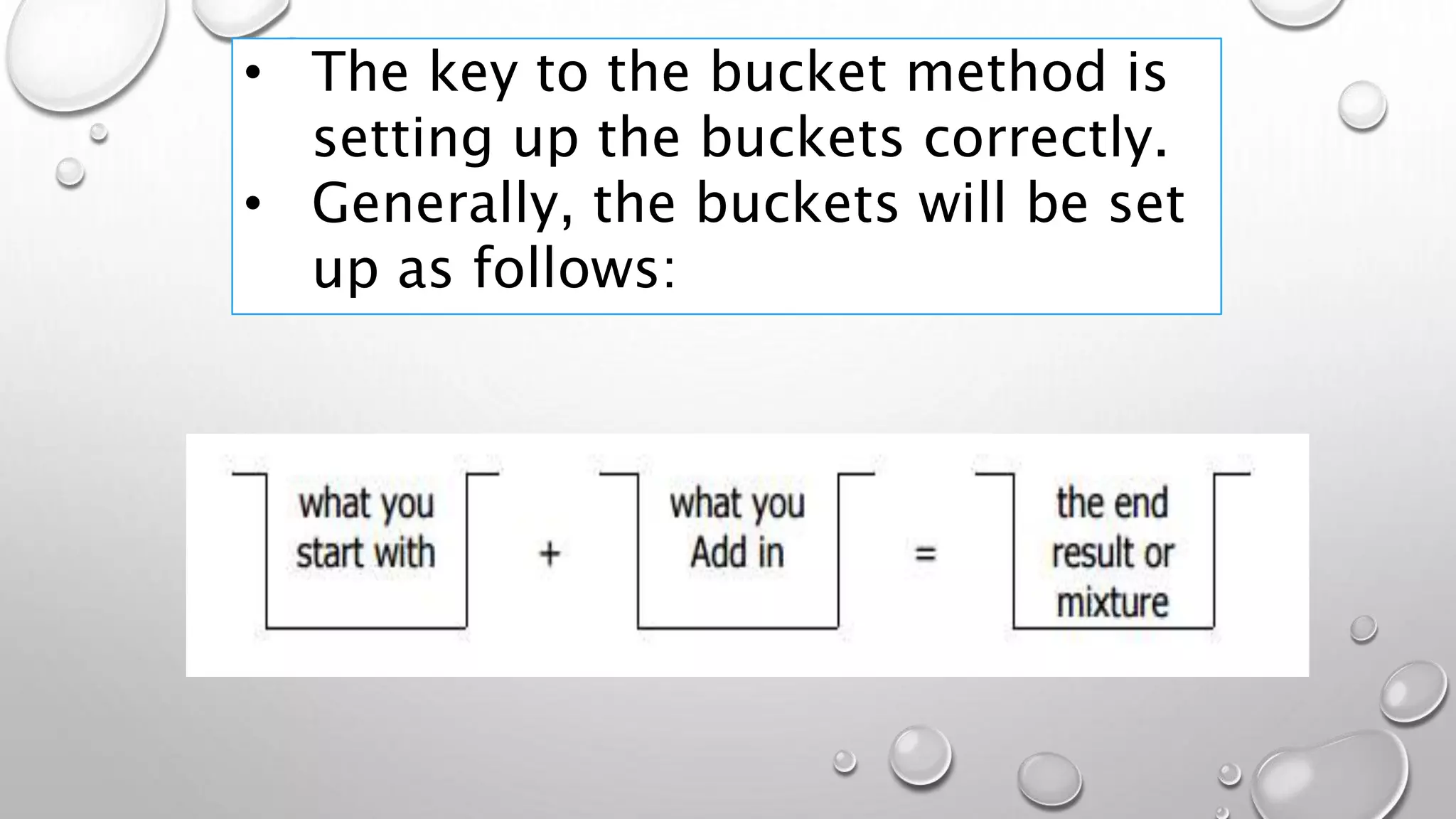
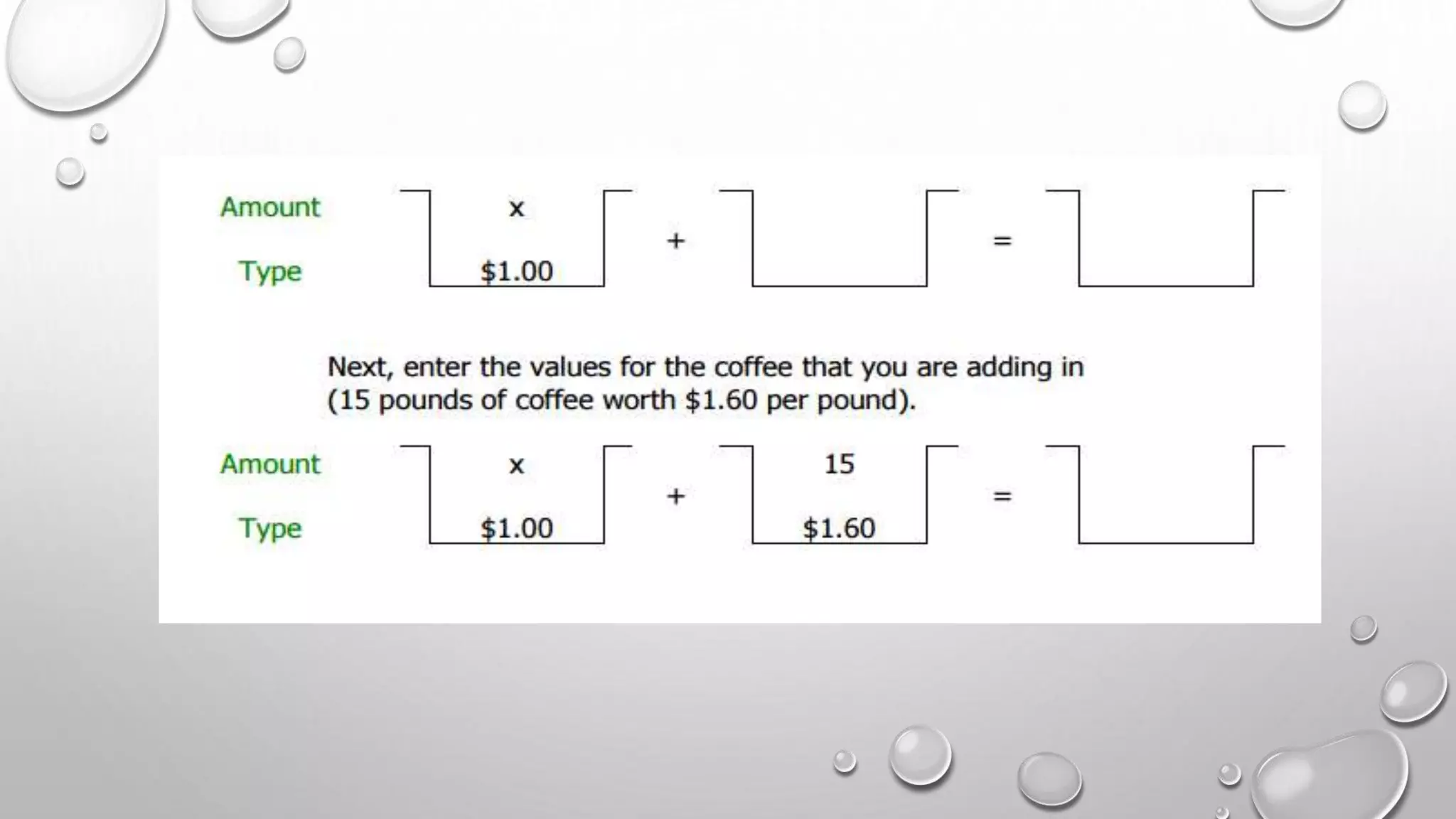
Mixture problems involve combining substances to create a new blend. This document provides examples of mixture problems from different contexts like business and chemistry. It then introduces the "bucket method" for systematically setting up and solving mixture problems. This involves defining amounts and properties of each initial substance as well as the desired final mixture, and setting up equations to relate these values. Several examples demonstrate setting up and solving equations to determine the amounts needed to create a final mixture with specified properties.

2. Mixture problems occur in many
different situations. For example, a
store owner may wish to combine
two goods in order to sell a new
blend at a given price. A chemist
may wish to obtain a solution of a
desired strength by combining other
solutions. In any case, mixture
problems may all be solved by using

3. • The key to the bucket method is
setting up the buckets correctly.
• Generally, the buckets will be set
up as follows:

4. • Each bucket must contain two
values: •
 An amount (liters, tons,
pounds, ounces, grams, etc.)
 A type (usually either a
percent or a price)

5. Example 1: How many pounds of
coffee worth $1.00 per pound must
be mixed with 15 pounds of coffee
worth $1.60 per pound to obtain a
blend worth $1.20 per pound?

8. •HOW MANY LITERS OF 20%
ALCOHOL SOLUTION SHOULD BE
ADDED TO 40 LITERS OF A 50%
ALCOHOL SOLUTION TO MAKE A
30% SOLUTION?

9. • LET X BE THE QUANTITY OF THE 20% ALCOHOL SOLUTION TO BE
ADDED TO THE 40 LITERS OF A 50% ALCOHOL. LET Y BE THE
QUANTITY OF THE FINAL 30% SOLUTION. HENCE
X + 40 = Y
• WE SHALL NOW EXPRESS MATHEMATICALLY THAT THE QUANTITY
OF ALCOHOL IN X LITERS PLUS THE QUANTITY OF ALCOHOL IN THE
40 LITERS IS EQUAL TO THE QUANTITY OF ALCOHOL IN Y LITERS.
BUT REMEMBER THE ALCOHOL IS MEASURED IN PERCENTAGE
TERM.
20% X + 50% * 40 = 30% Y

10. • SUBSTITUTE Y BY X + 40 IN THE LAST EQUATION TO OBTAIN.
20% X + 50% * 40 = 30% (X + 40)
• CHANGE PERCENTAGES INTO FRACTIONS.
20 X / 100 + 50 * 40 / 100= 30 X / 100 + 30 * 40 / 100
• MULTIPLY ALL TERMS BY 100 TO SIMPLIFY.
20 X + 50 * 40 = 30 X + 30 * 40

11. •STERLING SILVER IS 92.5% PURE
SILVER. HOW MANY GRAMS OF
STERLING SILVER MUST BE MIXED
TO A 90% SILVER ALLOY TO
OBTAIN A 500G OF A 91% SILVER
ALLOY?

12. •Let x and y be the weights, in grams, of sterling silver and
of the 90% alloy to make the 500 grams at 91%. Hence
x + y =500
•The number of grams of pure silver in x plus the number of
grams of pure silver in y is equal to the number of grams of
pure silver in the 500 grams. The pure silver is given in
percentage forms. Hence
92.5% x + 90% y = 91% 500

13. •Substitute y by 500 - x in the last
equation to write
92.5% x + 90% (500 - x) = 91% 500
•Simplify and solve
92.5 x + 45000 - 90 x = 45500
x = grams

14. • HOW MANY KILOGRAMS OF PURE
WATER IS TO BE ADDED TO 100
KILOGRAMS OF A 30% SALINE
SOLUTION TO MAKE IT A 10%
SALINE SOLUTION.

15. •Let x be the weights, in Kilograms, of pure water to
be added. Let y be the weight, in Kilograms, of the
10% solution. Hence
x + 100 = y
•Let us now express the fact that the amount of salt in
the pure water (which 0) plus the amount of salt in the
30% solution is equal to the amount of salt in the
final saline solution at 10%.
0 + 30% 100 = 10% y

16. •Substitute y by x + 100 in
the last equation and solve.
30% 100 = 10% (x + 100)
•Solve for x.
x = Kilograms

17. • A 50 ML AFTER-SHAVE LOTION
AT 30% ALCOHOL IS MIXED WITH
30 ML OF PURE WATER. WHAT IS
THE PERCENTAGE OF ALCOHOL
IN THE NEW SOLUTION?

18. •The amount of the final mixture is given by
50 ml + 30 ml = 80 ml
•The amount of alcohol is equal to the amount of alcohol in pure
water ( which is 0) plus the amount of alcohol in the 30%
solution. Let x be the percentage of alcohol in the final solution.
Hence
0 + 30% 50 ml = x (80)
•Solve for x x = 0.1817 = 18.75%