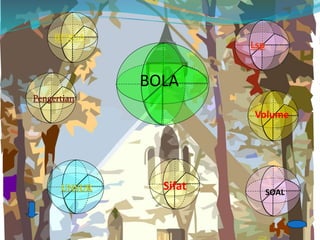
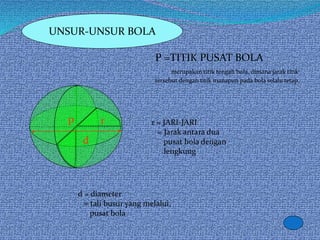
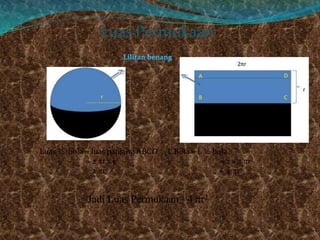
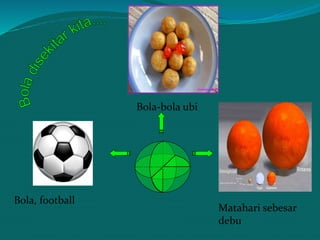
Dokumen ini membahas pengertian dan sifat-sifat bola, termasuk rumus volume dan luas permukaannya. Dikenal sebagai hasil karya Archimedes, rumus luas permukaan bola dinyatakan sebagai 4πr². Selain itu, terdapat contoh perhitungan volume bola dengan jari-jari 3 cm.

1. LINGKARAN

2. BENDA
Lsp
BOLA
SOAL
Pengertian
UNSUR Sifat
Volume

3. Bola adalah himpunan semua
titik-titik pada ruang yang berjarak
sama (jari-jari) terhadap titik
tertentu (disebut pusat).

4. UNSUR-UNSUR BOLA
r
d
P =TITIK PUSAT BOLA
merupakan titik tengah bola, dimana jarak titik
tersebut dengan titik manapun pada bola selalu tetap.
p
d = diameter
= tali busur yang melalui,
pusat bola
r = JARI-JARI
= Jarak antara dua
pusat bola dengan
lengkung

5. p r
d

6. Luas permukaan
• Pada tahun 287-212 M seorang matematikawan yang
bernama Archimedes telah menemukan rumus permukaan
bola. Hal ini tertuang dalam karyanya yang berjudul “On
Sphres And Cylinders“. Archimedes menyatakan dalil yakni
“Sebarang tabung yang alasnya kongruen dengan lingkaran
terbesar pada bola dan tingginya sama dengan diameter
bola, luas permukaan tabung itu sama dengan satu
setengah kali luas permukaan bola”.
• Penjelasan dalil itu merupakan bahwa perbandingan luas
permukaan bola dengan luas permukaan / sisi termasuk
sisi alas dan atas tabung terkecil yang muatannya adalah 2 :
3

7. Luas Permukaan
Luas ½ bola = luas panjang ABCD L Bola = L ½ bola
= 2 πr x r = 2 x 2 πr2
= 2 πr2 = 4 πr2
Jadi Luas Permukaan =4 πr2

8. Sebuah bola bekel dengan jari-jari 3 cm. Carilah Volume ?
• Jawab :
• Diketahui : r bola =3 cm
• Ditanyakan : Vol ?
• Penyelesaian : Vol Bola =
3
3
4
r
3
3..
3
4

36
=
=

9. Bola, football
Bola-bola ubi
Matahari sebesar
debu

10. TRIMAKASIH