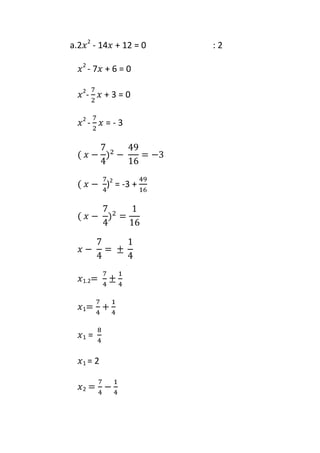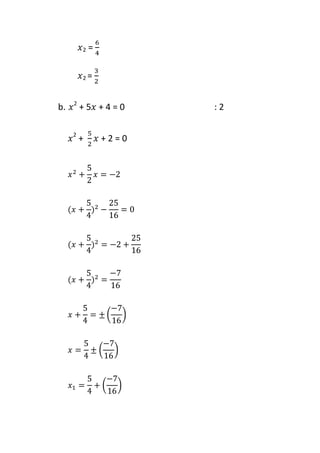This document contains information about a group assignment in Indonesian, including: 1. The name of the group leader and members. 2. Details of the assignment which involves factorizing quadratic equations, completing the square to put equations in the form x^2=p, and using the ABC formula. 3. Steps provided as examples to solve parts of the assignment involving factorizing, completing the square, and using the ABC formula.

1. KELOMPOK b
KETUA :
NI LUH GEDE WITASARI (02)
HP : 081999112677
ANGGOTA KELOMPOK :
1.I PUTU PRAMANA PUTRA (18)
2.NI WAYAN NITA ANGGRENI (21)
3.NI KADE INDAH PADMA YANI (31)
4.I GUSTI AYU PUTU DIAN PUTRI LESTARI (32)
TUGAS II
1. Cara Pemfaktoran.
a. x2 + 5x – 50 = 0
x2 + 10x – 5x – 50 = 0
x( x + 10 ) – 5 ( x + 10 ) = 0
( x – 5 ) ( x + 10 ) = 0
( x – 5) = 0 atau (x + 10) = 0
b. x2 + 3x = 0
x(x+3)=0
x = 0 atau (x + 3) = 0

2. c. x2 – 4 = 0
(x–2)(x+2)
Diuji = ( x – 2 ) ( x + 2 )
= x2 + 2x –2x – 4
= x2 – 4
(x – 2) = 0 atau (x + 2) = 0
d. 2x2 + 3x + 1 = 0
2x2 + 1x + 2x + 1 = 0
x ( 2x + 1 ) + 1 ( 2x + 1 ) = 0
( x + 1 ) ( 2x + 1 ) = 0
(x + 1) = 0 atau (2x + 1) = 0
e. 3x2 + 5x – 2 = 0
3x2 + 6x – 1x – 2 = 0
3x ( x + 2 ) – 1 ( x + 2 ) = 0
( 3x – 1 ) ( x + 2 ) = 0
(3x – 1) = 0 atau( x + 2) = 0
2. Dengan Melengkapkan Kuadrat Sempurna yaitu Diubah Menjadi
Bentuk x2 = p

3. 2
a.2
- 14 + 12 = 0
2
-7 +6=0
2
-
+3=0
2
-
=-3
)2 = -3 +
1.2
1
1
=
1=
2
2
:2

4. 2
=
2=
b.
2
+5 +4=0
2
+
+2=0
:2

5. 2
2
2
3.Menggunakan Rumus ABC.
a.
a = 1, b= -15, c= 30

6. b.
a = 1, b = 8, c = -20
1.2
1.2
-4
6

7. 1
1
-2
2
=-4 – 6
2
c.
-4 + 6
=-10
2
+3 =0
1.2
1.2
1.2
1.2
1.2
1
2
menjadi x2 + 3x + 0 =0
a = 1, b = 3, c = 0

8. 4. Menentukan p agar persamaan kuadrat (p + 3)x2 + 3x – 4 = 0 mempunyai dua
akar sama.