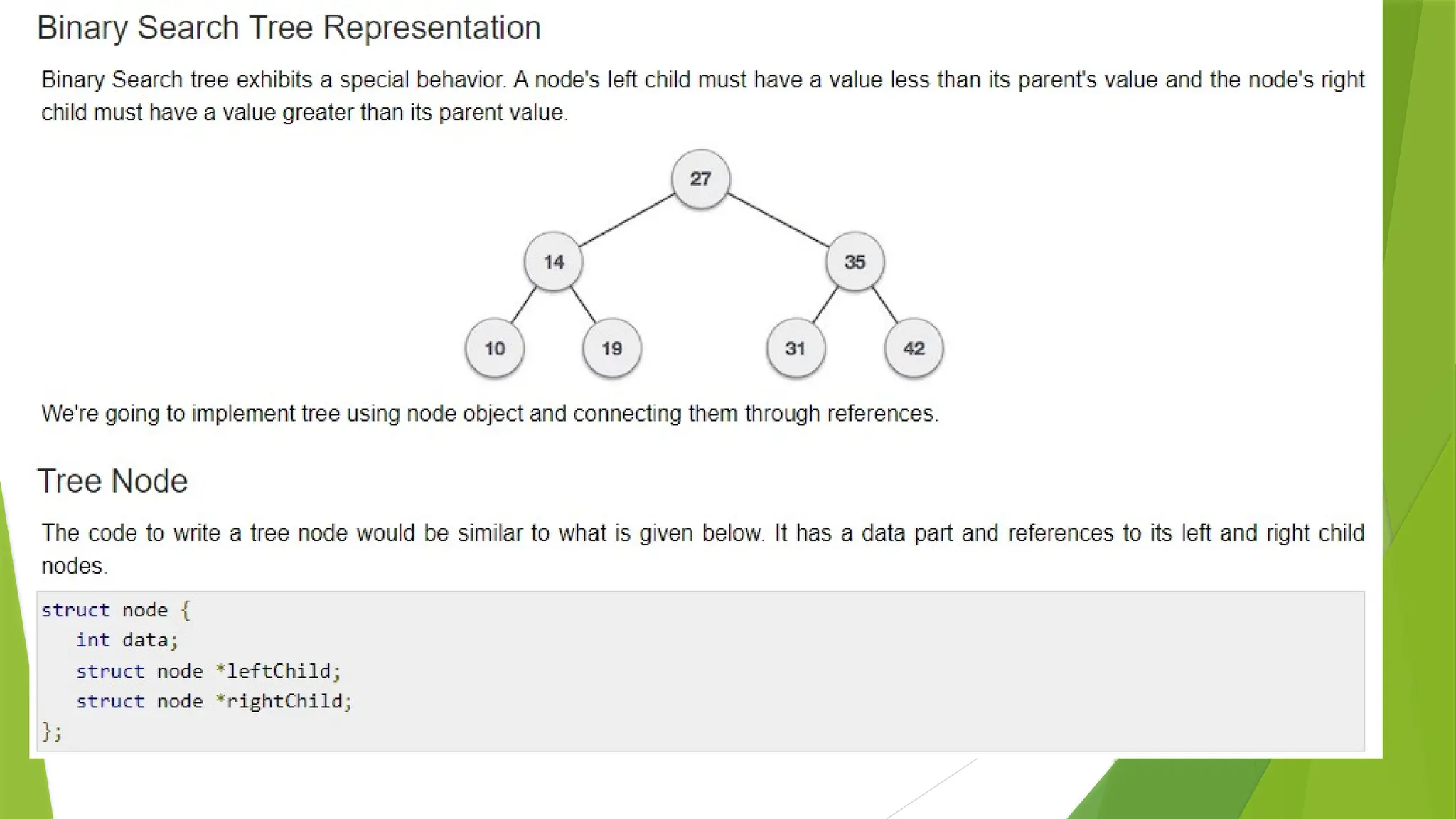
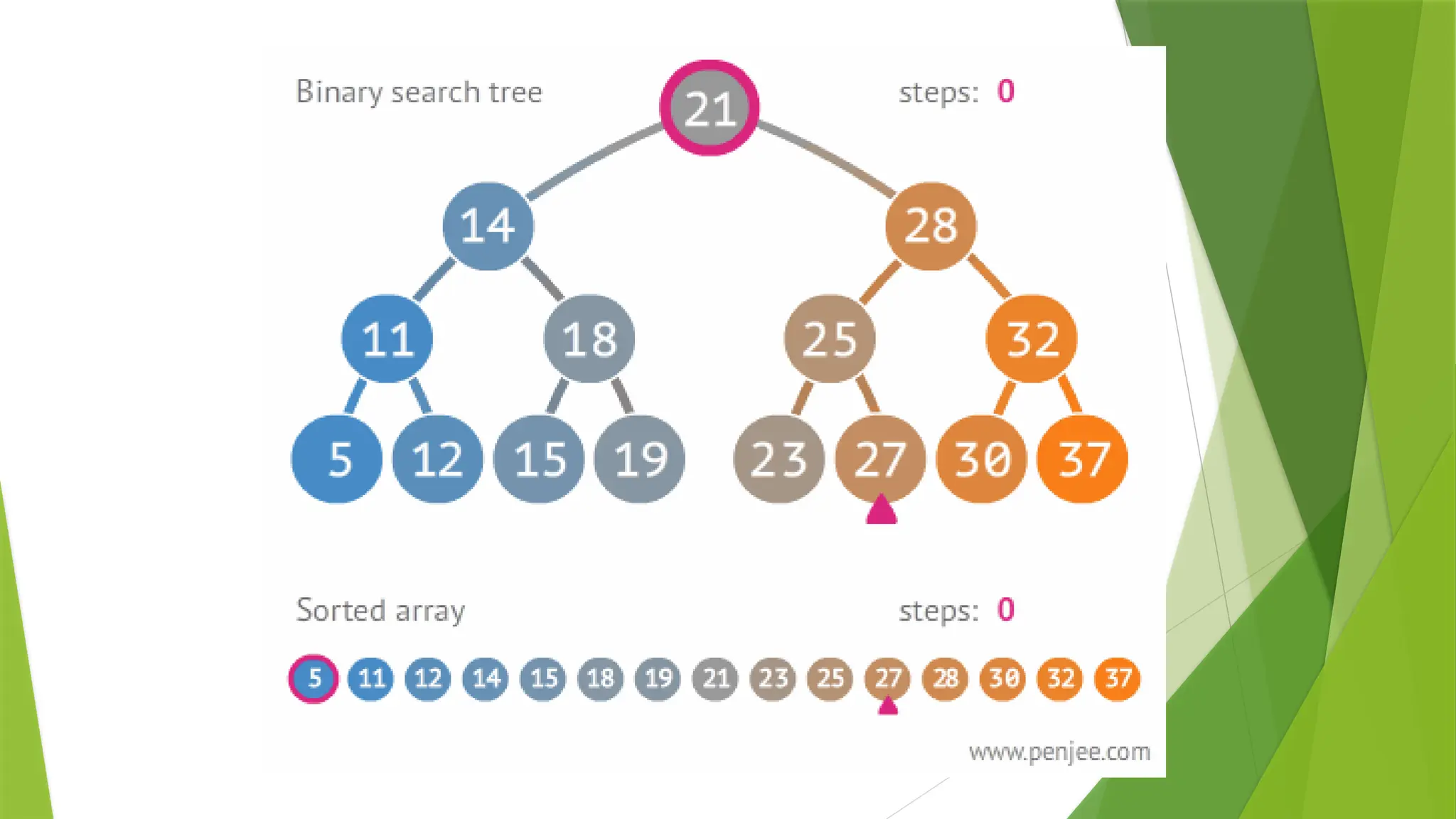
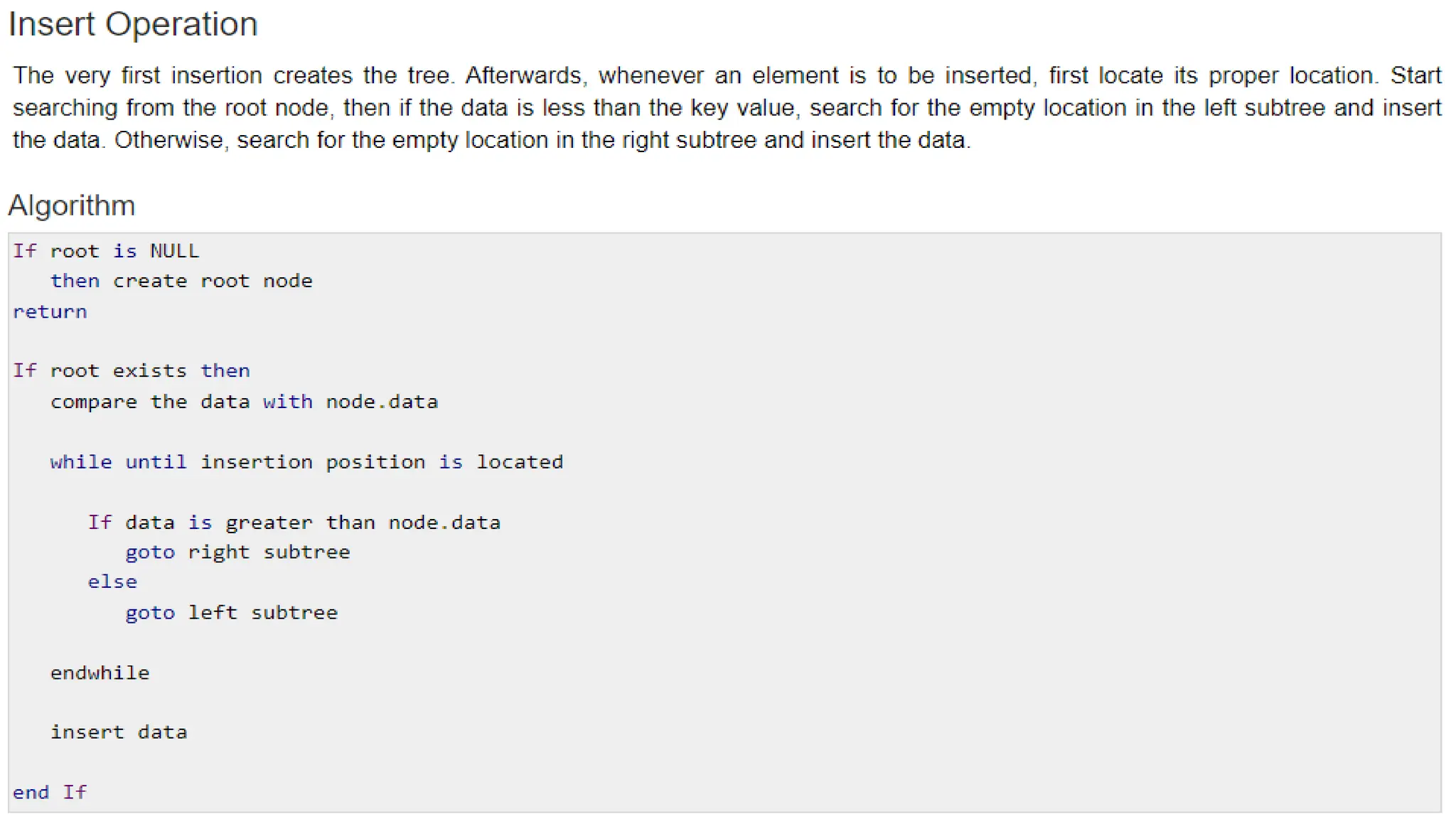
The document covers the concept of trees as a nonlinear data structure, detailing binary trees, their representation, and traversals. It discusses binary search trees (BST), their operations, including AVL trees, and practical applications like expression and decision trees. Additionally, it lists programming exercises related to BST functions, tree balance checks, and various tree metrics.

1. Trees
 Concept of nonlinear data structure
 Trees and binary trees-concept and terminology
 Sequential & Linked representation of binary trees
 Algorithm for tree traversals
 Binary search trees(BST)
 BST operations, AVL Trees
 Applications of binary tree : expression tree, decision tree

17. Left-Right Rotation
Double rotations are slightly complex
version of already explained versions of
rotations. To understand them better, we
should take note of each action performed
while rotation. Let's first check how to
perform Left-Right rotation. A left-right
rotation is a combination of left rotation
followed by right rotation.

19. Right-Left Rotation
The second type of double rotation
is Right-Left Rotation. It is a
combination of right rotation
followed by left rotation.

20. Practice Questions
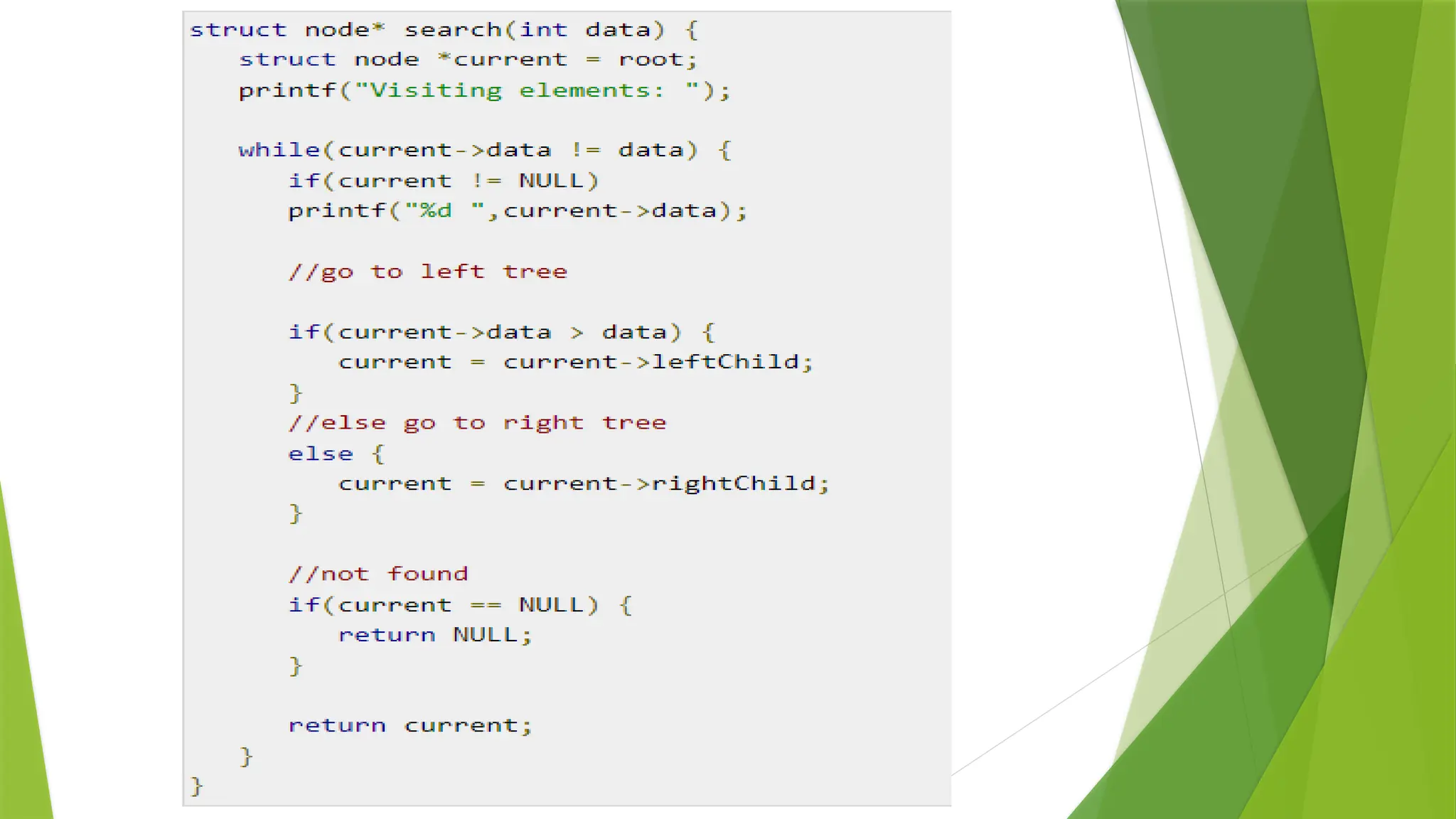
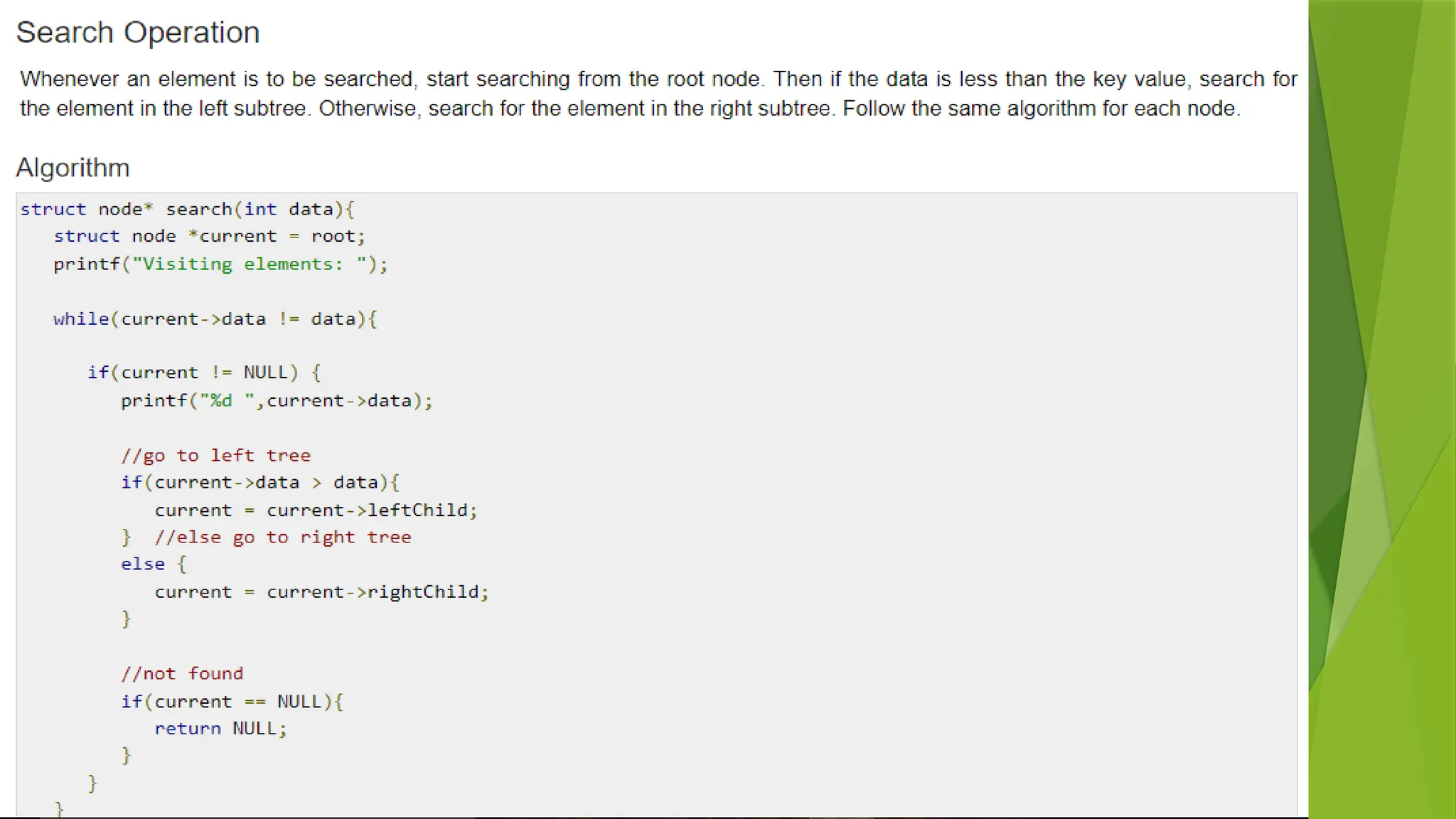
1. Implement functions for searching, deleting, and finding the minimum and maximum elements in a binary search
tree.
2. Write a program to find and print the minimum and maximum elements in a BST.
3. Write a program to count the number of nodes within a given range [low, high] in a BST.
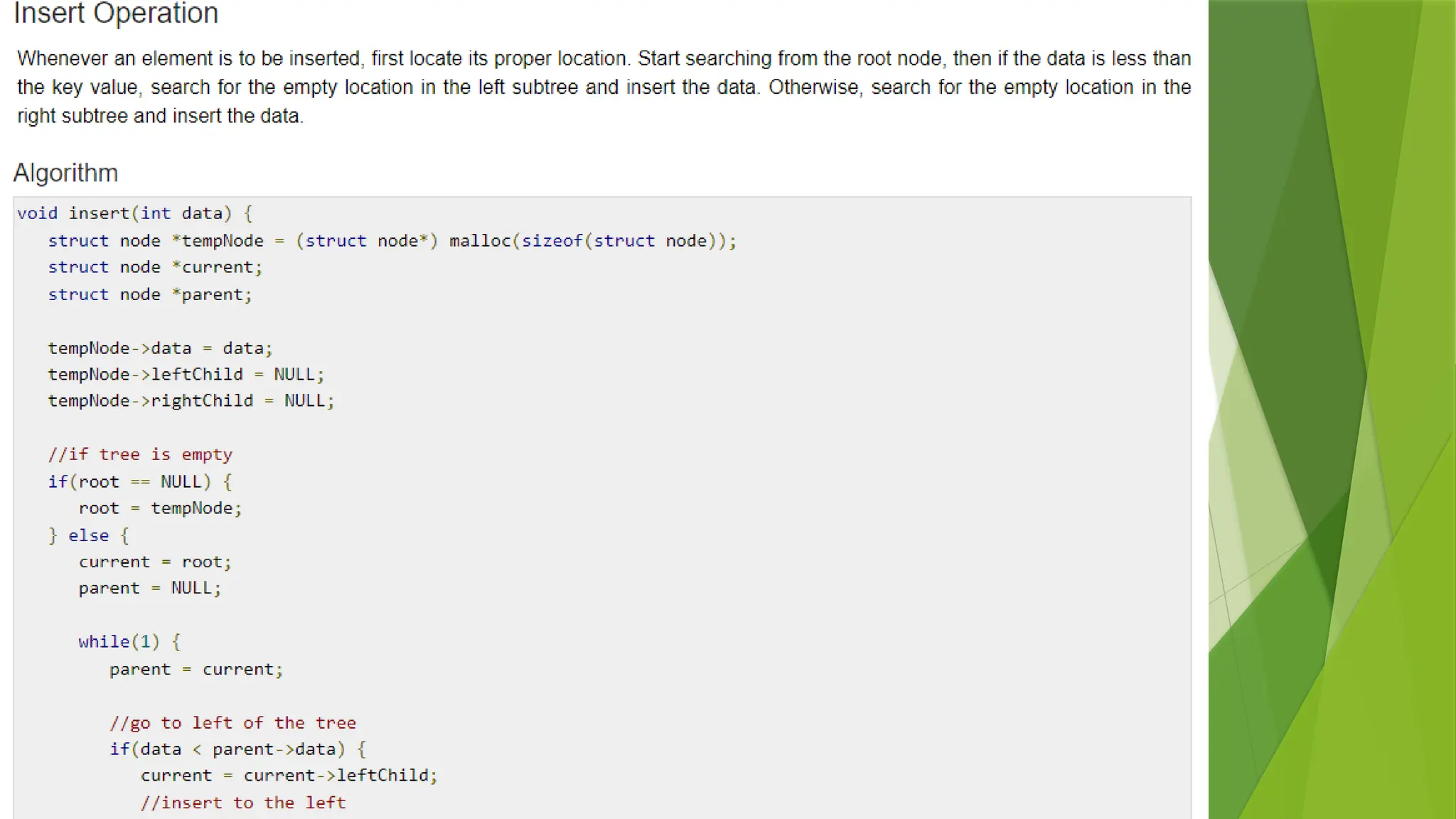
4. Create a program to use a BST for storing and searching real-world data, such as student records or inventory items.
Evaluate the system's efficiency for frequent insertions and deletions
5. Write a program to check whether a given binary tree is a BST.
6. Write a program to compute the sum of the depths of all nodes in a BST. Evaluate how this metric can provide
insights into tree balance.
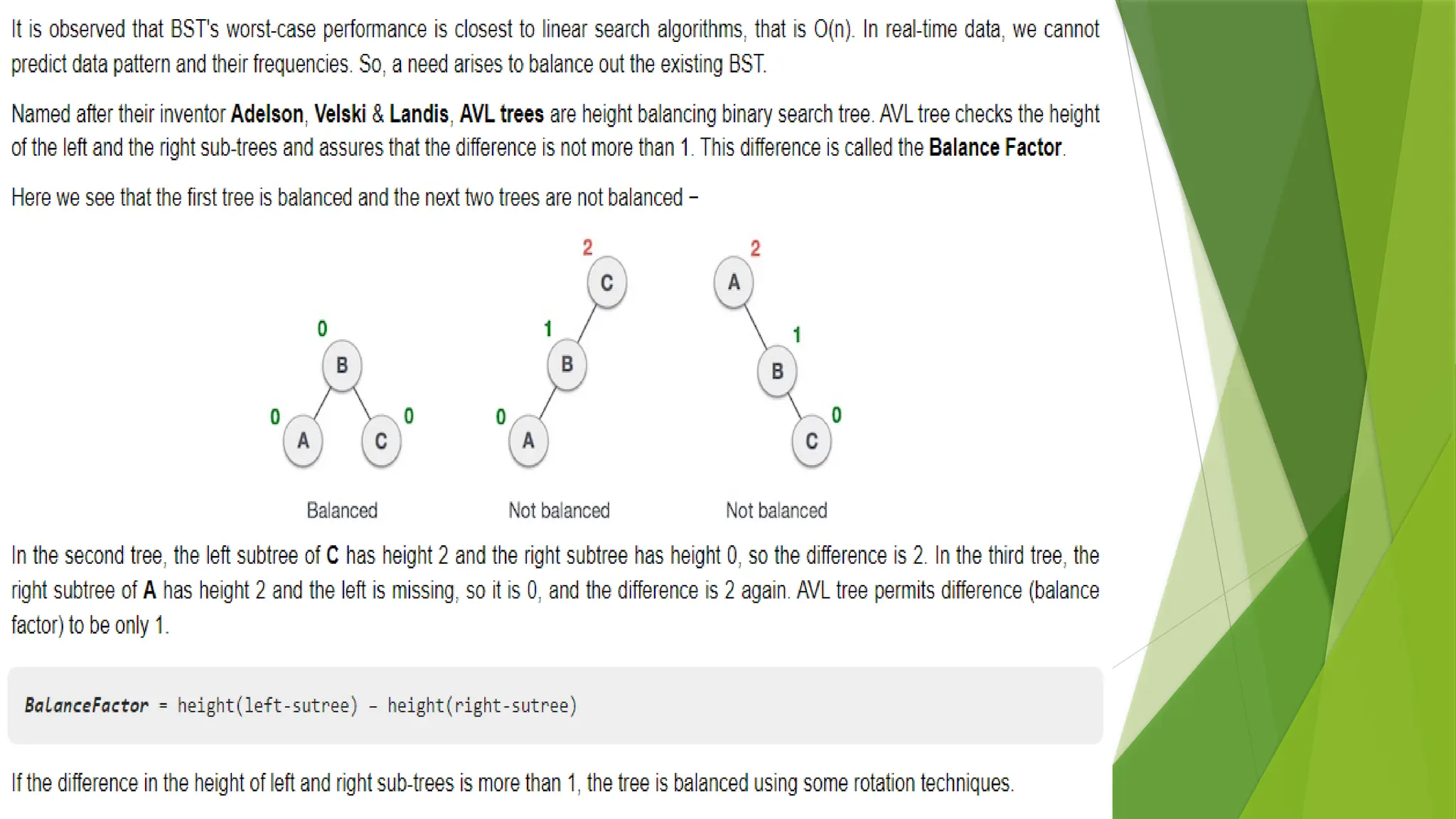
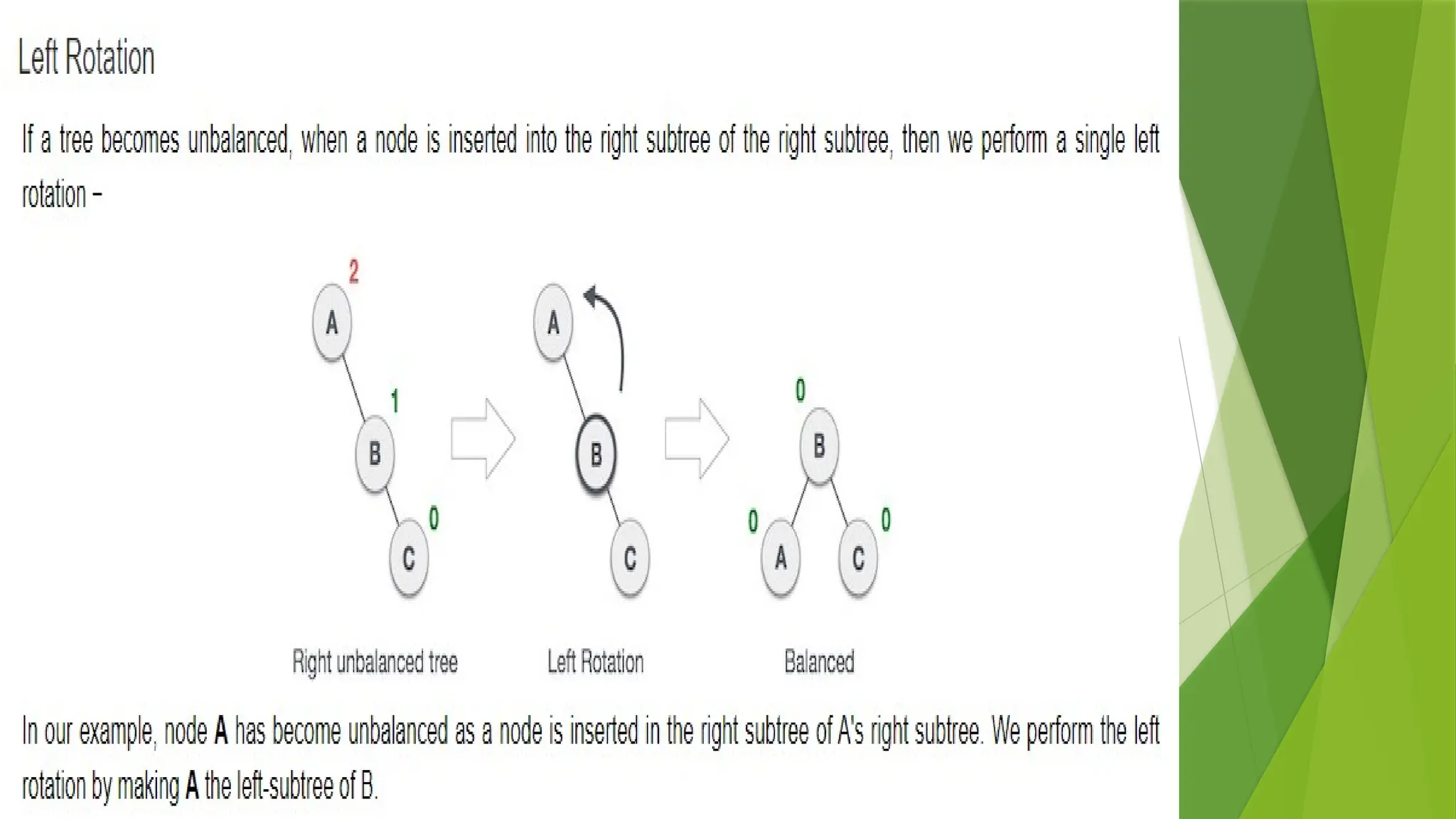
7. Implement an algorithm to check if a BST is height-balanced. If not, convert it into a balanced BST and evaluate
the impact on performance.
8. Write a program to check if a binary tree is a balanced binary tree.
9. Write a function to calculate the height of a binary tree.
10.Implement a program to count the total number of nodes in an AVL tree.