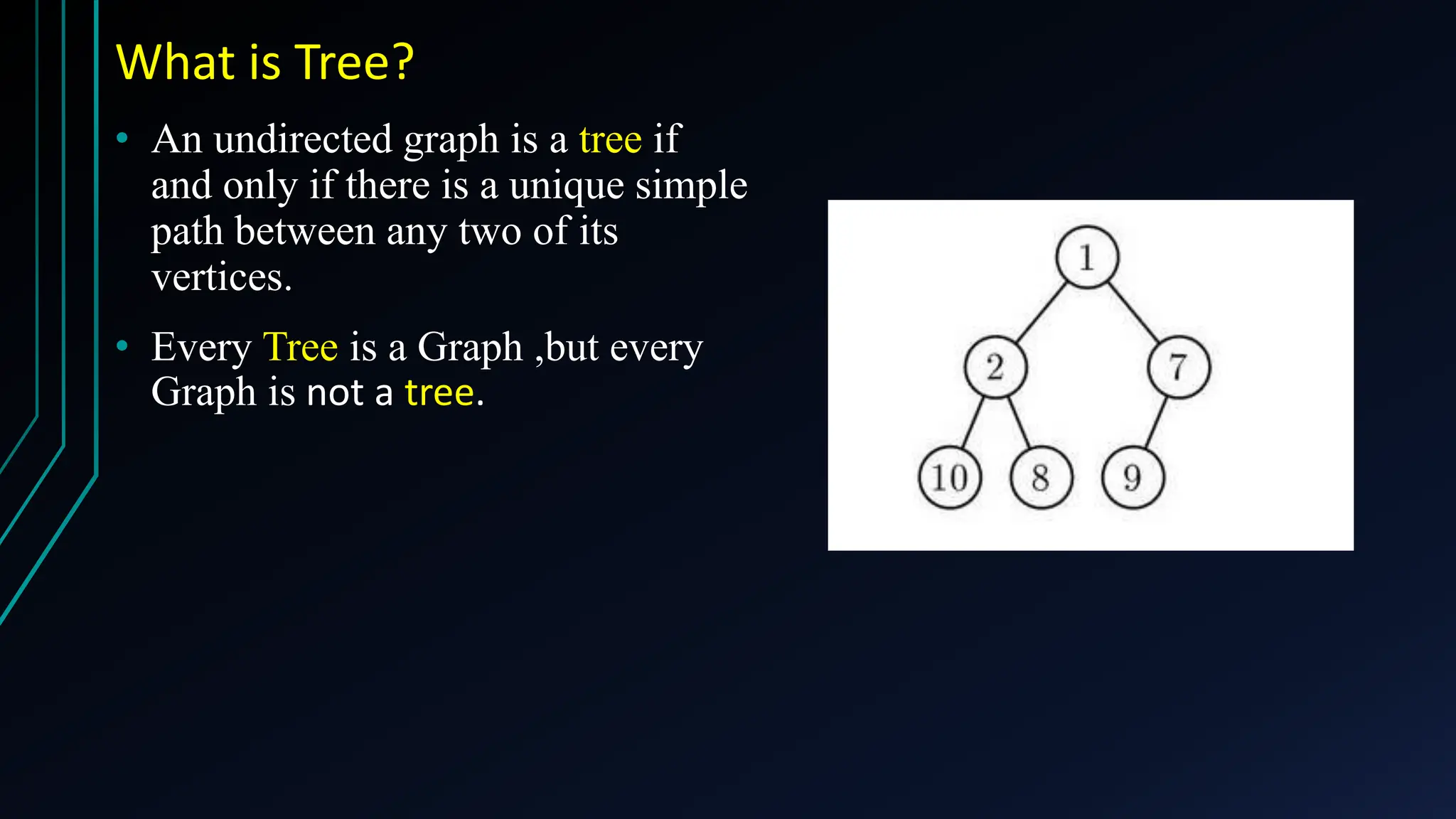
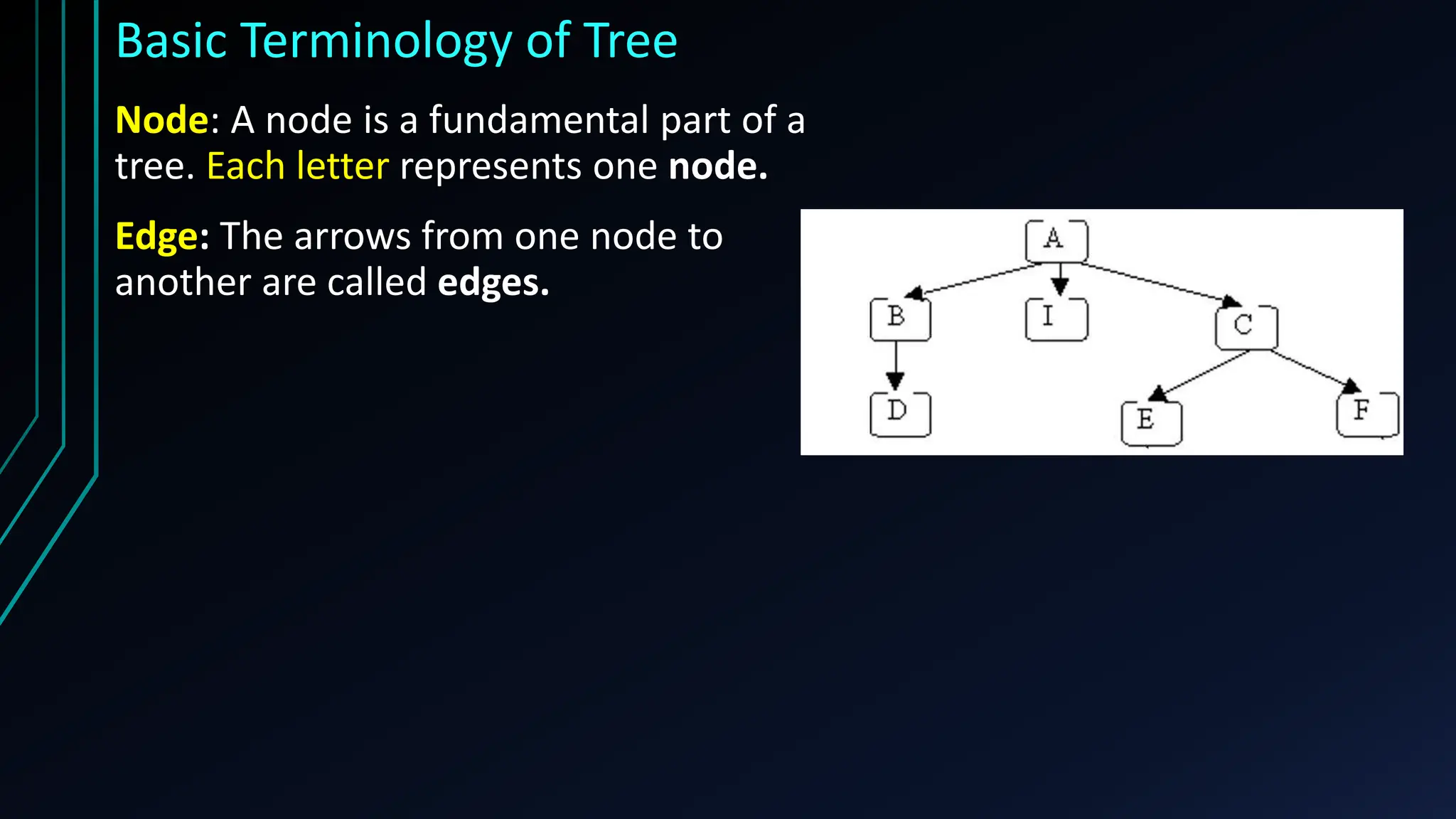
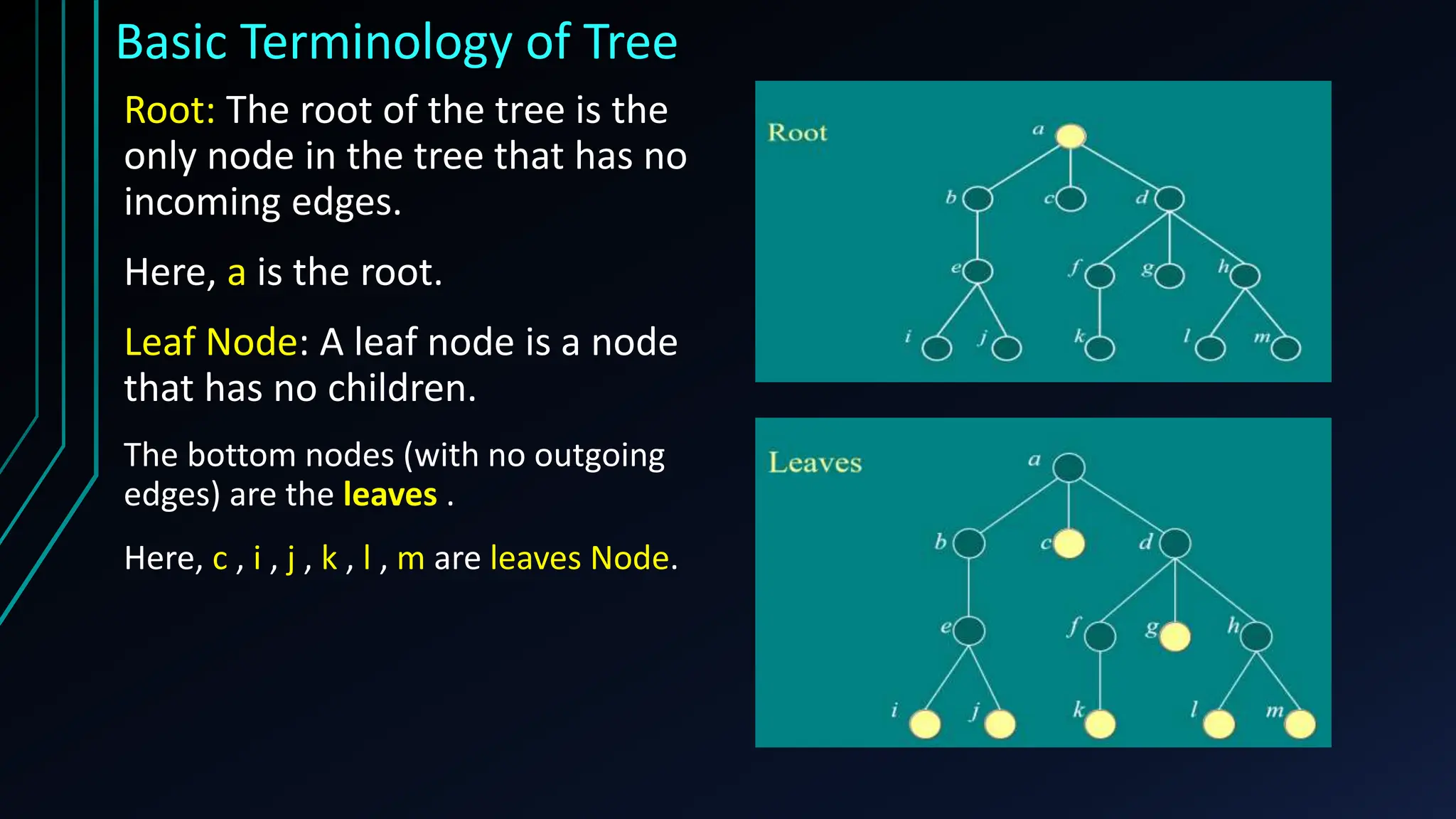
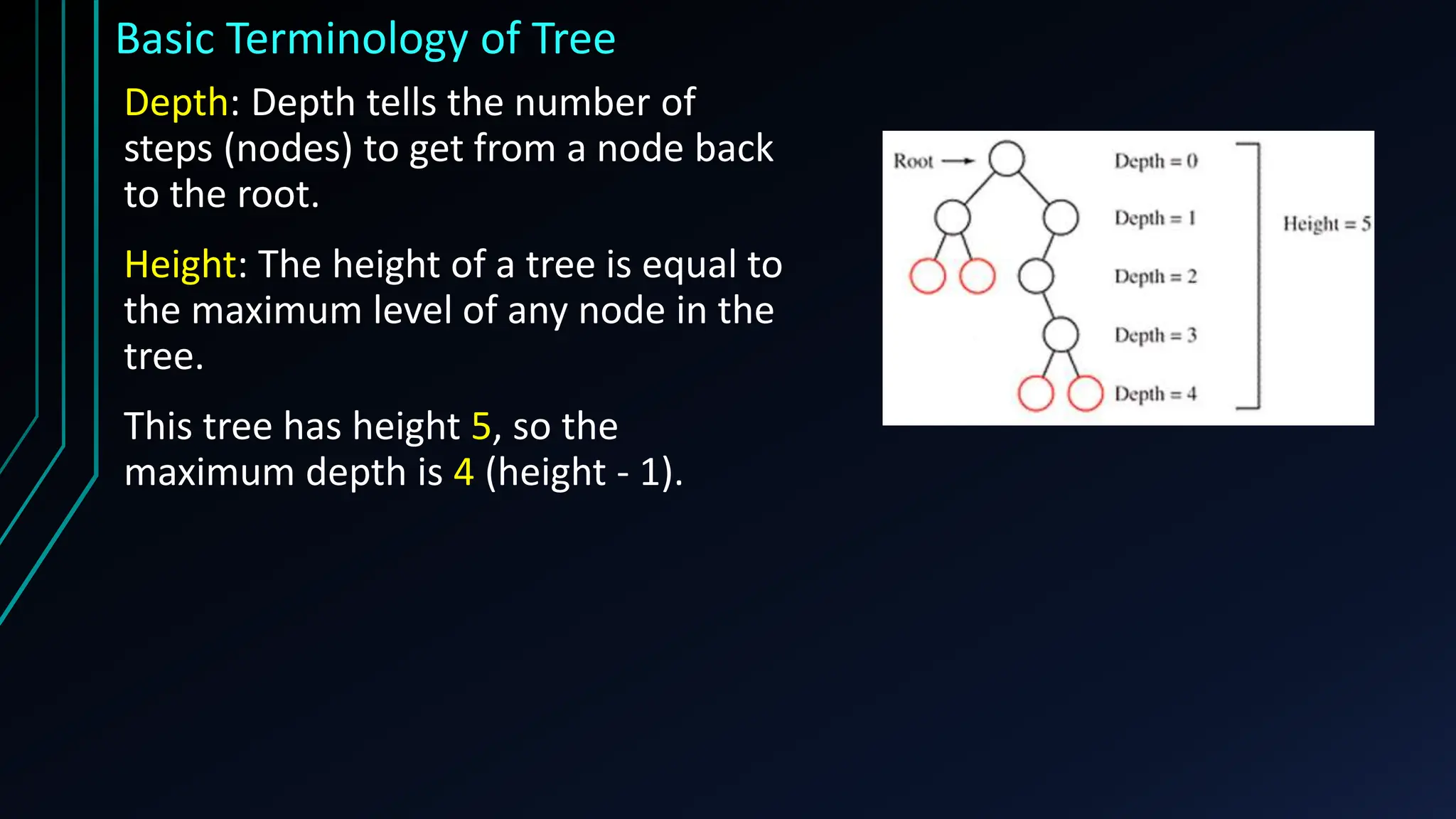
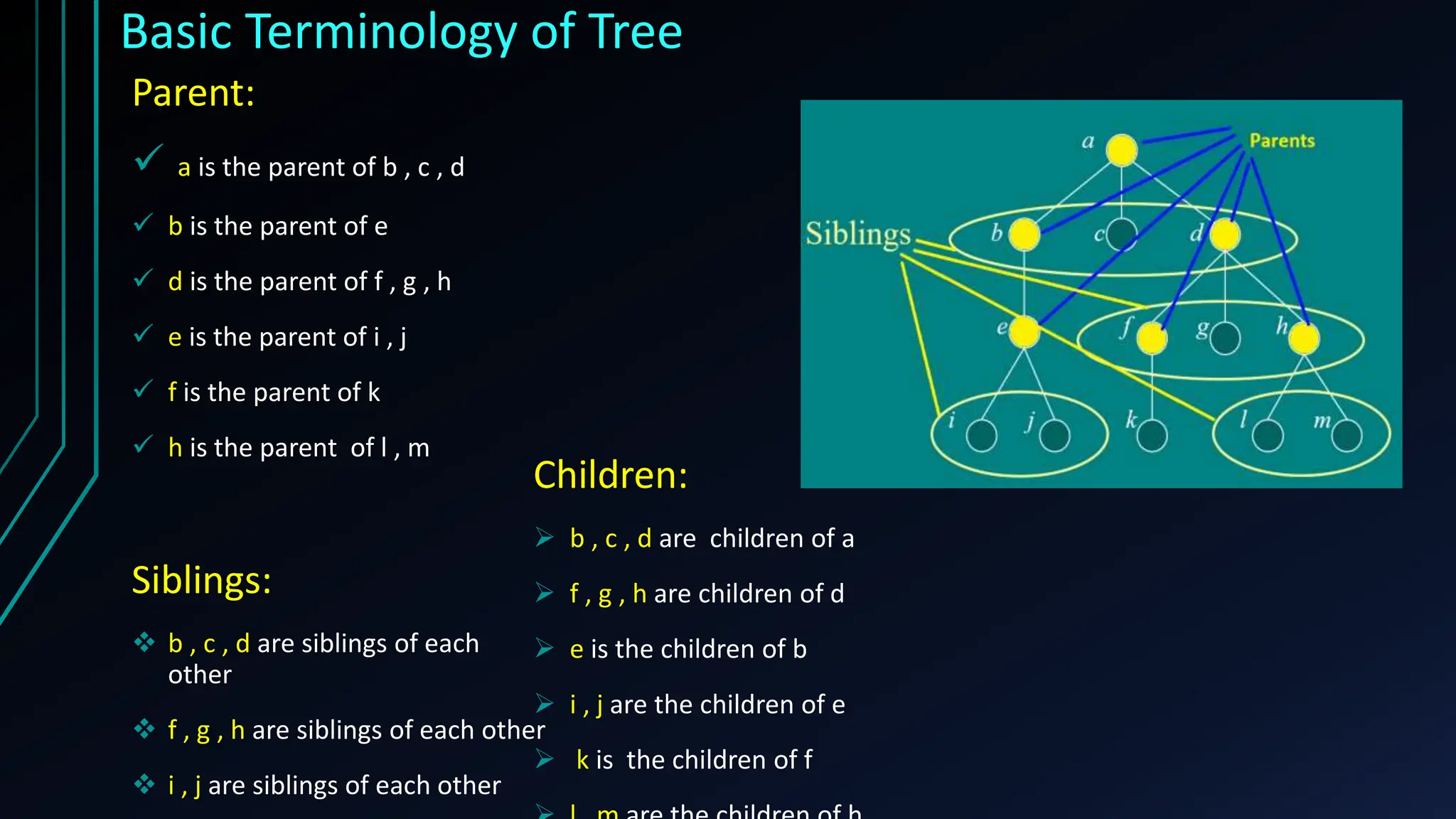
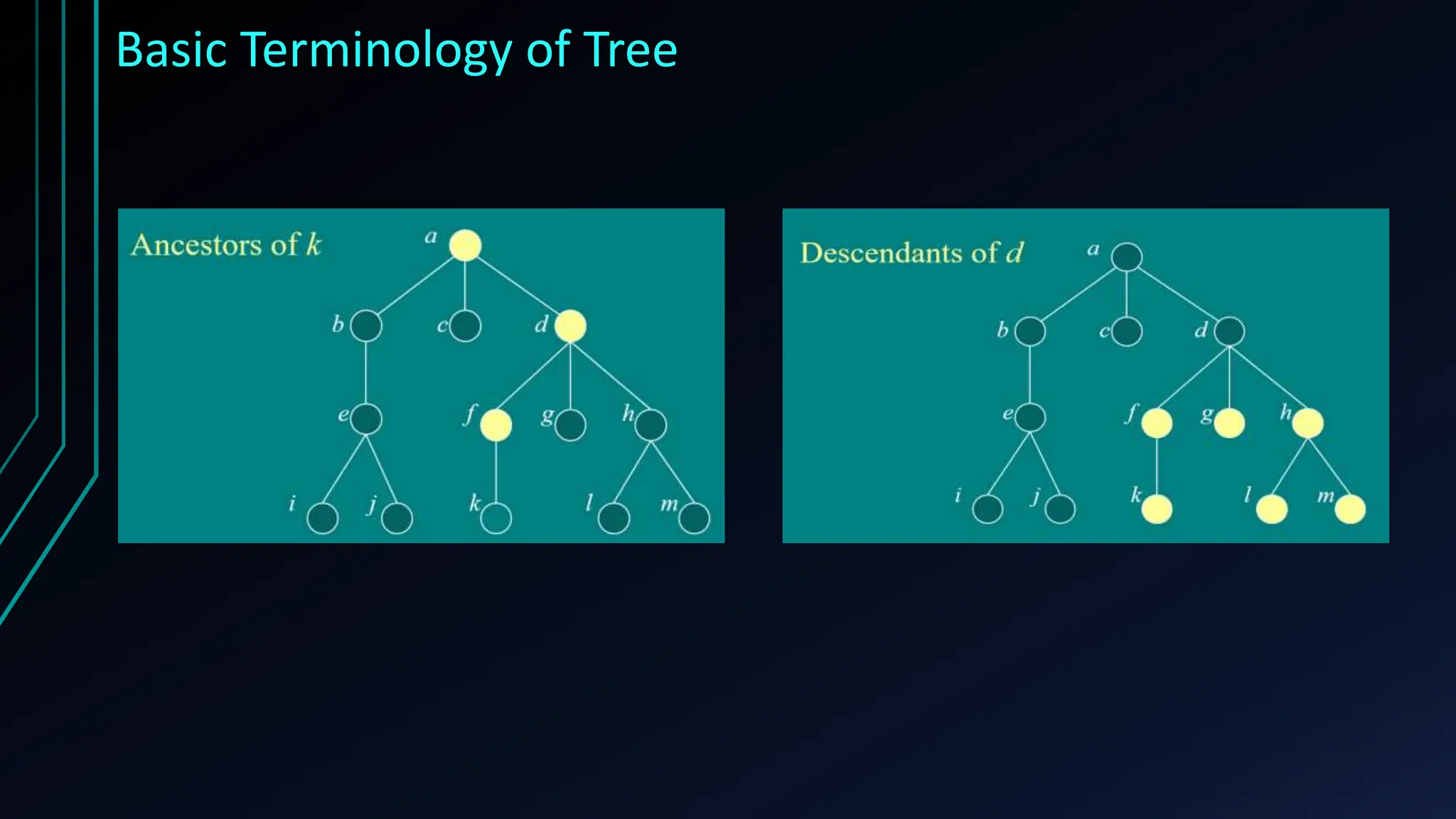
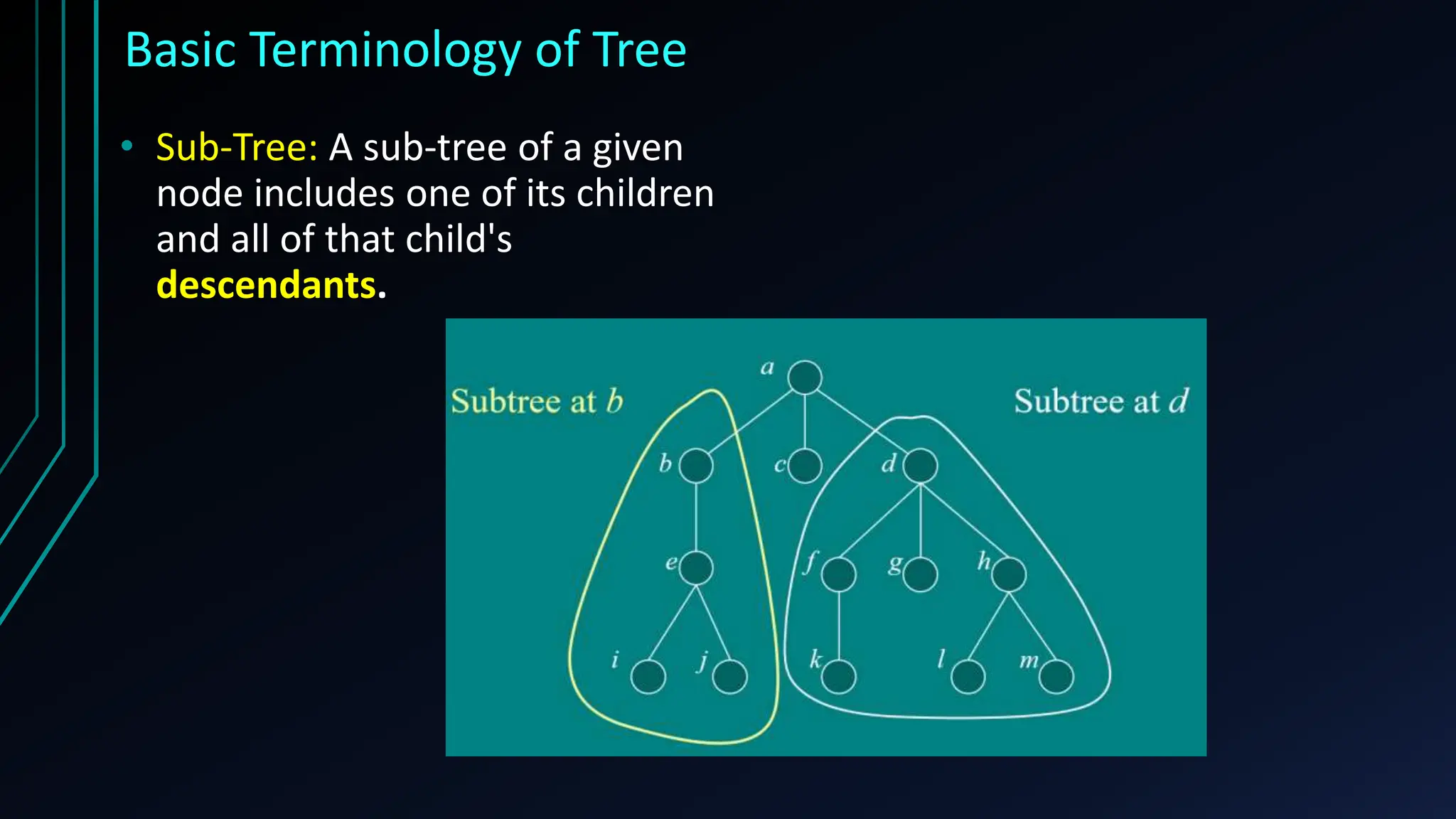
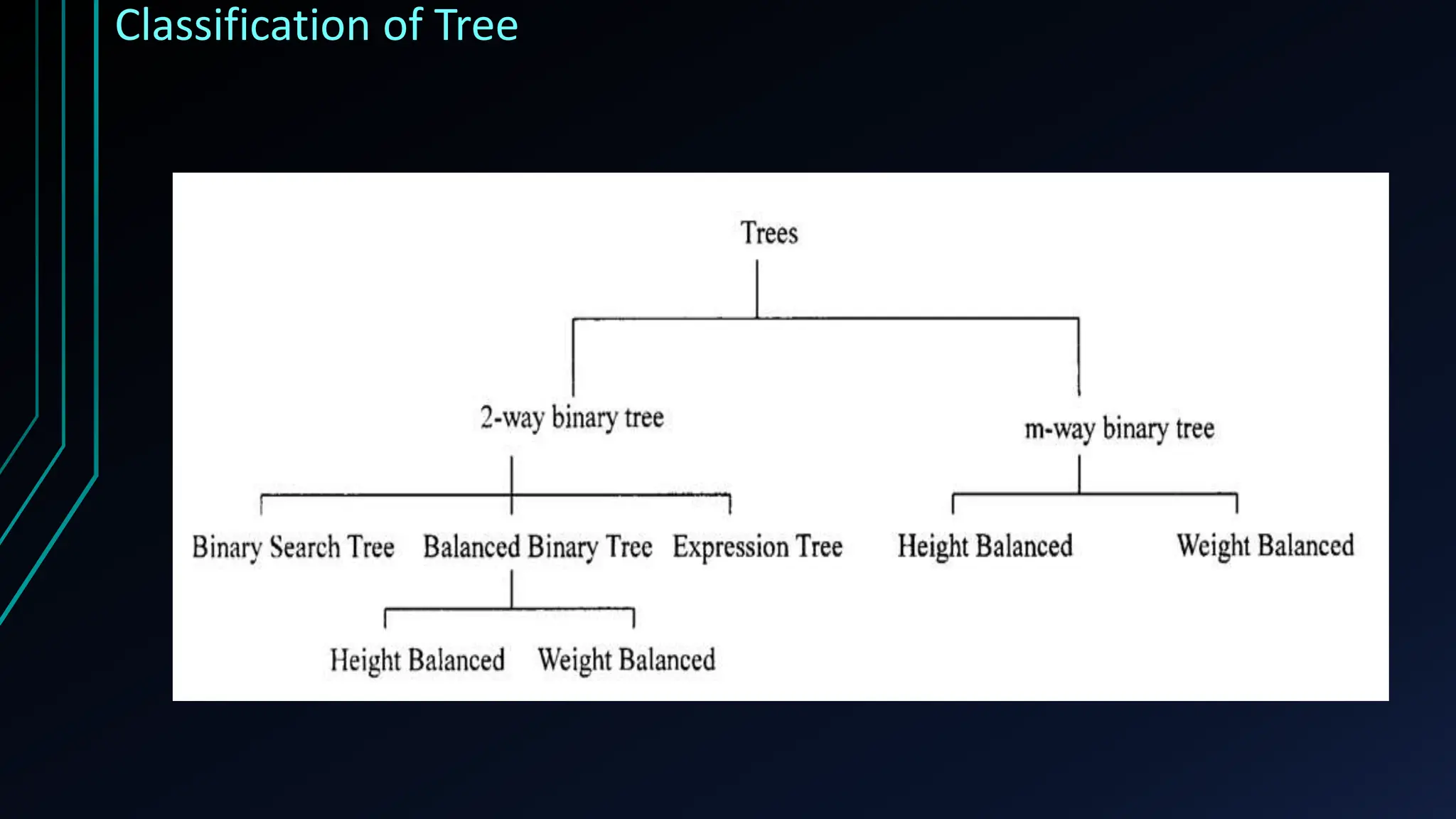
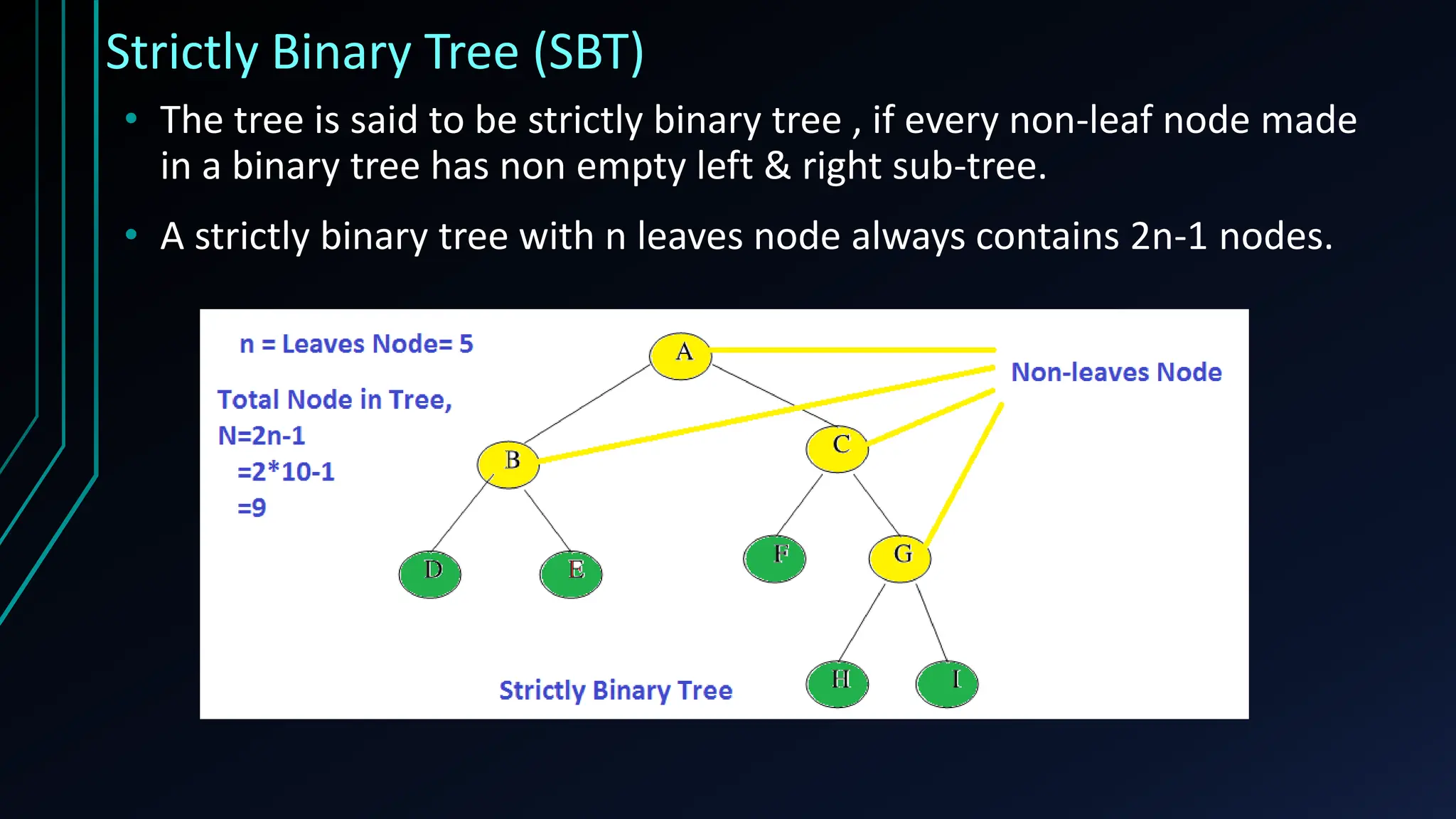
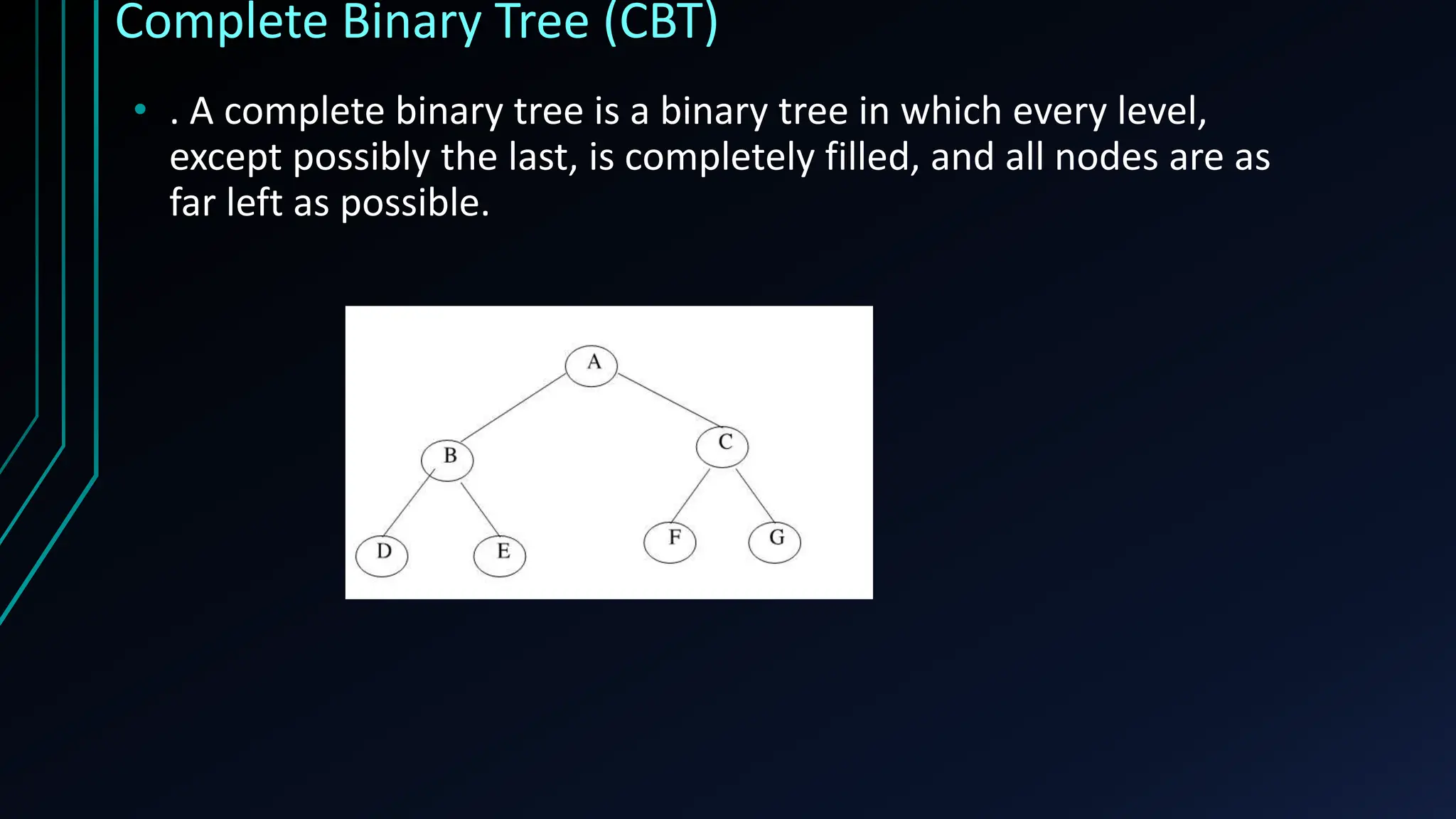
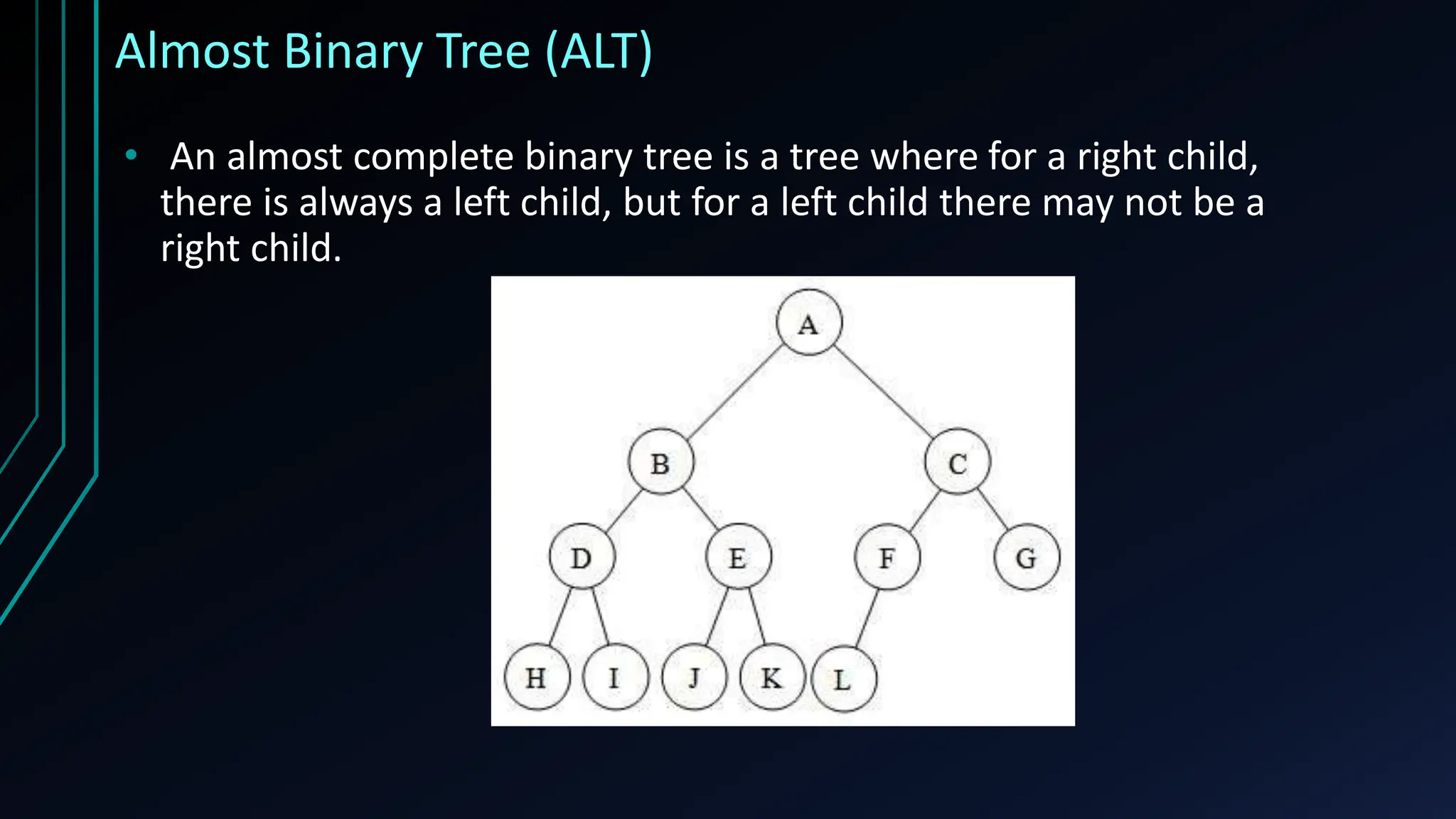
The document provides a comprehensive overview of trees in discrete mathematics, covering their definitions, basic terminology, and classifications such as m-ary, binary, and complete binary trees. It highlights key concepts like nodes, edges, depth, and height, as well as applications of trees in areas like file systems, databases, and artificial intelligence. Understanding trees is crucial for efficiently solving computational problems.

1. Title Layout
• Subtitle

2. Course: CSE131 (Discrete Mathematics)
Course Teacher:
Section: P Group: A
Group Members:

3. Going to Tell About…….
Definition of Tree
Basic Terminology of Tree
Classification of Tree
M-ary Tree
Full M-ary Tree
Binary Tree
Strictly Binary Tree (SBT)
Complete Binary Tree (CBT)
Almost Binary Tree (ALT)
 Application of trees

4. What is Tree?
• An undirected graph is a tree if
and only if there is a unique simple
path between any two of its
vertices.
• Every Tree is a Graph ,but every
Graph is not a tree.

5. Basic Terminology of Tree
 Node
 Edge
 Root
 Leaf Node
 Depth
 Height
 Parent
 Children
 Siblings
 Ancestors
 Descendants
 Sub-Tree

6. Basic Terminology of Tree
Node: A node is a fundamental part of a
tree. Each letter represents one node.
Edge: The arrows from one node to
another are called edges.

7. Basic Terminology of Tree
Root: The root of the tree is the
only node in the tree that has no
incoming edges.
Here, a is the root.
Leaf Node: A leaf node is a node
that has no children.
The bottom nodes (with no outgoing
edges) are the leaves .
Here, c , i , j , k , l , m are leaves Node.

8. Basic Terminology of Tree
Depth: Depth tells the number of
steps (nodes) to get from a node back
to the root.
Height: The height of a tree is equal to
the maximum level of any node in the
tree.
This tree has height 5, so the
maximum depth is 4 (height - 1).

9. Basic Terminology of Tree
Parent:
 a is the parent of b , c , d
 b is the parent of e
 d is the parent of f , g , h
 e is the parent of i , j
 f is the parent of k
 h is the parent of l , m
Siblings:
 b , c , d are siblings of each
other
 f , g , h are siblings of each other
 i , j are siblings of each other
Children:
 b , c , d are children of a
 f , g , h are children of d
 e is the children of b
 i , j are the children of e
 k is the children of f

10. Basic Terminology of Tree

11. Basic Terminology of Tree
• Sub-Tree: A sub-tree of a given
node includes one of its children
and all of that child's
descendants.

12. Classification of Tree

13. m-ary tree : A rooted tree is
called an m-ary tree if every
internal vertex has no more than
m children.
full m-ary tree :A tree is called a
full m-ary tree if every internal
vertex has exactly m children.
binary tree :An m-ary tree with
m  2 is called a binary tree

14. Strictly Binary Tree (SBT)
• The tree is said to be strictly binary tree , if every non-leaf node made
in a binary tree has non empty left & right sub-tree.
• A strictly binary tree with n leaves node always contains 2n-1 nodes.

15. Complete Binary Tree (CBT)
• . A complete binary tree is a binary tree in which every level,
except possibly the last, is completely filled, and all nodes are as
far left as possible.

16. Almost Binary Tree (ALT)
• An almost complete binary tree is a tree where for a right child,
there is always a left child, but for a left child there may not be a
right child.

17. Applications of Trees
Trees find applications in numerous domains:
* File systems: Represent directory structures.
* Databases: Index data for efficient retrieval.
* Network routing: Determine optimal paths between nodes.
* Compilers: Parse code and generate syntax trees.
* Artificial intelligence: Decision trees, game trees.
* Data compression: Huffman coding.
* Sorting and searching algorithms: Heap sort, binary search trees.
Conclusion
Trees are a fundamental data structure with a wide range of
applications. Understanding their structure and properties is essential
for solving various computational problems efficiently.