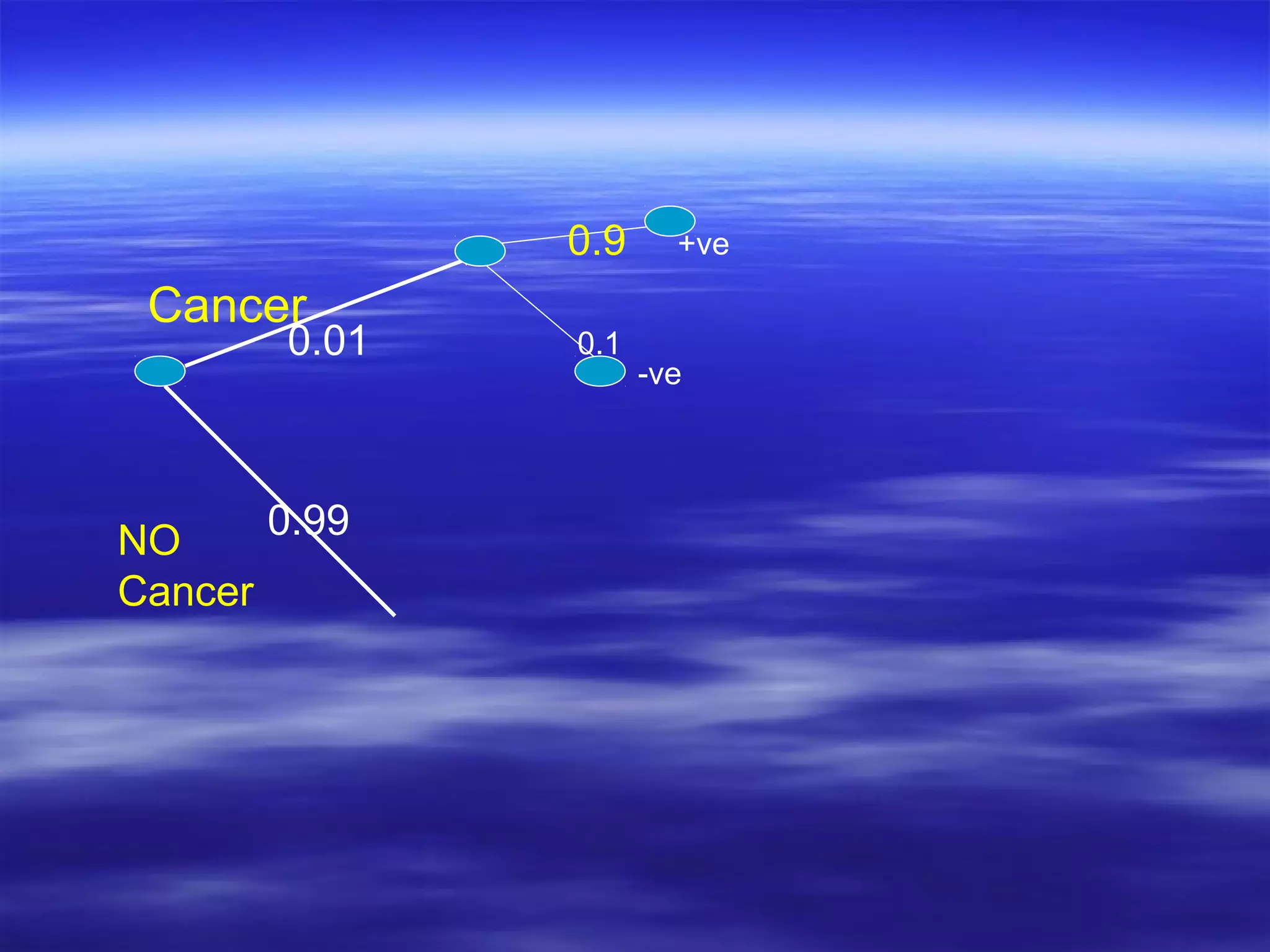
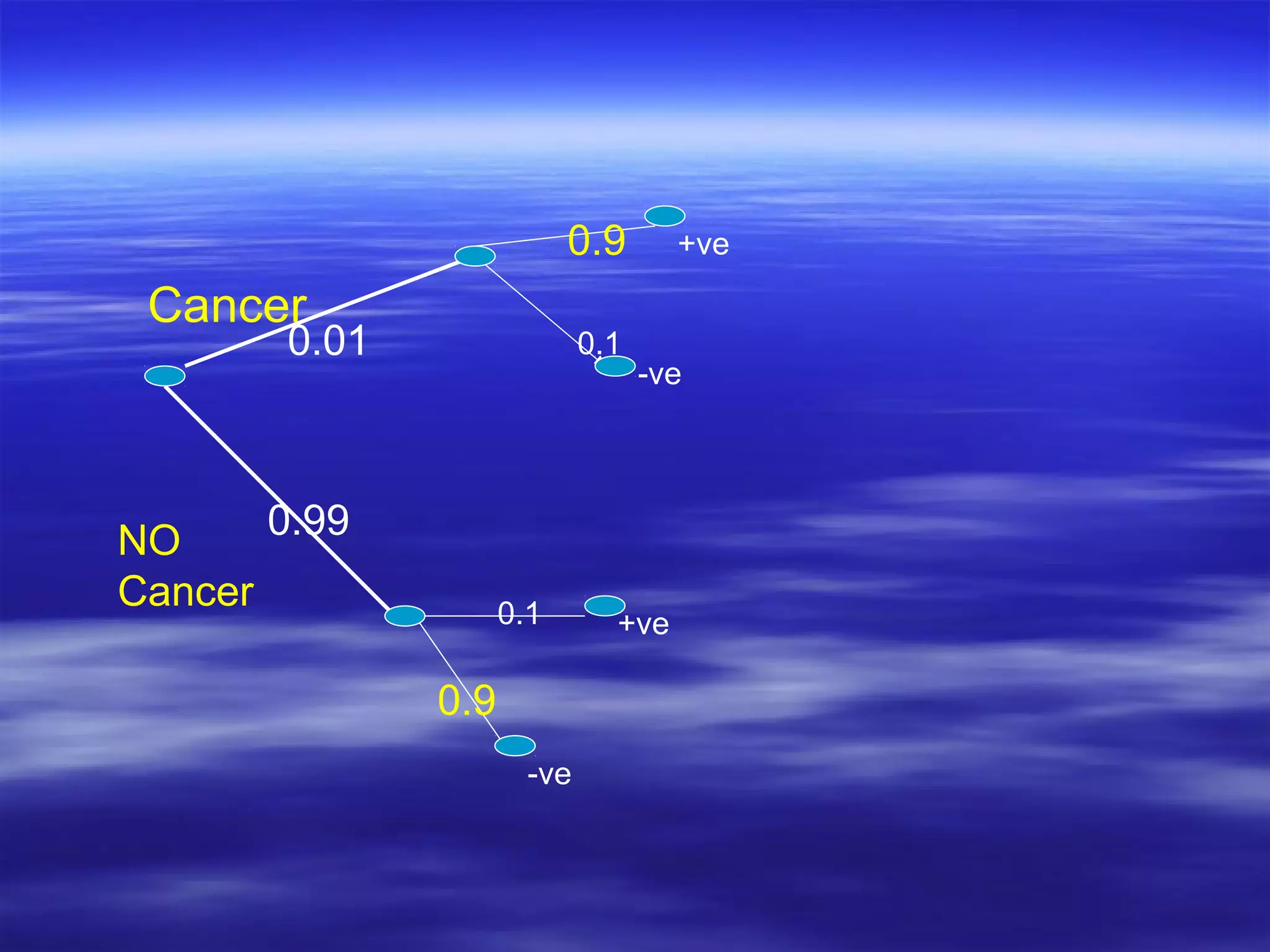
The document discusses probability and key concepts in probability theory such as conditional probability and Bayes' theorem. Some key points: - Probability is a quantitative expression of the likelihood of an event occurring, defined as the number of times an event occurs divided by the total number of times it can occur. - Conditional probability measures the probability of an event given that another event has occurred. - Bayes' theorem applies conditional probability to update probabilities based on additional information obtained. It relates the posterior probability to the prior probability. - Examples show how to calculate probabilities of complex events using rules like the multiplication rule and addition rule. 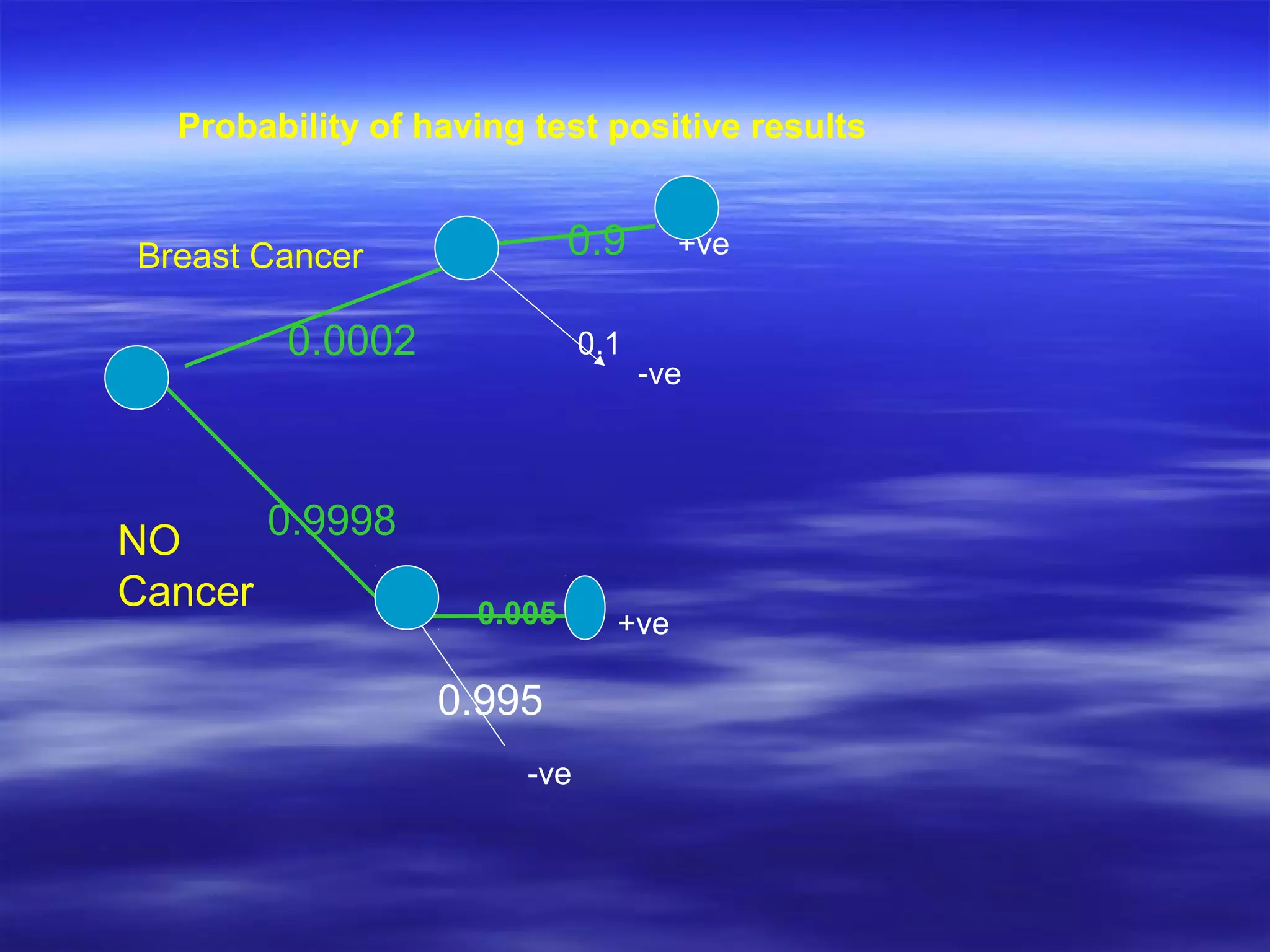- Bayes' theorem is used to calculate the probability of a disease given a positive test result, taking

1. ProbabilityProbability
Prof. Khaled MahmoudProf. Khaled Mahmoud
Associate ProfessorAssociate Professor
Department of community, EnvironmetnalDepartment of community, Environmetnal
and occupational medicine,and occupational medicine,
Faculty of Medicine, Ain Shams UniversityFaculty of Medicine, Ain Shams University

2.  The probability of an event is a quantitativeThe probability of an event is a quantitative
expression of the likelihood of itsexpression of the likelihood of its
occurrenceoccurrence
 Pr (A)=Pr (A)= number of times A does occurnumber of times A does occur
total no. of times A can occurtotal no. of times A can occur

3.  Example: in food outbreak. 158 peopleExample: in food outbreak. 158 people
attendedattended a banquet. The probability ofa banquet. The probability of
illness for a person selected at random isillness for a person selected at random is
 Pr (illness)=Pr (illness)= 99 =99 = 0.63 or 63%0.63 or 63%
158158
Probability can be expressed in fractions,Probability can be expressed in fractions,
decimals, decimal fractionsm must fall in thedecimals, decimal fractionsm must fall in the
range of 0 to 1 so thatrange of 0 to 1 so that

4.  Pr (illness)=Pr (illness)= 99 =99 = 0.63 or 63%0.63 or 63%
158158
Probability can be expressed in fractions, decimals,Probability can be expressed in fractions, decimals,
decimal fractions must fall in the range of 0 to 1decimal fractions must fall in the range of 0 to 1
so thatso that
Pr (event A does not occur)=1-Pr (event A occurs)Pr (event A does not occur)=1-Pr (event A occurs)
Pr (illness does not occur) = 1- 0.63 = 0.37 or 37%Pr (illness does not occur) = 1- 0.63 = 0.37 or 37%

5. Conditional probabilityConditional probability ‫الشرطى‬ ‫التحتمال‬‫الشرطى‬ ‫التحتمال‬
conditional probability measures theconditional probability measures the
probability of an event given that (byprobability of an event given that (by
assumption, presumption, assertion orassumption, presumption, assertion or
evidence) another event has occurredevidence) another event has occurred
In food poisoning example the probability of aIn food poisoning example the probability of a
given person becomes ill was 0.63given person becomes ill was 0.63

6.  The probability of illness can be modified ifThe probability of illness can be modified if
we knew the food the person ate.we knew the food the person ate.
 Pr (A| B)=Pr (A| B)= number of times A and B occur jointlynumber of times A and B occur jointly
total no. of times B occurtotal no. of times B occur
Pr (Illness| turkey)=Pr (Illness| turkey)= number who ate turkey and became illnumber who ate turkey and became ill
number of people who ate turkeynumber of people who ate turkey
== 97 =97 = 0.73 or 73%0.73 or 73%
133133
So the probability of getting illness if the subject consumesSo the probability of getting illness if the subject consumes
turkey is 73%turkey is 73%

7.  Complex eventsComplex events
 Events expressed as specific combination AEvents expressed as specific combination A
and B, Expressed as specified alternativesand B, Expressed as specified alternatives
A or BA or B
 Pr (A and B)= probability that A and B occurPr (A and B)= probability that A and B occur
jointlyjointly
 Pr (A or B)= probability that A occurs or BPr (A or B)= probability that A occurs or B
occurs= probability that at least one of theoccurs= probability that at least one of the
stated alternatives will occurstated alternatives will occur

8.  Multiplication RuleMultiplication Rule
 Pr ( A and B) = Pr (A) X Pr (B)Pr ( A and B) = Pr (A) X Pr (B)
ExampleExample
Side effects of certain drug occurs in 10% of allSide effects of certain drug occurs in 10% of all
patients who take it. A physician has 2 patientspatients who take it. A physician has 2 patients
who are taking the drug. What is the probabilitywho are taking the drug. What is the probability
that both will experience side effectsthat both will experience side effects
The events are independent, that is the occurrenceThe events are independent, that is the occurrence
of side effects in one patient does not affect theof side effects in one patient does not affect the
likelihood of side effects in the other patient.likelihood of side effects in the other patient.

9.  Multiplication RuleMultiplication Rule
 Pr ( A and B) = Pr (A) X Pr (B)Pr ( A and B) = Pr (A) X Pr (B)
 Pr of both patients experience side effectsPr of both patients experience side effects
 Pr (A and B)= 0.1 X0.1 =0.01Pr (A and B)= 0.1 X0.1 =0.01
 So the probability of both patients A and BSo the probability of both patients A and B
will experience side effects is 1%will experience side effects is 1%

10.  Addition RuleAddition Rule
 Pr ( A or B) = Pr (A) + Pr (B)- Pr ( A and B)Pr ( A or B) = Pr (A) + Pr (B)- Pr ( A and B)
ExampleExample
What is the probability that at least one of theWhat is the probability that at least one of the
patients experiences side effects.patients experiences side effects.
Pr (A or B)= 0.1 +0.1-0.01= 0.19 or 19%Pr (A or B)= 0.1 +0.1-0.01= 0.19 or 19%
So the probability that at least one patient willSo the probability that at least one patient will
experience side effects is 19%experience side effects is 19%

11.  Bayes TheoremBayes Theorem
 Application of conditional probability basedApplication of conditional probability based
on additional information that is lateron additional information that is later
obtained. Dealing with sequential eventsobtained. Dealing with sequential events
 Priori probabilityPriori probability: is an initial probability: is an initial probability
originally obtained before any additionaloriginally obtained before any additional
information is obtainedinformation is obtained
 Posterior probabilityPosterior probability: is the probability value: is the probability value
that has been revised by using additionalthat has been revised by using additional
information that is later obtainedinformation that is later obtained

12.  Diagnosis a problemDiagnosis a problem
 Application of certain clinical test toApplication of certain clinical test to
diagnose cancer cervix .diagnose cancer cervix .
 The test is 90% sensitiveThe test is 90% sensitive
 The prevalence rate of the disease is 1% inThe prevalence rate of the disease is 1% in
the same age group as the patientthe same age group as the patient
 The test has a false positive 10%The test has a false positive 10%

13.  Bayes TheoremBayes Theorem
 Pr (A |B) =Pr (A |B) = Pr (B|A) X P(A)Pr (B|A) X P(A)
Pr (B)Pr (B)
Pr (cancer| +)=Pr (cancer| +)= P (+ | cancer) X P (cancer)P (+ | cancer) X P (cancer)
P (+)P (+)

14. Cancer
NO
Cancer
0.01
0.99

15. Cancer
NO
Cancer
0.01
0.99
+ve
-ve
0.9
0.1

16. Cancer
NO
Cancer
0.01
0.99
+ve
-ve
0.9
0.1
+ve
-ve
0.1
0.9

17. Cancer
NO
Cancer
0.01
0.99
+ve
-ve
0.9
0.1
+ve
-ve
0.1
0.9
Probability of having test positive results

18.  Bayes TheoremBayes Theorem
 Pr (A |B) =Pr (A |B) = Pr (B|A) X P(A)Pr (B|A) X P(A)
Pr (B)Pr (B)
Pr (cancer| +)=Pr (cancer| +)= (0.9) X (0.01)(0.9) X (0.01)
(0.01)(0.9) + (0.99)(0.1)(0.01)(0.9) + (0.99)(0.1)

19.  Bayes TheoremBayes Theorem
Pr (cancer| +)=Pr (cancer| +)= (0.009)(0.009)
(0.009) + (0.099)(0.009) + (0.099)
= 0.009/0.108 = 9/108 = 0.083= 0.009/0.108 = 9/108 = 0.083
=8.3%=8.3%
So the probability that the subject has a breastSo the probability that the subject has a breast
cancer after doing the test and being positive iscancer after doing the test and being positive is
only 8.3%only 8.3%

20.  Diagnosis a problemDiagnosis a problem
 Application of certain clinical test to diagnoseApplication of certain clinical test to diagnose
breast cancer .breast cancer .
 The test is 90% sensitiveThe test is 90% sensitive
 The prevalence rate of the disease is 1/5000The prevalence rate of the disease is 1/5000
(0.0002)in the same age group as the patient(0.0002)in the same age group as the patient
 The test has a false positive 0.005 5 positiveThe test has a false positive 0.005 5 positive
results in every 1000 women who don’t have theresults in every 1000 women who don’t have the
disease.disease.

21. Breast Cancer
NO
Cancer
0.0002
0.9998
+ve
-ve
0.9
0.1
+ve
-ve
0.005
0.995
Probability of having test positive results

22.  Pr (A |B) =Pr (A |B) = Pr (B|A) X P(A)Pr (B|A) X P(A)
Pr (B)Pr (B)
Pr (cancer| +)=Pr (cancer| +)= (0.9) X (0.0002)(0.9) X (0.0002)
0.9X0.0002 + (0.9998)(0.005)0.9X0.0002 + (0.9998)(0.005)
Pr (cancer|+)= 0.00018/0.005179= 0.0348Pr (cancer|+)= 0.00018/0.005179= 0.0348
=3.48%=3.48%

23. THANK YOU