Thiết kế máy công cụ

Bµi gi¶ng
thiÕt kÕ m¸y C«NG Cô

CH¦¥NG 1
ThiÕt kÕ ®éng häc m¸y c¾t kim lo¹i
1. Lý thuyÕt vÒ chuçi sè vßng quay
vµ ch¹y dao trong m¸y
2. ThiÕt kÕ truyÒn dÉn hép tèc ®é
3. ThiÕt kÕ truyÒn dÉn hép ch¹y dao

3
Ph©n lo¹i truyÒn dÉn:
TruyÒn dÉn v« cÊp: Cho trÞ sè tèc ®é bÊt kú trong
ph¹m vi biÕn ®æi tèc ®é (hay l-îng ch¹y dao) –
trong m¸y mµi, m¸y CNC.
TruyÒn dÉn ph©n cÊp: M¸y cã mét sè l-îng h÷u
h¹n tèc ®é c¾t hay l-îng ch¹y dao. VÝ dô trªn m¸y
tiÖn T620 cã 23 tèc ®é: tõ 12,5  2000 v/p.
 VËn tèc:
D : ®-êng kÝnh chi tiÕt (mm)
n : Sè vßng quay (v/ph)
( / )
1000
Dn
v m ph


1. Lý thuyÕt vÒ chuçi sè vßng quay vµ ch¹y Dao

4
Coi V lµ hµm sè cña biÕn D, tham sè n vÏ ®-îc ®å
thÞ quan hÖ V, n, D:

5
 Víi mçi D0  chän ®-îc chÕ ®é c¾t hîp lý theo:
VËt liÖu dao, vËt liÖu ph«i
§é chÝnh x¸c gia c«ng
§iÒu kiÖn gia c«ng
Tõ V0, D0  n0
 nhîp lý = n0  Vhîplý = V0
V× truyÒn dÉn ph©n cÊp  Vk <V0<Vk+1
Th-êng chän V0 = Vk  cã tæn thÊt tèc ®é:
V=V0-Vk (tuyÖt ®èi)

6
 Tæn thÊt t-¬ng ®èi:
 Tæn thÊt ®ã thay ®æi tuy cã cïng D0
 Tæn thÊt lín nhÊt khi: V0  Vk+1:
 Mong muèn tæn thÊt cùc ®¹i Vmax = const:
%100.
0
0
V
VV
V k

0 1
0
max
0
lim .100%
k
k
V V
V V
V
V

 
1
max
1 1
.100% 1k k k
k k
V V V
V const
V V

 

    

8
1 1
k k
k k
V n
const
V n 
  
 Chuçi sè vßng quay ph¶i lµ mét cÊp sè nh©n, cã
c«ng béi lµ  = nk+1/nk
C«ng béi :
Chuçi sè vßng quay lµ cÊp sè nh©n tiÕn:  >1
V× Vmax  50%
 2501001
1


%%).
V
V
(
k
k
1 2  

9
XÐt tr-êng hîp tiÖn chi tiÕt chiÒu dµi L. Cho chÕ
®é c¾t: n(v/ph) vµ S(mm/v)
 Thêi gian tiÕn dao S: 1/n(ph)
 Thêi gian gia c«ng xong mét chi tiÕt: L/n.S(ph)
Ta l¹i cã: n¨ng suÊt Q = 1/tct (ct/ph)
Q = n.S/L (ct/ph)
Q0 = n0.S/L (ct/ph)
T-¬ng tù ta cã tæn hao n¨ng suÊt:
 Sè vßng quay theo cÊp sè nh©n th× tæn hao n¨ng
suÊt cùc ®¹i còng b»ng h»ng sè
const%).
n
n
(Q
k
k
max 

1001
1

10
TrÞ sè c«ng béi  ®-îc tiªu chuÈn hãa. Tuú theo
tÝnh chÊt sö dông cña mçi lo¹i m¸y mµ ng-êi ta
chän  kh¸c nhau.
Çc nguyªn t¾c thµnh lËp gi¸ trÞ  tiªu chuÈn:
Nguyªn t¾c gÊp 10: çch qu·ng x sè h¹ng th×
nx+1=10n1; v× nx+1=n1.x  x = 10
Nguyªn t¾c gÊp 2: çch qu·ng y sè h¹ng th×
ny+1=2n1; v× ny+1 = n1.y  y =2
yx
210 

11
 TrÞ sè
 B¶ng trÞ sè  tiªu chuÈn:
1240
210061  ,min
x
10 y
2
TrÞ sè 
=1,06E
Vmax(%)
E x y
1,06
1,12
1,26
1,41
1,58
1,78
2,00
1
2
4
6
8
10
12
40
20
10
20/3
5
4
20/6
12
6
3
2
3/2
-
1
5%
10%
20%
30%
40%
45%
50%

12
 Ph¹m vi sö dông çc trÞ sè  tiªu chuÈn:
  = 1,06 Ýt dïng v× chuçi sè dµy ®Æc
  = 1,12  dïng cho çc m¸y tù ®éng (cÇn
chÕ ®é c¾t chÝnh x¸c, Ýt tæn thÊt n vµ Q)
  = 1,26 vµ  = 1,41  dïng cho çc m¸y v¹n
n¨ng
  = 1,58 vµ  = 1,78  dïng cho çc m¸y cã
tct<tck
  = 2  Ýt dïng, cã ý nghÜa trong tÝnh to¸n
nhãm khuyÕch ®¹i trong HT§, hoÆc nhãm gÊp
béi trong HCD

13
 TrÞ sè vßng quay tiªu chuÈn c¬ së: (thµnh lËp tõ
= 1,06; n1 = 1(vg/ph); nz = n1. z-1)
1 – 1,06 – 1,12 – 1,18 – 1,25 – 1,32 – 1,41
–
1,5 – 1,6 – 1,7 – 1,8 – 1,9 – 2 – 2,12 – 2,24
–
2,35 – 2,5 – 2,65 – 2,8 – 3 – 3,15 – 3,25 –
3,5 –
3,75 – 4 – 4,25 – 4,5 – 4,75 – 5 –5,3 – 5,6

14
 X¸c ®Þnh çc gi¸ trÞ vßng quay tiªu chuÈn kh¸c
b»ng çch nh©n çc trÞ sè vßng quay tiªu chuÈn
c¬ së víi 10x (x: sè nguyªn ©m hay d-¬ng)
 Muèn x¸c ®Þnh chuçi sè vßng quay tiªu chuÈn
c¬ së cã c«ng béi  kh¸c: = E
min  lÊy çch
qu·ng çc trÞ sè n çch nhau E sè h¹ng trong
d·y trªn
VÝ dô:
= 1,26= 1,064  E=4  chuçi sè vßng quay
tiªu chuÈn c¬ së lµ 1 – 1,25 – 1,6 – 2 – 2,5
– 3,35 ...

15
2.1 C«ng dông vµ yªu cÇu cña hép tèc ®é:
Hép tèc ®é truyÒn tèc ®é c¾t cho c¸c chi tiÕt hoÆc
gia c«ng, thiÕt kÕ HT§ ph¶i ®¶m b¶o c¸c yªu cÇu
sau:
KÕt cÊu cã tÝnh c«ng nghÖ cao: dÔ gia c«ng, l¾p
r¸p, thay thÕ, söa ch÷a.
Sö dông dÔ dµng.
KÝch th-íc nhá gän, hiÖu suÊt cao, tiÕt kiÖm vËt
liÖu.
Lµm viÖc chÝnh x¸c, an toµn.
2. ThiÕt kÕ truyÒn dÉn hép tèc ®é

16
 VÒ mÆt tèc ®é c¾t:
§¶m b¶o kho¶ng tèc ®é c¾t: Vmin  Vmax hay
nmin  nmax
Ph¹m vi ®iÒu chØnh tèc ®é:
Smin  Smax 
VÝ dô:
M¸y phay 6H82 cã:
Nmin  nmax = 30  1500 vg/ph
Smin  Smax = 19  1180 mm/ph
max
min
n
n
R
n

max
min
S
S
R
S


17
 VÒ lùc c¾t:
T¸c dông lªn trôc chÝnh cña m¸y, HT§ ph¶i
®¶m b¶o lùc c¾t nµy. Khi gia c«ng c¸c chi tiÕt
kh¸c nhau, yªu cÇu:

18
BR trung gian Z1 cã vÞ trÝ bÊt kú khi ¨n khíp
víi BR Z’
1. Ta sÏ bè trÝ BR Z1 ë vÞ trÝ sao cho
®é vâng y nhá nhÊt.
y = yFc + ybr
y = yFc - ybr

19
 VÒ viÖc sö dông m¸y:
 §iÒu khiÓn HT§ thùc hiÖn dÔ dµng, an toµn
 T¹o ®iÒu kiÖn cho HT§ lµm viÖc víi hiÖu suÊt
cao (gi¶m çc cÆp BR quay kh«ng, tr¸nh dïng
çc truyÒn dÉn cã hiÖu suÊt thÊp)
 Çc chØ tiªu ®¸nh gi¸ chÊt l-îng HT§:
 C«ng suÊt truyÒn dÉn
 Giíi h¹n sè vßng quay nmin  nmax, c«ng béi 
( cµng nhá th× çc tèc ®é cµng gÇn nhau)
 Møc ®é phøc t¹p vµ hiÖu suÊt cña xÝch truyÒn
 Møc ®é ®iÒu khiÓn vµ ®é tin cËy
 TÝnh c«ng nghÖ chÕ t¹o çc chi tiÕt

20
2.2 Hép tèc ®é dïng b¸nh r¨ng di tr-ît:
2.2.1 Ph-¬ng ¸n kh«ng gian.
n®c n1  nZ, cã Z tèc ®é
Gi¶ sö cã Z cÊp tèc ®é:
Z = p1.p2…pi
pi: sè tû sè truyÒn nhãm truyÒn thø i.
Çc çch thùc hiÖn çc trÞ sè pi kh¸c nhau vµ ho¸n
vÞ chóng cho çc ph-¬ng ¸n kh«ng gian kh¸c nhau.
HT§
Cã nhiÒu nhãm truyÒn

21
 Pi lµ c¸c sè nguyªn. Chän pi = 2 hoÆc 3 lµ ph-¬ng
¸n tèi -u nhÊt.
 §èi víi mét tæng sè cÊp tèc ®é cã nhiÒu ph-¬ng
¸n kh«ng gian.
VÝ dô:
XÐt mét HT§ cã Z = 12.
LËp c¸c ph-¬ng ¸n kh«ng gian cã thÓ:
Z = 3 x 2 x 2
= 2 x 3 x 2
= 2 x 2 x 3

22
•Ph-¬ng ¸n 3 x 2 x 2
Nhãm 1
p1 = 3
Nhãm 2
p2 = 2
Nhãm 3
p3 = 2
n1 – n12

23
•Ph-¬ng ¸n 2 x 3 x 2 •Ph-¬ng ¸n 2 x 2 x 3

24
 Víi Z = 18 cã çc ph-¬ng ¸n kh«ng gian:
Z = 3 x 3 x 2 = 3 x 2 x 3 = 2 x 3 x 3
 Víi Z = 24 cã çc ph-¬ng ¸n:
Z = 3 x 2 x 2 x 2 = 2 x 3 x 2 x 2 = 2 x 2 x 3 x 2
= 2 x 2 x 2 x 3.
(Ph-¬ng ¸n Z= 2 x 3 x 2 x 2 dïng cho m¸y T620)
 So s¸nh çc ph-¬ng ¸n kh«ng gian: b»ng çc tÝnh
to¸n s¬ bé:
 Th-êng nh÷ng nhãm truyÒn cã nhiÒu tst ®-îc ®Æt
lªn tr-íc sÏ cho kÝch th-íc nhá gän h¬n (v× trôc I
cã tèc ®é quay lín  m«men xo¾n nhá  kÝch
th-íc nhá)

25
 Tæng sè trôc: Str= i+1
 Tæng sè b¸nh r¨ng: Sr= 2(p1.p2....pi)
 Th-êng chän s¬ bé chiÒu réng b¸nh r¨ng b»ng
nhau vµ b»ng b
 ChiÒu dµi tèi thiÓu çc khèi BR:
L2bËc = 4b + 2f vµ L3bËc = 7b + 4f
Chó ý: ë ®©y kh«ng
kÓ ®Õn kho¶ng çch
gi÷a çc b¸nh r¨ng

26
LËp b¶ng so s¸nh c¸c ph-¬ng ¸n kh«ng gian:
PAKG
ChØ tiªu
3 x 2 x 2 2 x 3 x 2 2 x 2 x 3
Tæng sè BR 14 14 14
Tæng sè trôc 4 4 4
ChiÒu dµi trôc
Lmin
15b + 8f 15b + 8f 15b + 8f
Sè BR chÞu
M«men xo¾n lín
2 2 3
C¬ cÊu ®Æc biÖt
Lùa chän mét ph-¬ng ¸n kh«ng gian hîp lý

27
2.2.1 Ph-¬ng ¸n thø tù (PA thay ®æi)
 Thay ®æi thø tù ¨n khíp cña çc BR theo thø
tù nhãm, ta sÏ ph©n tÝch kÕt qu¶ cña sù thay
®æi ®ã ®Ó t×m quy luËt ph©n bè chuçi tû sè
truyÒn u trong tõng nhãm truyÒn.
VÝ dô:
Z = 12, PAKG: 3 x 2 x 2
- Nhãm 1 gåm çc tû sè truyÒn: u1, u2, u3
- Nhãm 2 gåm çc tû sè truyÒn: u4, u5
- Nhãm 3 gåm çc tû sè truyÒn: u6, u7
 TrÞ sè vßng quay trôc chÝnh:

28
 G¹t: nhãm 1 – nhãm 2 – nhãm 3:
 G¹t: Nhãm 3 – nhãm 2 – nhãm 1:
n1 = n0.u1.u4.u6
n2 = n0.u2.u4.u6
n3 = n0.u3.u4.u6
n4 = n0.u1.u5.u6
n5 = n0.u2.u5.u6
n6 = n0.u3.u5.u6
n7 = n0.u1.u4.u7
n8 = n0.u2.u4.u7
n9 = n0.u3.u4.u7
n10 = n0.u1.u5.u7
n11 = n0.u2.u5.u7
n12 = n0.u3.u5.u7
n1 = n0.u1.u4.u6
n2 = n0.u1.u4.u7
n3 = n0.u1.u5.u6
n4 = n0.u1.u5.u7
n5 = n0.u2.u4.u6
n6 = n0.u2.u4.u7
n7 = n0.u2.u5.u6
n8 = n0.u2.u5.u7
n9 = n0.u3.u4.u6
n10 = n0.u3.u4.u7
n11 = n0.u3.u5.u6
n12 = n0.u3.u5.u7
 T×m quan hÖ cña tõng nhãm
(l-u ý: n1 n12 lµ cÊp sè nh©n c«ng béi )

29
PATT: I – II – III
 Nhãm 1: u1:u2:u3 = n1:n2:n3
mµ n1:n2:n3 = n1:n1:n12 = 1::2 - lµ cÊp sè
nh©n, c«ng béi X víi X = 1.
 Nhãm 2: u4:u5 = n1:n4 = 1:3; u4, u5 lµ cÊp sè
nh©n, c«ng béi víi X1 = 3 = p1.
 Nhãm 3: u6:u7 = n1:n7 = 1: 6; u6, u7 lµ cÊp sè
nh©n, c«ng béi víi X2 = 6 = 3.2 =p1 p2
 Gäi nhãm thay ®æi 1 lµ nhãm c¬ së, c¸c tû sè
truyÒn lµ cÊp sè nh©n X víi X = 1
1X

2X


30
 Nhãm thay ®æi 2 lµ nhãm khuÕch ®¹i 1, c¸c tû
sè truyÒn lµ cÊp sè nh©n, c«ng béi víi X1
= p1 – lµ sè tû sè truyÒn nhãm c¬ së.
 Nhãm thay ®æi 3 lµ nhãm khuÕch ®¹i 2, c¸c tû
sè truyÒn lµ cÊp sè nh©n, c«ng béi víi
X2 = p1p2, p2 – lµ sè tû sè truyÒn nhãm K§1
 Tõ 1 PAKG, cã nhiÒu PATT
 Sè PATT = (Sè nhãm truyÒn)!
VÝ dô:
cã 3 nhãm truyÒn
 Sè PATT lµ 3! = 3.2.1 = 6
1X

2X


31
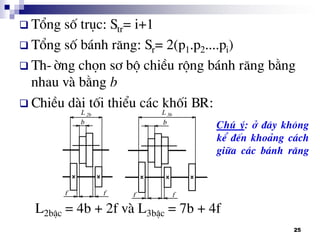
PAKG 3 x 2 x 2
PATT I II III
§Æc tÝnh nhãm: [1] [3] [6]
3[1] 2[3] 2[6]
PAKG 3 x 2 x 2
PATT III II I
§Æc tÝnh nhãm: [4] [2] [1]
3[4] 2[2] 2[1]
PAKG 3 x 2 x 2
PATT I III II
§Æc tÝnh nhãm: [1] [6] [3]
3[1] 2[6] 2[3]
PAKG 3 x 2 x 2
PATT II I III
§Æc tÝnh nhãm: [2] [1] [6]
3[2] 2[1] 2[6]
PAKG 3 x 2 x 2
PATT III I II
§Æc tÝnh nhãm: [4] [1] [2]
3[4] 2[1] 2[2]
PAKG 3 x 2 x 2
PATT II III I
§Æc tÝnh nhãm: [2] [6] [1]
3[2] 2[6] 2[1]

32
2.2.3 L-íi kÕt cÊu
 S¬ ®å biÓu diÔn c«ng thøc kÕt cÊu vµ ph-¬ng
tr×nh ®iÒu khiÓn
 Mçi ®-êng th¼ng ngang biÓu diÔn 1 trôc HT§
 Sè ®-êng th¼ng th¼ng ®øng biÓu diÔn sè cÊp
tèc ®é
 BiÓu diÔn chuçi n t¨ng theo cÊp sè nh©n, ta vÏ
l-íi kÕt cÊu theo täa ®é logarit vµ ®èi xøng.
(Ta cã: n2 = n1  lgn2 = lgn1+lg
u4:u5 = 1:3  lgu5 = lgu4+3lg)

33
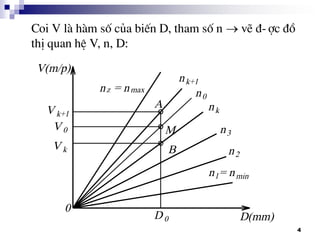
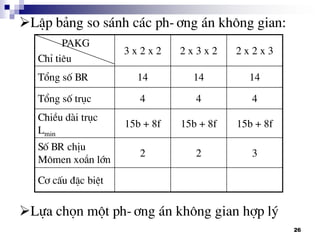
 VÝ dô: vÏ l-íi kÕt cÊu cho HT§ cã:
PAKG 3 x 2 x 2
PATT I II III
§Æc tÝnh nhãm: [1] [3] [6]
- Tèc ®é trªn trôc II: nII
1 = n0.u1
nII
2 = n0.u2
nII
3 = n0.u3
u1u2u3
u4u5
III
n0 I
u6u7
IV
n1  n12
II
Trªn trôc III:
nIII = nII. u4
nII. u5
…

34
Theo quy -íc vÏ ®èi xøng  n0 n»m chÝnh gi÷a trôc I.
VÏ 3 tia ®Æc tr-ng cho 3 tû sè truyÒn u1, u2, u3 theo çc
quy -íc ë trªn. XÐt çc tèc ®é trªn trôc II:
nII
1: nII
2: nII
3 = u1: u2: u3 = 1::2  lg nII
3 - lg nII
2 =
lg nII
2 - lg nII
1 = lg. Çc trôc kh¸c lµm t-¬ng tù.

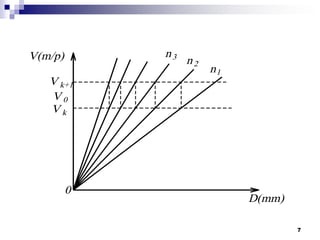
35
 NÕu chän PATT kh¸c sÏ cã sù ph©n bè tèc ®é
trung gian kh¸c nhau:
3 x 2 x 2
III II I
[4] [2] [1]
 Mçi PATT cã mét l-íi kÕt cÊu

36
 C¸c kh¸i niÖm:
 L-îng më l©n cËn
 L-îng më lín nhÊt
Chän l-íi kÕt cÊu cÇn ®¶m b¶o: l-îng më, tû sè truyÒn
cña c¸c nhãm thay ®æi tõ tõ, ®Òu ®Æn, trong giíi h¹n cho
phÐp. PA h×nh rÎ qu¹t cho kÝch th-íc hép nhá gän.
3 x 2 x 2
II III I
[2] [6] [1]

37
B¶ng so s¸nh c¸c PATT
Nh-îc ®iÓm cña l-íi kÕt cÊu: kh«ng biÓu diÔn ®-îc tû
sè truyÒn cô thÓ, c¸c trÞ sè vßng quay cô thÓ, nªn kh«ng
tÝnh ®-îc truyÒn dÉn cho hép.

38
2.2.4 §å thÞ vßng quay:
 BiÓu diÔn çc tû sè truyÒn, çc sè vßng quay cô
thÓ
 Quy -íc:
Chó ý: Çc tû sè truyÒn cã sè mò b»ng ®é nghiªng
cña tia (nghiªng mÊy «?)

39
 Kh«ng cÇn vÏ ®èi xøng
 §¶m b¶o l-îng më l©n cËn
 Nªn chän tèc ®é n0 vÒ phÝa tèc ®é cao
 Nguyªn t¾c chän tû sè truyÒn:
 Gi¶m ®Òu tõ trôc ®Çu tiªn  trôc cuèi cïng
 Giíi h¹n tû sè truyÒn: 1/4  u  2  Xmax  8
(Xmax = umax/umin = 8)
 Sao cho sè vßng quay trôc trung gian cµng cao cµng
tèt.

40
 VÉn vÝ dô trªn: ta chän tû sè truyÒn cho:
 Nhãm c¬ së: chän u1 = 1/ 2  u2 = 1/ , u3 = 1
(v× u1:u2:u3 = 1: : 2)
 Nhãm K§1: u4 = 1/ 2; u5 = 
 Nhãm K§2: u6 = 1/ 4; u7 = 2. Ta cã §TVQ:

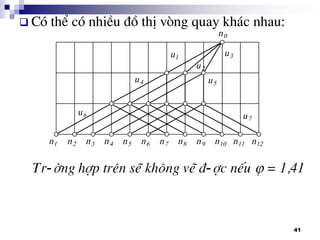
41
 Cã thÓ cã nhiÒu ®å thÞ vßng quay kh¸c nhau:
Tr-êng hîp trªn sÏ kh«ng vÏ ®-îc nÕu  = 1,41

42
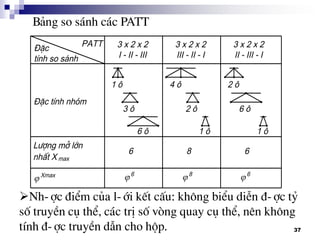
 Tr-êng hîp ®èi víi m¸y tiÖn T620 cã Z = 24
(thùc tÕ lµ 23), ng-êi ta chän PAKG:
Z = 2 x 3 x 2 x 2 (Nhãm 1 dïng 2 tû sè truyÒn
®Ó cã thÓ chøa bé ly hîp ma s¸t ®Üa trªn trôc
thø nhÊt).
Vµ PA dïng lµ: 2 x 3 x 2 x 2
I – II – III – IV
[1] [2] [6] [12]
L-îng më lín nhÊt Xmax = 12, v-ît qu¸ gi¸ trÞ
cho phÐp
(v× HT§ nµy cã
Xmax = 1,2612 =16 > 8)
259,1
5,12
2000
123  

43
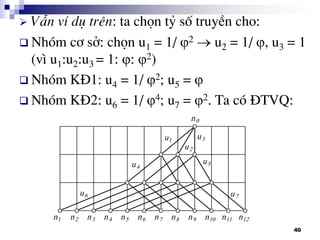
 Gi¶i ph¸p: - Thu hÑp l-îng më  trïng tèc ®é, ph¶i
t×m c¸ch bï tèc ®é
- Thªm trôc trung gian
XÐt h×nh vÏ:
Víi  = 1,26  u = 1/9:
v-ît qu¸ giíi h¹n cho phÐp
 Thªm trôc trung gian,
t¸ch thµnh 2 tû sè truyÒn:
u = 1/3 vµ u = 1/6
9
1

3 3
1 1 1
1,26 2
 
6 6
1 1 1
1,26 4
 
• L-íi kÕ cÊu cña PA 2 x 3 x 2 x 2
I – II – III – IV
[1] [2] [6] [12]
Sau khi thu hÑp l-îng më Xmax = 12  Xmax = 6:

44
 cã 6 tèc ®é bÞ trïng  bï 6 tèc ®é b»ng c¸ch ghÐp
thªm 1 HT§ míi (thùc chÊt thªm 1 cÆp BR u11)
PAKG biÕn h×nh cña T620: Z = Z1 + Z2
Z1 = 2 x 3 x 2 x 2 x 1
Z2 = 2 x 3 x 1
Z = (2 x 3) x [(2 x 2 x 1)+1]

45
 Z1 = 2 x 3 x 2 x 2 x 1
[1] [2] [6] [12] [0]
[6]
Z2 = 2 x 3 x 1
[1] [2] [0]

46
 Sè cÊp tèc ®é thùc tÕ cßn: (24 - 6) + (6 – 1) = 23
 ViÖc ®Ó trïng tèc ®é n18 = 630 vg/ph lµ do chñ ý cña
ng-êi thiÕt kÕ, v× hoµn toµn cã thÓ t¹o ®-îc c¶ 24
tèc ®é khi chän u11 = 3 = 2 (®-êng nÐt ®øt), thùc tÕ
kh«ng dïng víi môc ®Ých tr¸nh ån
 Thùc tÕ cßn tuú theo yªu cÇu tèc ®é cao víi ®iÒu
kiÖn kÕt cÊu vµ c«ng nghÖ nªn gi÷a hai ®-êng
truyÒn dÉn cã thÓ bè trÝ trïng tèc ®é. M¸y 16K20 cã
22 tèc ®é, do trïng 2 tèc ®é:
Z1 = 2 x 3 x 2 x 1 x 1
[1] [2] [6] [0] [0]
Z2 = 2 x 3 x 2
[1] [2] [6] [4]
 Còng cã thÓ tr¸nh trïng tèc ®é b»ng c¸ch kh«ng
thu hÑp l-îng më cña ®-êng truyÒn thø 2, tøc u11 =
3 = 2

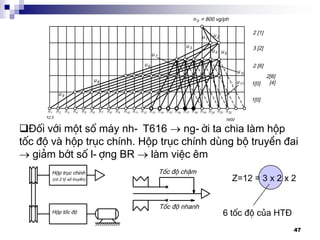
47
§èi víi mét sè m¸y nh- T616  ng-êi ta chia lµm hép
tèc ®é vµ hép trôc chÝnh. Hép trôc chÝnh dïng bé truyÒn ®ai
 gi¶m bít sè l-îng BR  lµm viÖc ªm
Z=12 = 3 x 2 x 2
6 tèc ®é cña HT§

48
 §èi víi m¸y 1A616, cã Z = 24 = 3 x 4 x 2
HT§ HTC
 HT§: Z1 + Z2 = 3 x 4 = (2 x 4 x 1) +(1 x 4 x 1)
Z1 = 2 x 4 x 1 x 2
[1] [2] [0] [8]
Z2 = 1 x 4 x 1 x 2
[0] [2] [0] [8]
( = 1,26)

49
  Cã 24 tèc ®é, trïng 3  cßn l¹i 21 tèc ®é
 Më réng l-îng më Xmax = 8 lªn Xmax = 9  uk®
 Chuçi sè c¸ch qu·ng ë tèc ®é thÊp
 Do chØ cã 1 ®c¬ nªn kh«ng t¹o ra n01, mµ dïng
chung n02  l-îng më v-ît qu¸ giíi h¹n, 
gi¶m n02  n0

50
2.2.5 TÝnh sè r¨ng cña çc BR trong mét nhãm truyÒn:
 Khi ®· biÕt ®-îc çc tû sè truyÒn trong nhãm  cÇn t×m
sè r¨ng cho çc BR Z1, Z1
’, Z2, Z2
’,… Cã 2 TH x¶y ra:
 BiÕt tr-íc kho¶ng çch trôc A: vÝ dô nh- ®· cã s½n mét
vá m¸y,…  tÝnh sè r¨ng:
 Ch-a biÕt kho¶ng çch trôc A: x¸c ®Þnh sè r¨ng theo
ph-¬ng ph¸p BSCNN:
• Çc BR n»m trªn 2 trôc song song
• BiÕt tr-íc çc tû sè truyÒn, nh- u = 1, u = 1/x, u = x
• Rót gän thµnh çc ph©n sè tèi gi¶n
 
'2
;
1
x x x x
x
A
Z Z u Z
m u
 


51
1
1
1
;
f
u
g
 2
2
2
;
f
u
g
 3
3
3
;...
f
u
g
 x
x
x
f
u
g

NÕu cïng m«®un, ta cã:
' ' '
1 1 2 2 ... x xZ Z Z Z Z Z Z       
MÆt kh¸c:
1
1
1
;
f
u
g
 2
2
2
;
f
u
g
 3
3
3
;...
f
u
g
 x
x
x
f
u
g

'
x x
x
x
x
Z Z Z
f
u
g
  

Lµ hÖ 2 pt, 3 Èn sè
Gi¶ sö biÕt ®-îc Z '
. ; .x x
x x
x x x x
f g
Z Z Z Z
f g f g
    
 

52
Zx vµ Zx
’ ph¶i lµ çc sè nguyªn Z.fx vµ Z.gx
ph¶i chia hÕt cho (fx + gx). Do fx/gx ®· tèi gi¶n Z
ph¶i chia hÕt cho (fx + gx):
Tøc lµ: Z = EK, trong ®ã K: BSCNN cña çc (fx+gx)
Trong ®ã E lµ sè nguyªn, E  Emin, ®Ó sè r¨ng nhá
nhÊt  Zmin = 17
-Khi BR nhá nhÊt lµm chñ ®éng:  
min
17
.
x x
x
f g
E
f K


Chñ
-Khi BR nhá nhÊt lµm bÞ ®éng:
 
min
17
.
x x
x
f g
E
g K


BÞ
• Tr-êng hîp çc cÆp BR cã Z kh¸c nhau  dïng
m«®un kh¸c nhau
• Còng cè thÓ dïng BR dÞch chØnh víi Z =  3

53
• TÝnh sè r¨ng c¸c BR cho tõng nhãm
• Th«ng th-êng Z1 < Z2 < Z3 vµ Z  120
•Tr-êng hîp víi (fx+gx) >120 (kh«ng tèi
gi¶n ®-îc n÷a)  chän sao cho:
x
x
x
f
u
g

'
'
x
x
x
f
u
g
' '
120x xf g  chÞu sai sè tèc ®é, víi  [ ] 10 1 %n    
VÝ dô tæng hîp:
ThiÕt kÕ ®éng häc HT§ cã Z = 8, nmin = 160 vg/ph;
= 1,26.
1.X¸c ®Þnh chuçi sè vßng quay tiªu chuÈn:

54
n1 = nmin = 160
n2 = 200
n3 = 250
n4 = 315
n5 = 400
n6 = 500
n7 = 630
n8 = 800
2. Chän ph-¬ng ¸n kh«ng gian:
Z = 2 x 2 x 2
3. Chän ph-¬ng ¸n thø tù: I – II – III
[1] [2] [4]

55
4. L-íi kÕt cÊu vµ ®å thÞ vßng quay:
NÕu chän ®å thÞ vßng quay nh- ph-¬ng ¸n a) trªn
h×nh vÏ  sè vßng quay trôc trung gian ch-a cao
vµ tèc ®é t¨ng tèc vµ gi¶m tèc ë trôc cuèi cïng cã
l-îng më nh- nhau.
Do ®ã chän ph-¬ng ¸n b

56
5. TÝnh sè r¨ng c¸c b¸nh r¨ng:
Do ®· chän tû sè truyÒn cho c¸c nhãm (thÓ hiÖn
trªn §TVQ):
1
1
1;
5
4
125
100
25,1
1
26,1
11
21  uu

3 42 2
1 1 1 1 10 5 1
; 1
1,26 1,58 1,6 16 8 1
u u

       
5 63 3
1 1 1 5
; 1,26
1,26 2 4
u u 

     
• Nhãm I: f1 + g1 = 4 + 5 = 9
f2 + g2 = 1 + 1 = 2
K = 18
 
min 1
17. 4 5
3 Z 3.18 54
4.18
E

     

57
• Nhãm II: f3 + g3 = 5 + 8 = 13
f4 + g4 = 1 + 1 = 2
K = 26
 
min 2
17. 5 8
2 Z 2.26 52
5.26
E

     
• Nhãm III: f5 + g5 = 1 + 2 = 3
f6 + g6 = 5 + 4 = 9
K = 9
 
min 3
17. 1 2
6 Z 6.9 54
1.9
E

     
• Tõ ®ã t×m ®-îc:
 
'
1 1
4.54
24 30
4 5
Z Z   

• C¸c cÆp kh¸c t×m t-¬ng tù. KÕt qu¶:
3 5 61 2 4
' ' ' ' ' '
1 2 3 4 5 6
24 27 20 26 18 30
; ; ; ; ;
30 27 32 26 36 24
Z Z ZZ Z Z
Z Z Z Z Z Z
     

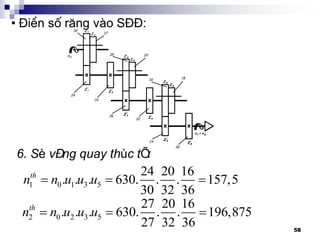
58
• §iÒn sè r¨ng vµo S§§:
6. Sè vßng quay thùc tÕ:
1 0 1 3 5
24 20 16
. . . 630. . . 157,5
30 32 36
th
n n u u u  
2 0 2 3 5
27 20 16
. . . 630. . . 196,875
27 32 36
th
n n u u u  

59
3 0 1 4 5
24 26 16
. . . 630. . . 252
30 26 36
th
n n u u u  
4 0 2 4 5
27 26 16
. . . 630. . . 315
27 26 36
th
n n u u u  
5 0 1 3 6
24 20 30
. . . 630. . . 400
30 32 24
th
n n u u u  
6 0 2 3 6
27 20 30
. . . 630. . . 500
27 32 24
th
n n u u u  
7 0 1 4 6
24 26 30
. . . 630. . . 630
30 26 24
th
n n u u u  
8 0 2 4 6
27 26 30
. . . 630. . . 800
27 26 24
th
n n u u u  

60
 Sai sè sè vßng quay:
.100%
tc th
i i
i tc
i
n n
n
n

 
1
160 157,5
.100% 1,56%
160
n

  
Víi [n] = 10( - 1)%
T-¬ng tù:
n2 = 1,56%; n3 = - 0,8%; n4 = 0;
n5 = 1,56%; n6 = 1,56%; n7 = 0
n8 = 1,56%
 BiÓu diÔn sai sè:

61
2.3 Hép tèc ®é dïng ®éng c¬ nhiÒu tèc ®é:
Th«ng th-êng:
720/1440/2880 (3 tèc ®é)
1440/2880 (2 tèc ®é)
Ph¶i coi ®éng c¬ lµ mét nhãm truyÒn
2 tèc ®é   = 2
(X  1)
3 tèc ®é   = 2
(X  1)

62
 MÆc dï lµ nhãm ®Çu, nh-ng kh«ng thÓ chän nã lµm
nhãm c¬ së (X víi X = 1)
 §éng c¬ cã Z = 12 = 2 x 3 x 2, cã thÓ dïng víi
 =1,26 hoÆc  = 1,41
-  = 1,41 th× PA duy nhÊt lµ:
-  = 1,26 th× sö dông ®-îc PA:
2 x 3 x 2
II III I
[2] [4] [1]
2 x 3 x 2
II I III
[3] [1] [6]

63
3.1 §Æc ®iÓm vµ c¸c yªu cÇu chung vÒ HCD
3.1.1 §Æc ®iÓm:
 C«ng suÊt truyÒn dÉn bÐ: 5  10% c«ng suÊt chÝnh
 Tèc ®é quay chËm
  HCD cho phÐp dïng c¸c bé truyÒn hiÖu suÊt
thÊp: + Trôc vÝt – b¸nh vÝt
+ VÝt me – ®ai èc
- L-íi kÕt cÊu kh«ng cÇn dïng PA h×nh rÎ qu¹t
- Kh«ng nhÊt thiÕt chän nhãm I lµm nhãm c¬ së
- Giíi h¹n tû sè truyÒn: 1/5  u  2,8
3.1.2 Yªu cÇu:
 §¶m b¶o giíi h¹n l-îng ch¹y dao Smin  Smax
 §¶m b¶o sè l-îng ch¹y dao ZS
3. ThiÕt kÕ truyÒn dÉn hép ch¹y dao

64
 §¶m b¶o quy luËt ph©n bè l-îng ch¹y dao (th«ng
th-êng lµ cÊp sè nh©n, khi tiÖn ren th× võa theo
cÊp sè nh©n, võa theo cÊp sè céng)
 TÝnh chÊt c¸c l-îng ch¹y dao (liªn tôc/gi¸n ®o¹n)
 §é chÝnh x¸c tû sè truyÒn (vÝ dô ë m¸y tiÖn: liªn
quan ®Õn ®é chÝnh x¸c b-íc ren)
 §¶m b¶o ®é cøng v÷ng cña xÝch truyÒn (kh«ng
dïng ly hîp an toµn, ly hîp siªu viÖt)
3.1.3 C¸c lo¹i hép ch¹y dao: chia HCD lµm 3 nhãm:
1. Hép ch¹y dao th«ng th-êng, ®¶m b¶o cho dao
hoÆc ph«i cã ®-îc 1 tèc ®é di chuyÓn cÇn thiÕt
trong qu¸ tr×nh c¾t (m¸y phay, khoan, doa,…)

65
L-îng ch¹y dao ph©n bè theo quy luËt cÊp sè nh©n
 gièng nh- HT§  cho phÐp sai sè vÒ l-îng ch¹y
dao S  thiÕt kÕ gièng HT§ (chän PAKG, PATT,
LKC, §TVQ, sè r¨ng, tÝnh S).
Chó ý: L-íi kÕt cÊu kh«ng cÇn dïng PA h×nh rÎ qu¹t
2. Hép ch¹y dao t¹o chuyÓn ®éng kh«ng liªn tôc (gi¸n
®o¹n) dïng trong c¸c m¸y bµo, xäc.
3. Hép ch¹y dao ®¶m b¶o tû sè truyÒn chÝnh x¸c (gi÷a
trôc chÝnh vµ ph«i):
- HCD tiÖn ren
- HCD t¹o ra chuyÓn ®éng bao h×nh (1 vßng dao 
K/Z vßng ph«i)

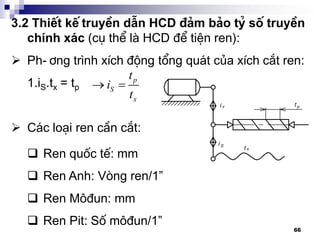
66
3.2 ThiÕt kÕ truyÒn dÉn HCD ®¶m b¶o tû sè truyÒn
chÝnh x¸c (cô thÓ lµ HCD ®Ó tiÖn ren):
 Ph-¬ng tr×nh xÝch ®éng tæng qu¸t cña xÝch c¾t ren:
1.iS.tx = tp
 C¸c lo¹i ren cÇn c¾t:
p
S
x
t
i
t
 
 Ren quèc tÕ: mm
 Ren Anh: Vßng ren/1”
 Ren M«®un: mm
 Ren Pit: Sè m«®un/1”

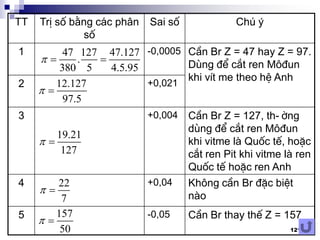
67
 NÕu b-íc vitme lµ mm vµ c¸c b-íc ren cÇn c¾t:
 Quèc tÕ: tp (mm)
 M«®un: m (mm)
 Anh: 25,4/n (mm)
 Pit: 25,4./Dp (mm)
(Dp - §-êng kÝnh pÝt, ®o b»ng sè r¨ng trªn 1 ®v ®-êng kÝnh
cña Br tÝnh b»ng Inch)
 §Ó kh«ng cã sai sè: ren cÇn c¾t vµ tx ph¶i cã cïng
mét ®¬n vÞ.  M¸y v¹n n¨ng chØ cã mét lo¹i ren
®-îc c¾t ®óng, 3 lo¹i cßn l¹i cã sai sè, nhiÖm vô lµ
ph¶i ®¶m b¶o sai sè b-íc ren < [sai sè b-íc ren]
(sai sè ‰ hoÆc ‰0)  ®¶m b¶o sai sè tÝch luü
Kh«ng cã sai sè`
Do lÎ  cã sai sè`

68
 C¸c b-íc thiÕt kÕ:
 S¾p xÕp b-íc ren thµnh hµng, cét t¹o nhãm c¬ së
vµ nhãm gÊp béi
 ThiÕt kÕ truyÒn dÉn nhãm c¬ së
 ThiÕt kÕ truyÒn dÉn nhãm gÊp béi
 TÝnh ibï, tÝnh sai sè b-íc ren
 TÝnh søc bÒn c¸c chi tiÕt trong hép ch¹y dao
 Ph-¬ng tr×nh c¾t ren tæng qu¸t:
1.ic®.iS.tx = tp
§Ó chän b-íc ren cÇn c¾t lµ Quèc tÕ, Anh, …, b-íc
ren tr¸i, ph¶i, … ta cã ph-¬ng tr×nh cô thÓ sau:

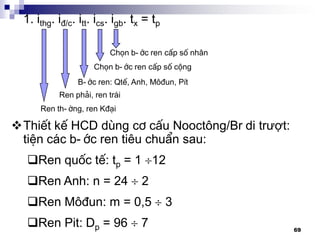
69
1. ithg. i®/c. itt. ics. igb. tx = tp
Ren th-êng, ren K®¹i
Ren ph¶i, ren tr¸i
B-íc ren: QtÕ, Anh, M«®un, PÝt
Chän b-íc ren cÊp sè céng
Chän b-íc ren cÊp sè nh©n
ThiÕt kÕ HCD dïng c¬ cÊu Nooct«ng/Br di trượt:
tiÖn c¸c b-íc ren tiªu chuÈn sau:
Ren quèc tÕ: tp = 1 12
Ren Anh: n = 24  2
Ren M«®un: m = 0,5  3
Ren Pit: Dp = 96  7

70
12631,5
115,5--
1052,51,25
94,52,25-
8421
73,51,75-
a.S¾p xÕp b-íc ren: (kh«ng trïng, thiÕu tèc ®é)
1,75
2,00
2,25
2,50
-
3
-
1
-
1,25
-
1,5
-
0,5
-
-
-
-
-
-
-
-
-
-
CÊp sè nh©n (nhãm gÊp béi)
CÊpsècéng(nhãmc¬së)
Ren Quèc tÕ Ren M«®un

71
-
14
16
18
20
22
24
-
-
28
32
36
40
44
48
-
-
56
64
72
80
88
96
-
-
7
8
9
10
11
12
-
3¼
3½
4
4½
-
5
-
6
-
7
8
9
(9,5)
10
11
12
13
14
16
18
19
20
(22)
24
-
-
2
-
-
-
-
3
Ren Anh Ren PÝt
Sè r¨ng cña bé Nooct«ng tû lÖ víi n(khi c¾t ren Anh),
víi Dp (khi c¾t ren Pitch), víi tp (khi c¾t ren Quèc tÕ),
víi m (khi c¾t ren M«®un).
§Ó tr¸nh kÐm cøng v÷ng, sè Br cña bé Nooct«ng
ph¶i < 10  13 b¸nh

72
b.ThiÕt kÕ nhãm c¬ së:
 Dùng cơ cấu Nooctông:
Z1, Z2,… lµ sè r¨ng cña bé Nooct«ng, ta cã:
- Khi c¾t ren Quèc tÕ:
Z1:Z2:Z3:Z4:Z5:Z6 = 7:8:9:10:11:12
Chó ý: ®Ó kÝch th-íc nhãm truyÒn kh«ng qu¸ lín,
ng-êi ta h¹n chÕ 25 < Zi < 60
 Chän: Z1:Z2:Z3:Z4:Z5:Z6 = 28:32:26:40:44:48
- Khi c¾t ren m«®un:
Z1:Z2:Z3:Z4:Z5 = 1,75:2:2,25:2,5:3
 Chän: Z1:Z2:Z3:Z4:Z5 = 28:32:36:40:48

73
- Khi c¾t ren Anh:
Z1:Z2:Z3:Z4:Z5:Z6:Z7:Z8 = 13:14:16:18:19:20:22:24
 Chän:
Z1:Z2:Z3:Z4:Z5:Z6:Z7:Z8 = 26:28:32:36:38:40:44:48
- Khi c¾t ren Pit:
Z1:Z2:Z3:Z4:Z5:Z6 = 56:64:72:80:88:96
 Chän: Z1:Z2:Z3:Z4:Z5:Z6 = 28:32:36:40:44:48
§Ó c¾t ®-îc c¶ 4 lo¹i ren trªn, bé Nooct«ng ph¶i cã
c¸c Br:
Zn = 26,28,32,36,38,40,44,48

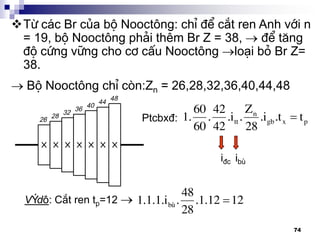
74
Tõ c¸c Br cña bé Nooct«ng: chØ ®Ó c¾t ren Anh víi n
= 19, bé Nooct«ng ph¶i thªm Br Z = 38,  ®Ó t¨ng
®é cøng v÷ng cho c¬ cÊu Nooct«ng lo¹i bá Br Z=
38.
 Bé Nooct«ng chØ cßn:Zn = 26,28,32,36,40,44,48
Ptcbx®:
n
tt gb x p
Z60 42
1. . .i . .i .t t
60 42 28

i®c ibï
VÝ dô: C¾t ren tp=12  bï
48
1.1.1.i . .1.12 12
28


75
Dùng bánh răng di trượt:
211/21/4
1473,51,75
12631,5
115,52,75-
1052,51,25
94,52,25-
8421
Ren quốc tế: tp = 1  14
Viết lại pt cắt ren:
1.ithg. iđc. itt. ics. igb. tx = tp
Chän nhãm tp = 4; 4,5; 5; 5,5, 6;
7 lµm nhãm c¬ së
 ithg = 1, iđc = 1, igb = 1, bước vit
me tx và itt chọn trước theo máy
tham khảo
Ví dụ: máy 1A616, tx = 6 mm
Chọn itt = 30/36     
p
cs p cs p
t30 36 1
1.1.1. .i .1.6 t i . t
36 6 30 5
 cs
4 9 5 11 6 7
i ; ; ; ; ;
5 10 5 10 5 5

76
Chó ý:
- §Ó gi¶m Sè Br di tr-ît  dïng ph-¬ng ph¸p dÞch
chØnh r¨ng
- Dïng nhiÒu lo¹i M«®un kh¸c nhau
- ChÊp nhËn Z =  3
- Dùa vµo m¸y cò chän kho¶ng çch trôc thuéc nhãm
c¬ së
- VÝ dô dùa vµo m¸y 1A616, kho¶ng çch t©m
A=78mm
 Víi çc gi¸ trÞ cña m kh¸c nhau  Z kh¸c nhau.
D-íi ®©y lµ b¶ng tÝnh sè r¨ng cña nhãm c¬ së.
2A
Z
m
  

77
Tû sè truyÒn nhãm c¬ së cs
A
i
B

4
5
9
10
1
1
11
10
6
5
7
5
36
40
39
39
42
35
32
40
42
30
31
31
33
30
35
25
27
30
29
29
35
25
24
30
27
27
30
25
20
25
21
21
22
20
24
20
18
20
20
20
----439
--3,543
---354
---2,7558
---2,5063
---2,2570
--278
1211212199Z
-
35
35
gx+fx
m

78
- Sau khi ®· cã b¶ng nµy  chọn các cặp ô cùng
hàng ngang liền nhau có cùng tử (hoặc mẫu)  ghép
thành một đôi (có 3 Br) tạo ra 3 tst
- C¸c « lÎ  kh«ng ¨n khíp chung.
- Tr-êng hîp sau khi tÝnh to¸n kh«ng cã Br dïng
chung nµo  chän l¹i A, itt, tx,… mét lo¹t ics míi, lÆp
l¹i qu¸ tr×nh.
Nhãm c¬ së dïng Br di tr-ît, cã 2 Br chung

79
11/21/41/8
211/21/4
12631,5
115,5--
1052,51,25
94,52,25-
8421
73,51,75-
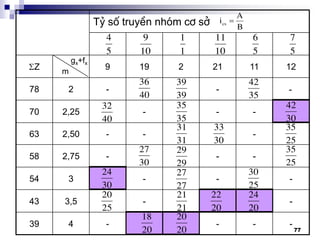
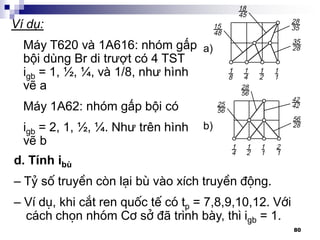
c. Thiết kế nhóm gấp bội:
Nhóm gấp bội phải tạo ra
4 TST, công bội  = 2
Trị số phụ thuộc vào việc
chọn cột nào làm nhóm cơ
sở
Nhóm gấp bội dùng Br
răng di trượt được thiết kế
giống như HTĐ đã trình
bày:
Z = 4 = 2 x 2
I II
[1] [2]

80
Ví dụ:
Máy T620 và 1A616: nhóm gấp
bội dùng Br di trượt có 4 TST
igb = 1, ½, ¼, và 1/8, như hình
vẽ a
Máy 1A62: nhóm gấp bội có
igb = 2, 1, ½, ¼. Như trên hình
vẽ b
a)
b)
d. TÝnh ibï
– Tû sè truyÒn cßn l¹i bï vµo xÝch truyÒn ®éng.
– VÝ dô, khi c¾t ren quèc tÕ cã tp = 7,8,9,10,12. Víi
c¸ch chän nhãm C¬ së ®· tr×nh bµy, th× igb = 1.

81
n
tt gb x p
Z60 42
1. . .i . .i .t t
60 42 28

i®c ibï
Ptc®: (dïng c¬ cÊu Nooctong)
Gi¶ sö c¾t tp = 12, lóc nµy Zn = 48. B-íc vÝt me tx = 12.
Ta cã:
bï
48
1.1.1.i . .1.12 12
28
  bï
12 28 7
i .
12 48 12
ibï = ic®.itt, chän tr-íc itt = 42/50  bï c®
42
i .i
50
 c®
25
i
36
Chó ý: Khi c¾t ren quèc tÕ vµ m«®un, khèi Nooctong
chñ ®éng, khi c¾t ren Anh vµ Pit th× khèi Nooctong lµ bÞ
®éng

82
Cïng víi itt ®ã  dïng ®Ó c¾t ren Anh, víi ®-êng
truyÒn kh¸c.
 n
cs
Z 25
NÕu coi i .
36 28
igb
thì 
cs n
1 28 36
.
i 25 Z
Ptxđ khi cắt ren Anh: gb x
n
60 42 42 28 36 25,4
1. . . . . .i .t
60 42 50 25 Z n

83
Ren Pit vµ ren Anh ®Òu dïng chung mét ®-êng truyÒn,
víi itt kh¸c nhau.
TÝnh sai sè b-íc ren:
- B-íc ren ®-îc c¾t vµ b-íc vÝt me cã cïng hÖ thèng
®o l-êng (nh- cïng lµ ren Quèc tÕ hay ren Anh)  vÒ
nguyªn t¾c lµ kh«ng cã sai sè.
- Çc trÞ sè 25,4 vµ sè  ®-îc thay b»ng ç ph©n sè
t-¬ng ®-¬ng, ®¶m b¶o sai sè nhá nhÊt.
- Mçi mét lo¹i ren chØ cÇn kiÓm tra mét b-íc, nÕu tho¶
m·n th× çc b-íc cßn l¹i sÏ tho¶ m·n.
VÝ dô: C¾t ren Anh cã n = 4
 tp = 25,4/n = 25,4/4 = 6,350 mm
- Tõ b¶ng s¾p ren cña ren Anh,  Zn = 32, igb=1/2

84
 
60 42 42 28 36 1
1. . . . . . .12 6,3504 mm
60 42 50 25 32 2
 Ptx®:
 Sai sè b-íc ren: tp = 6,3504 – 6,350 = 0,004 (mm)
Sai sè b-íc ren ph¶i ®¶m b¶o: ‰, ‰0

Ch-¬ng 2
ThiÕt kÕ ®éng lùc häc m¸y c¾t kim lo¹i
1. X¸c ®Þnh chÕ ®é t¶i träng vµ c«ng
suÊt ®éng c¬ ®iÖn
2. TÝnh th©n m¸y
3. §-êng h-íng

86
1. X¸c ®Þnh chÕ ®é t¶I träng vµ c«ng suÊt
®éng c¬ ®iÖn
1.1 ChÕ ®é lµm viÖc giíi h¹n cña m¸y.
ChÕ ®é c¾t gät, chÕ ®é b«i tr¬n lµm l¹nh, an toµn,…
Ph¶i qui ®Þnh chÕ ®é lµm viÖc cña m¸y tr-íc khi
®-a vµo sö dông. X¸c ®Þnh chÕ ®é c¾t gät giíi h¹n
cña m¸y lµm c¬ së tÝnh to¸n ®éng lùc häc m¸y c¾t
kim lo¹i.
C¸c ph-¬ng ph¸p x¸c ®Þnh chÕ ®é c¾t gät giíi h¹n:

87
1.1.1 ChÕ ®é lµm viÖc cùc ®¹i (chÕ ®é c¾t gät)
- X¸c ®Þnh chiÒu s©u c¾t tmax
- X¸c ®Þnh l-îng ch¹y dao Smax
- Tõ ®ã x¸c ®Þnh giíi h¹n tèc ®é: vmin  vmax
- Theo kinh nghiÖm:  3
max maxt C d
- Toµn bé ct m¸y lµm viÖc ë chÕ ®é t¶i träng cùc ®¹i  kÝch
th-íc chi tiÕt lín  träng l-îng m¸y t¨ng lªn
 Hép m¸y to ra
KÕt cÊu m¸y
kh«ng nhá
gän
Lóc nµy:
- Trªn thùc tÕ, Ýt khi c«ng nh©n cho m¸y lµm viÖc ë chÕ ®é cùc
®¹i
- §é cøng v÷ng, ®é bãng, ®é chÝnh x¸c vµ tr×nh ®é tay nghÒ,
kh«ng cho phÐp m¸y lu«n lµm viÖc víi chÕ ®é t¶i träng cùc
®¹i. V× vËy sÏ hîp lý nÕu chän chÕ ®é t¶i träng kh¸c.

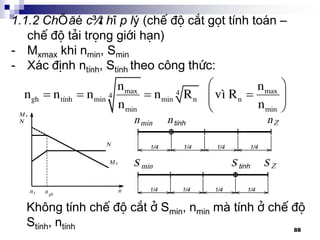
88
1.1.2 ChÕ ®é c¾t hîp lý (chÕ ®é c¾t gät tÝnh to¸n –
chÕ ®é t¶i träng giíi h¹n)
- Mxmax khi nmin, Smin
- X¸c ®Þnh ntÝnh, StÝnh theo c«ng thøc:
 
    
 
max max44
gh tÝnh min min n n
min min
n n
n n n n R v× R
n n
Kh«ng tÝnh chÕ ®é c¾t ë Smin, nmin mµ tÝnh ë chÕ ®é
StÝnh, ntÝnh

89
1.1.3 ChÕ ®é c¾t thö:
- ChÕ ®é c¾t thö do ng-êi thiÕt kÕ hay nhµ m¸y chÕ
t¹o m¸y quy ®Þnh
- Lµ c¬ së ®Ó ng-êi thiÕt kÕ tÝnh to¸n søc bÒn c¸c ctm
- Khi thiÕt kÕ m¸y míi ph¶i dùa theo 1 sè m¸y chuÈn
t-¬ng tù vµ chän chÕ ®é c¾t gät thö cña m¸y t-¬ng
tù ®Ó tÝnh ®éng lùc häc cho m¸y.
- ChÕ ®é c¾t thö m¸y v¹n n¨ng th«ng dông (xem phô
lôc).
- VÝ dô:
- M¸y tiÖn: ph«i thÐp C45, 70 x 350, chèng t©m
- Dao 450 – T15K6, n = 400 vg/ph, S = 0,39 mm/vg
t = 5 mm
- L¾p W ®Ó ®o c«ng suÊt. Kq: NC = 6,5 – 7 kW
(th-êng Nc¾t = (0,7 – 0,8)N®/c )

90
1.2 C«ng suÊt ®éng c¬ ®iÖn:
1.2.1 C«ng suÊt truyÒn dÉn chÝnh (xÝch Hép tèc ®é)
- C«ng suÊt ®éng c¬: N®/c = Nc + Nck + Nfô
Trong ®ã: - Nc - C«ng suÊt c¾t
- Nck- C«ng suÊt ch¹y kh«ng
- Nfô- C«ng suÊt phô
  Z
C
P .v
N kW
60.102.9,81
  C ®/cTh«ng thêng: N 0,7 0,8 N
  C
®/c
N
N
 hiÖu suÊt chung cña truyÒn dÉn
- C«ng suÊt ch¹y kh«ng: Nck = f(n).
   tb
ck m 1 tc6
d
N K . n K n
10
- C«ng suÊt c¾t:

91
- Km – hÖ sè phô thuéc chÊt l-îng chÕ t¹o çc chi
tiÕt, ®iÒu kiÖn b«I tr¬n, lÊy Km = 3  6.
- dtb - ®-êng kÝnh trung b×nh cña tÊt c¶ çc ngâng
trôc cña m¸y (mm) (khi thiÕt kÕ ®· tÝnh s¬ bé)
- n(vg/ph) – tæng sè vßng quay cña tÊt c¶ çc trôc,
trõ trôc chÝnh
- K1 – HÕ sè tæn thÊt c«ng suÊt riªng t¹i trôc chÝnh,
K1 = 1,5 nÕu æ trôc chÝnh lµ l¨n, = 2 nÕu lµ tr-ît
- ntc (vg/ph) – sè vßng quay trôc chÝnh
C«ng suÊt phô:   
k
fô ®/c k k
1
N N i 1
- k – hiÖu suÊt çc bé truyÒn cïng lo¹i (®ai, br,…)
- ik – sè l-îng çc bé truyÒn cïng lo¹i

92
VËy c«ng suÊt ®éng c¬:
 


 
C ck
®/c k
k k
1
N N
N
1 i 1
1.2.2 C«ng suÊt truyÒn dÉn ch¹y dao (2 ph-¬ng ph¸p)
a) TÝnh theo tû lÖ c«ng suÊt chÝnh (pp gÇn ®óng)
N®c
CD = K.N®c
chÝnh
§èi víi m¸y phay, c«ng suÊt ch¹y dao c«ng t¸c lµ 0,7
kW. Nh-ng do cã ch¹y dao nhanh nªn CS = 1,7 kW
b) TÝnh theo lùc chay dao cho phÐp (chÝnh x¸c h¬n)
M¸y tiÖn, khoan K = 0,04
M¸y phay K = 0,1  0,15
81,9..10.612
.
N 4
CD
SCD
dc
VQ


Q: lùc ch¹y dao cho phÐp (tra s¸ch)
CD = 0,15  0,2
VS - tèc ®é ch¹y dao

93
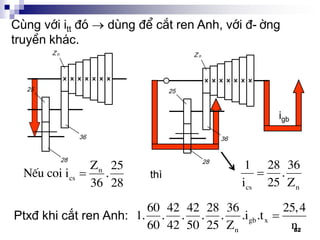
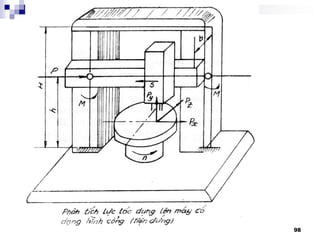
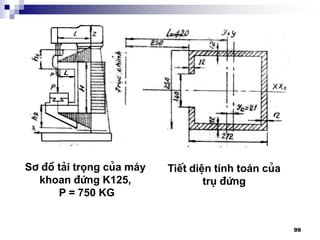
2. TÝnh th©n m¸y:
- Trô m¸y, sµ ngang, vá HT§, HCD,… Dïng ®Ó l¾p
c¸c bé phËn cña m¸y  m¸y
- Ph¶i ®¶m b¶o tÝnh æn ®Þnh khi lµm viÖc: biÕn d¹ng
Ýt, chèng rung ®éng,…
- Cøng v÷ng, ta quan t©m: - uèn f < [f]
- xo¾n  < []
- Th-êng chÕ t¹o b»ng gang x¸m: GX15 – 32, GX21 – 40
Cã thÓ b¨ng thÐp ®óc, thÐp hµn, m¸y h¹ng nÆng cã
thÓ lµ bª t«ng cèt thÐp
TiÕt diÖn ngang th©n m¸y

96
• §èi víi m¸y tiÖn, vÞ trÝ cña dao g©y xÊu nhÊt cho hÖ
thèng lµ:
• Pz, Px g©y uèn
• Py g©y xo¾n (thùc tÕ Pz còng g©y xo¾n, nh-ng nhá
nª ®-îc bá qua)
• TÝnh ®é vâng, gãc xoay.
/ 3a l

99
TiÕt diÖn tÝnh to¸n cña
trô ®øng
S¬ ®å t¶i träng cña m¸y
khoan ®øng K125,
P = 750 KG

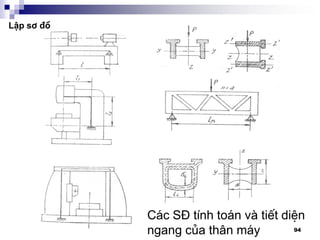
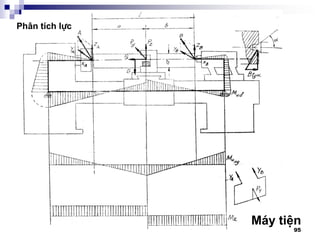
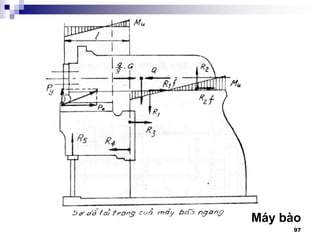
100
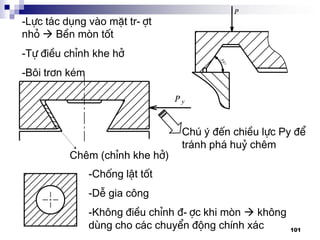
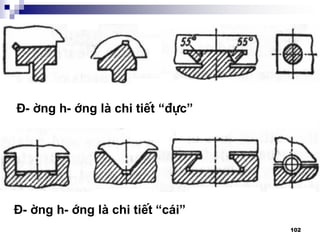
3. §-êng h-íng
3.1 §-êng h-íng tr-ît (sèng tr-ît):
Yªu cÇu:
- §¶m b¶o chÝnh x¸c
- §¶m b¶o ®é chÞu mµi mßn cao: tuæi thä.
®¶m b¶o ¸p suÊt p  [p]
Mßn Ýt nhÊt cña mét cÆp chuyÓn ®éng (c¬ khÝ) khi c¬
tÝnh cña chóng kh¸c nhau (vËt liÖu, ®é cøng, ph-¬ng
ph¸p gia c«ng,…)
VÝ dô: B¨ng m¸y ®-îc t«i, bµn m¸y kh«ng ®-îc t«i
C¸c d¹ng: -Kh¶ n¨ng t¶i tèt
-B«i tr¬n dÔ
-Mßn khã ®iÒu chØnh

101
-Lùc t¸c dông vµo mÆt tr-ît
nhá  BÒn mßn tèt
-Tù ®iÒu chØnh khe hë
-B«i tr¬n kÐm
Chªm (chØnh khe hë)
Chó ý ®Õn chiÒu lùc Py ®Ó
tr¸nh ph¸ huû chªm
-Chèng lËt tèt
-DÔ gia c«ng
-Kh«ng ®iÒu chØnh ®-îc khi mßn  kh«ng
dïng cho c¸c chuyÓn ®éng chÝnh x¸c

102
§-êng h-íng lµ chi tiÕt “®ùc”
§-êng h-íng lµ chi tiÕt “c¸i”

103
- VÝ dô:
§èi víi m¸y tiÖn:
DÉn h-íng cho
bµn dao
DÉn h-íng ô ®éng
Chèng lËt
ChuÈn ®Ó söa ch÷a

104
3.2 §-êng h-íng l¨n:
§Æc ®iÓm:
- Ma s¸t nhá
- T¶i träng nhá
Mét sè lo¹i:
a) Lo¹i më b) Lo¹i ®ãng kÝn

Ch-¬ng 3
®iÒu khiÓn b»ng c¬ khÝ – b«I tr¬n vµ lµm nguéi
1. §iÒu khiÓn b»ng c¬ khÝ
2. B«i tr¬n vµ lµm nguéi

106
1. ®iÒu khiÓn b»ng c¬ khÝ:
1.1 Yªu cÇu vµ chøc n¨ng
1.1.1 Chøc n¨ng:
§ãng më ®éng c¬ ®iÖn
§ãng më truyÒn ®éng chÝnh
§ãng më truyÒn ®éng ch¹y dao
Thay ®æi sè vßng quay vµ l-îng ch¹y dao,
®¶o chiÒu c¸ chuyÓn ®éng
§Þnh vÞ, kÑp chÆt, b«i tr¬n,…

107
1.1.2 Yªu cÇu:
An toµn
- Kho¸ liªn ®éng c¸c c¬ cÊu ®iÒu khiÓn (kh«ng ®ång
thêi ®ãng 2 chuyÓn ®éng)
- §Þnh vÞ c¬ cÊu ®iÒu khiÓn ë mçi vÞ trÝ cña nã.
H¹n chÕ hµnh tr×nh
§iÒu khiÓn ph¶i nhanh
1.1.3 Ph©n lo¹i:
G¹t ph©n t¸n  nhiÒu tay g¹t (g¹t tõng khèi b¸nh
r¨ng
G¹t tËp trung: Dïng mét tay g¹t ®Ó g¹t tÊt c¶ c¸c BR
(P82). Mét tay g¹t g¹t mét vµi khèi BR (T620)

108
1.2 HÖ thèng ®iÒu khiÓn c¬ khÝ cña m¸y:
Bao gåm 3 côm chñ yÕu sau:
- C¬ cÊu ®iÒu khiÓn: ®Ó ng-êi sd m¸y ®iÒu khiÓn
- C¬ cÊu trung gian
- C¬ cÊu chÊp hµnh: liªn hÖ trùc tiÕp víi c¸c khèi
BR di tr-ît.
G¹t riªng rÏ:

109
G¹t tËp trung: (chó ý ®Õn hµnh trÝnh g¹t)
 C¸c tÝnh to¸n cô thÓ khi thÓ khi thiÕt
kÕ:
- X¸c ®Þnh hµnh tr×nh g¹t
- C¸c tÝnh to¸n cô thÓ cho 1 sè
cµng g¹t, cam g¹t ®iÓn h×nh
- LËp b¶ng chu kú g¹t, vÏ ®-êng
khai triÓn cña cam
Ltr = B + f
Lph = B1 + f

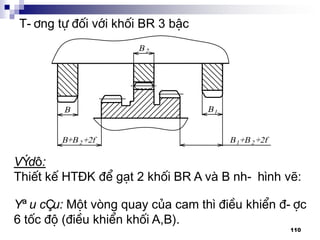
110
VÝ dô:
ThiÕt kÕ HT§K ®Ó g¹t 2 khèi BR A vµ B nh- h×nh vÏ:
T-¬ng tù ®èi víi khèi BR 3 bËc
Yªu cÇu: Mét vßng quay cña cam th× ®iÒu khiÓn ®-îc
6 tèc ®é (®iÒu khiÓn khèi A,B).

111
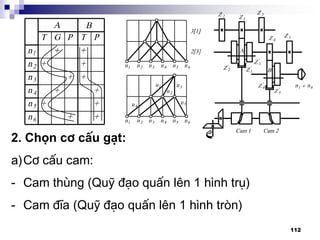
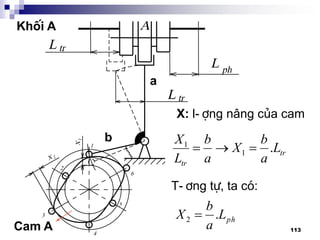
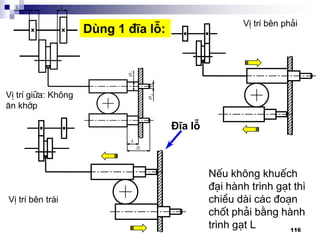
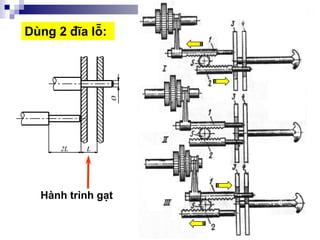
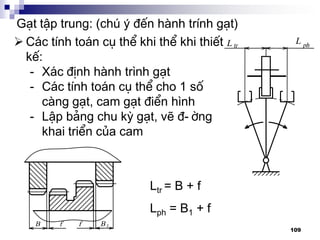
1. Thµnh lËp chu kú g¹t:
C¬ së: dùa vµo l-íi kÕt cÊu,
®å thÞ vßng quay vµ kÕt cÊu
cô thÓ:
PAKG: Z = 3 x 2
I II
[1] [3]

2. Chän c¬ cÊu g¹t:
a)C¬ cÊu cam:
- Cam thïng (Quü ®¹o quÊn lªn 1 h×nh trô)
- Cam ®Üa (Quü ®¹o quÊn lªn 1 h×nh trßn)
112

114
Cam B
Cam B ®-îc thiÕt kÕ t-¬ng tù
Sau khi thiÕt kÕ ®-îc 2 cam, 2
cam sÏ ®-îc l¾p trªn cïng
mét trôc. b
a
Acsimet
L-îng n©ng cña cam:
L
a
b
X .
§èi víi cam thïng?

115
b)§Üa lç:
- Dïng 1 ®Üa lç (chèt ph¶i cã bËc).
- Dïng 2 ®Üa lç
C¬ cÊu ®iÒu khiÓn dïng ®Üa lç M¸y 6M82
VÝ dô:

116
Dïng 1 ®Üa lç:
NÕu kh«ng khuÕch
®¹i hµnh tr×nh g¹t th×
chiÒu dµi c¸c ®o¹n
chèt ph¶i b»ng hµnh
tr×nh g¹t L
VÞ trÝ gi÷a: Kh«ng
¨n khíp
VÞ trÝ bªn ph¶i
VÞ trÝ bªn tr¸i
§Üa lç

117
Dïng 2 ®Üa lç:
Hµnh tr×nh g¹t

118
Hµnh tr×nh g¹t ®-îc khuÕch ®¹i
Z0
Z
0
11
0
.Z
L
L
Z
L
L
Z
Z

L – Hµnh tr×nh c¬ së
L1 – Hµnh tr×nh g¹t

119
Phô lôc1:
T×m sè r¨ng c¸c Br nhãm c¬ së HCD dïng Br di tr-ît:
i
cs '
i
Z a.A
i
Z a.B
  Trong
®ã:  x x
Z
a ¯ mét sè nguyªn
f g



l
VÝ dô: Z = 78, (fx + gx) = 19  a = 78/19  4
cs
9 4.9 36
i
10 4.10 40
   
Nếu ô nào không tìm được số a thì ta bỏ trống. Mỗi a
tìm được như vậy, ta tính số răng và điền vào Bảng
Chọn các cặp ô cùng hàng ngang liền nhau có cùng
tử (hoặc mẫu) ghép thành một đôi (có 3 Br) tạo ra
3 TST

120
Phô lôc 2: Tû sè thay cho: 25,4 vµ sè 
Tû sè Sai sè
Thùc tÕ = 0
-0,013
+0,046
-0,061
127
25,4
5

1600 40.40
25,4
63 7.9
 
432 18.24
25,4
17 17
 
330 11.30
25,4
13 13
 

121
TT TrÞ sè b»ng c¸c ph©n
sè
Sai sè Chó ý
1 -0,0005 CÇn Br Z = 47 hay Z = 97.
Dïng ®Ó c¾t ren M«®un
khi vÝt me theo hÖ Anh
2 +0,021
3 +0,004 CÇn Br Z = 127, th-êng
dïng ®Ó c¾t ren M«®un
khi vitme lµ Quèc tÕ, hoÆc
c¾t ren Pit khi vitme lµ ren
Quèc tÕ hoÆc ren Anh
4 +0,04 Kh«ng cÇn Br ®Æc biÖt
nµo
5 -0,05 CÇn Br thay thÕ Z = 157
47 127 47.127
.
380 5 4.5.95
  
12.127
97.5
 
19.21
127
 
22
7
 
157
50
 

122
Phô lôc 3: ChÕ ®é c¾t gät cùc ®¹i:
Trong ®ã C = 0,7 ®èi víi thÐp.
dmax - ®-êng kÝnh cùc ®¹i cña chi tiÕt gia c«ng
(kh«ng sö dông cho m¸y mµi vµ c¸c m¸y cã c®
chÝnh lµ th¼ng)
 3
max maxt C d
 
  
 
min max
1 1
t t
2 4
 
  
 
min max
1 1
S t
5 10
 
  
 
max max
1 1
S t
3 7
 v v
vmin
min X y
max max
C
V
t .S
 v v
vmax
max X y
min min
C
V
t .S

123
 = a.
§èi víi cam thïng: L = X
C¸ch vÏ ®-êng Acsimet

Thiết kế máy công cụ

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Viewers also liked

Viewers also liked (18)

Similar to Thiết kế máy công cụ

Similar to Thiết kế máy công cụ (20)

More from Trung Thanh Nguyen

More from Trung Thanh Nguyen (19)

Recently uploaded

Recently uploaded (20)

Thiết kế máy công cụ