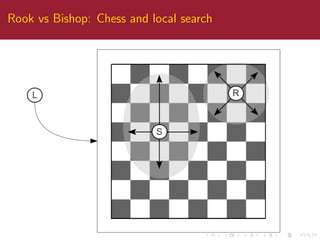
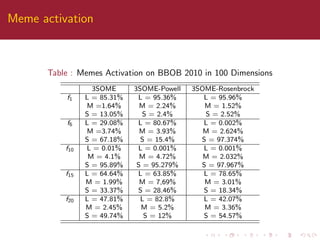
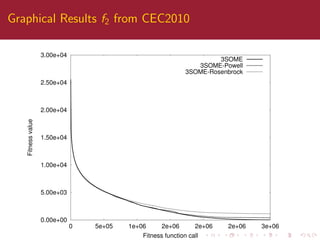
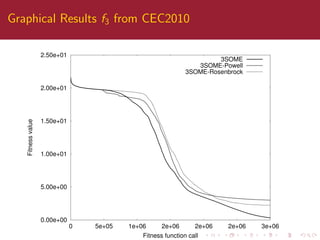
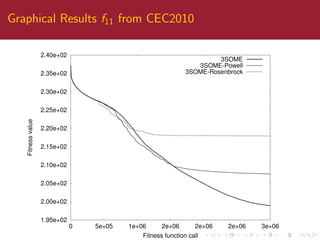
This paper compares different local search algorithms within the three stage optimal memetic exploration (3SOME) sequential structure. 3SOME normally uses steepest descent local search (S) as the third stage, but this is replaced with Rosenbrock and Powell algorithms to test the importance of the structure. Results show the meme activation rates vary slightly but performance is generally similar, indicating the sequential structure is important alongside the specific local search methods. The paper concludes algorithm structure is as important as the individual components and future automatic design should consider both.

1. The Importance of Being Structured
a Comparative Study on Multi Stage Memetic Approaches
Fabio Caraffini, Giovanni Iacca, Ferrante Neri, and Ernesto Mininno
CCI, De Montfort University, United Kingdom
INCAS3 The Netherlands
University of Jyv¨askyl¨a, Finland
05.09.2012 (UKCI2012, Edinburgh)

2. Outline
Background
Ockham’s Razor and Multiple Stage Optimal Memetic
Exploration
Sequential Structure
Local search logics within sequential structure
The importance of the structure
Numerical Results
Conclusion

3. Background
Memetic Algorithm (MA): evolutionary framework + one or
more local search components
Memetic Computing (MC): structured set of heterogeneous
components for solving problems
Ockham’s Razor in MC: simple algorithms can display a
performance which is as good as that of complex algorithms 1
Three Stage Optimal Memetic Exploration (3SOME):
Sequential structure composed of three components that
progressively perturb a single solution
1
G. Iacca, F. Neri, E. Mininno, Y.S. Ong, M.H. Lim, Ockham’s Razor in
Memetic Computing: Three Stage Optimal Memetic Exploration, Informa-
tion Sciences, Elsevier, Volume 188, pages 17-43, April 2012

4. The 3SOME algorithm: algorithmic components
The current best solution is named elite xe while a trial
solution is named xt
Long distance exploration (L): at first a solution xt is
randomly generated and then the exponential crossover
(Differential Evolution) with xe is applied
Middle distance exploration (M): a hypercube of side δ,
centred around the solution xe, is constructed and the trial
point xt is generated within the hypercube
Short distance exploration (S): a steepest descent local
search attempts to improve upon xe by separately perturbing
each variable

5. The 3SOME algorithm: algorithmic structure
L is continued until a new promising solution found
M is continued while successful
S is performed and, if successful, activates M, if fails,
activates L
Note: S stands for Success and F for Failure

6. Sequential structures
Composed of a set of algorithmic components (memes)
A solution (or a population) is progressively perturbed by each
component
A set of condition determines which component is activated
for the subsequent perturbation

7. What is this paper about?
We attempted to study the sequential structure by removing
S and replacing it with other local search algorithms
Research Question: What happens to the performance If we
remove S and replace it with another local search logic?
(Implicit) Research Question: How much is the structure
important with respect to the memes composing it?

8. Short distance exploration (S)
The variables are perturbed one-by-one
For each coordinate i, xs[i] = xe[i] − ρ (ρ exploratory radius)
If xs outperforms xe, the trial solution xt is updated
Otherwise a half step in the opposite direction
xs[i] = xe[i] + ρ
2 is performed
xs replaces xt if it outperforms xe

9. Rosenbrock Algorithm 2
For each coordinate i, with an initial step size h, the variables
are perturbed
In case of success, the step size is increased of a factor α,
otherwise decreased of β and the opposite direction is tried
The coordinate system is rotated towards the
approximated gradient, the step size is reinitialized and the
procedure is repeated
2
H. H. Rosenbrock, An automatic method for finding the greatest or least
value of a function, The Computer Journal, vol. 3, no. 3, pp. 175-184,1960

10. Powell Algorithm3
n separate minimisations are performed along n different
directions
Along each direction (in this study) the Golden Section Search
is performed
The directions are taken linearly independent
3
M. J. D. Powell, An efficient method for finding the minimum of a function
of several variables without calculating derivatives, The Computer Journal,
vol. 7, no. 2, pp. 155-162, Jan. 1964.

11. Rook vs Bishop: Chess and local search

12. Experimental Setup
BBOB20104 at 10,20, and 40 dimensions
CEC20105 at 1000 dimensions
100 runs, each of them has been performed for 5000 × n
fitness evaluations
The original 3SOME algorithm has been compared with their
versions where S is replaced by Rosenbrock and Powell
methods, respectively
4
N. Hansen, A. Auger, S. Finck, R. Ros et al., Real-parameter black- box
optimization benchmarking 2010: Noiseless functions definitions, INRIA,
Tech. Rep. RR-6829, 2010
5
K. Tang, X. Li, P. N. Suganthan, Z. Yang, and T. Weise, Benchmark func-
tions for the cec2010 special session and competition on large-scale global
optimization, University of Science and Technology of China (USTC), Tech.
Rep., 2010

13. Meme activation
Table : Memes Activation on BBOB 2010 in 100 Dimensions
3SOME 3SOME-Powell 3SOME-Rosenbrock
f1 L = 85.31% L = 95.36% L = 95.96%
M =1.64% M = 2.24% M = 1.52%
S = 13.05% S = 2.4% S = 2.52%
f6 L = 29.08% L = 80.67% L = 0.002%
M =3.74% M = 3.93% M = 2.624%
S = 67.18% S = 15.4% S = 97.374%
f10 L = 0.01% L = 0.001% L = 0.001%
M = 4.1% M = 4.72% M = 2.032%
S = 95.89% S = 95.279% S = 97.967%
f15 L = 64.64% L = 63.85% L = 78.65%
M = 1.99% M = 7,69% M = 3.01%
S = 33.37% S = 28.46% S = 18.34%
f20 L = 47.81% L = 82.8% L = 42.07%
M = 2.45% M = 5.2% M = 3.36%
S = 49.74% S = 12% S = 54.57%

14. Graphical Results f2 from CEC2010
0.00e+00
5.00e+03
1.00e+04
1.50e+04
2.00e+04
2.50e+04
3.00e+04
0 5e+05 1e+06 2e+06 2e+06 2e+06 3e+06
Fitnessvalue
Fitness function call
3SOME
3SOME-Powell
3SOME-Rosenbrock

15. Graphical Results f3 from CEC2010
0.00e+00
5.00e+00
1.00e+01
1.50e+01
2.00e+01
2.50e+01
0 5e+05 1e+06 2e+06 2e+06 2e+06 3e+06
Fitnessvalue
Fitness function call
3SOME
3SOME-Powell
3SOME-Rosenbrock

16. Graphical Results f11 from CEC2010
1.95e+02
2.00e+02
2.05e+02
2.10e+02
2.15e+02
2.20e+02
2.25e+02
2.30e+02
2.35e+02
2.40e+02
0 5e+05 1e+06 2e+06 2e+06 2e+06 3e+06
Fitnessvalue
Fitness function call
3SOME
3SOME-Powell
3SOME-Rosenbrock

17. Summary of the Results
The meme activation scales up with the dimensionality
(percentages are nearly constant for various dimensionality
values)
The meme activation slightly changes with the short distance
meme (e.g. a separable function makes use of S)
The performance of the 3SOME variants is very similar
for low dimensions (up to 100D)
For large scale problems, the performance is diverse in
some cases and similar in others

18. Remarks and Future Works
3SOME sequential structure displays a high performance even
when a meme is replaced
Algorithms composed of different memes but sharing the same
structure may have a similar behaviour
The structure of an algorithm is as important as the
memes/operators that compose it
Future automatic design of algorithms should properly select
the memes and ALSO combine them according to a proper
structure/logic

19. Thanks for your attention!