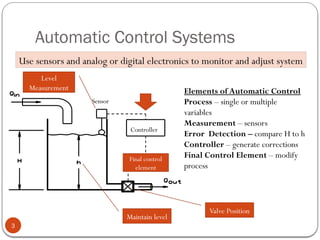
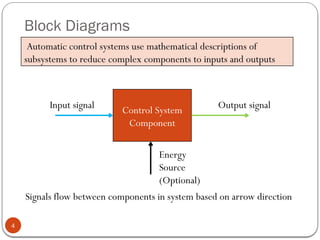
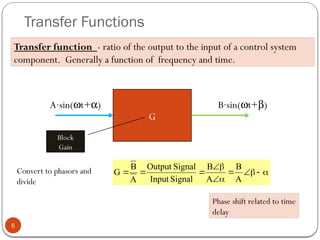
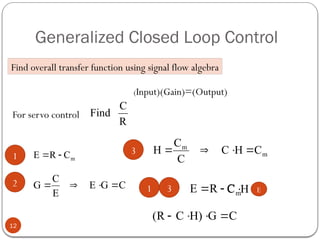
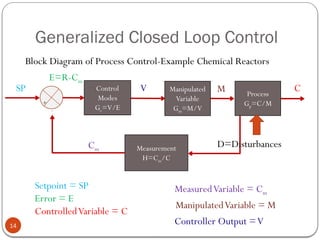
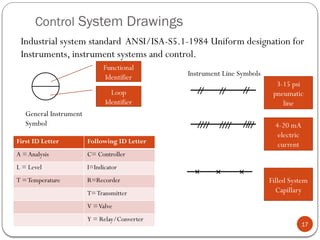
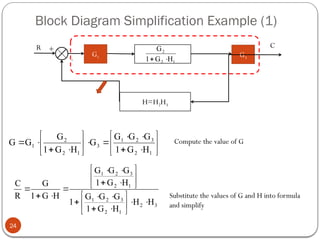
The document discusses fundamental control concepts, focusing on maintaining process variables at desired values while counteracting external disturbances. It distinguishes between open-loop and closed-loop control systems and emphasizes the importance of feedback mechanisms in automatic control systems. Additionally, it covers transfer functions, block diagrams, and the simplification of control system components for effective process control.