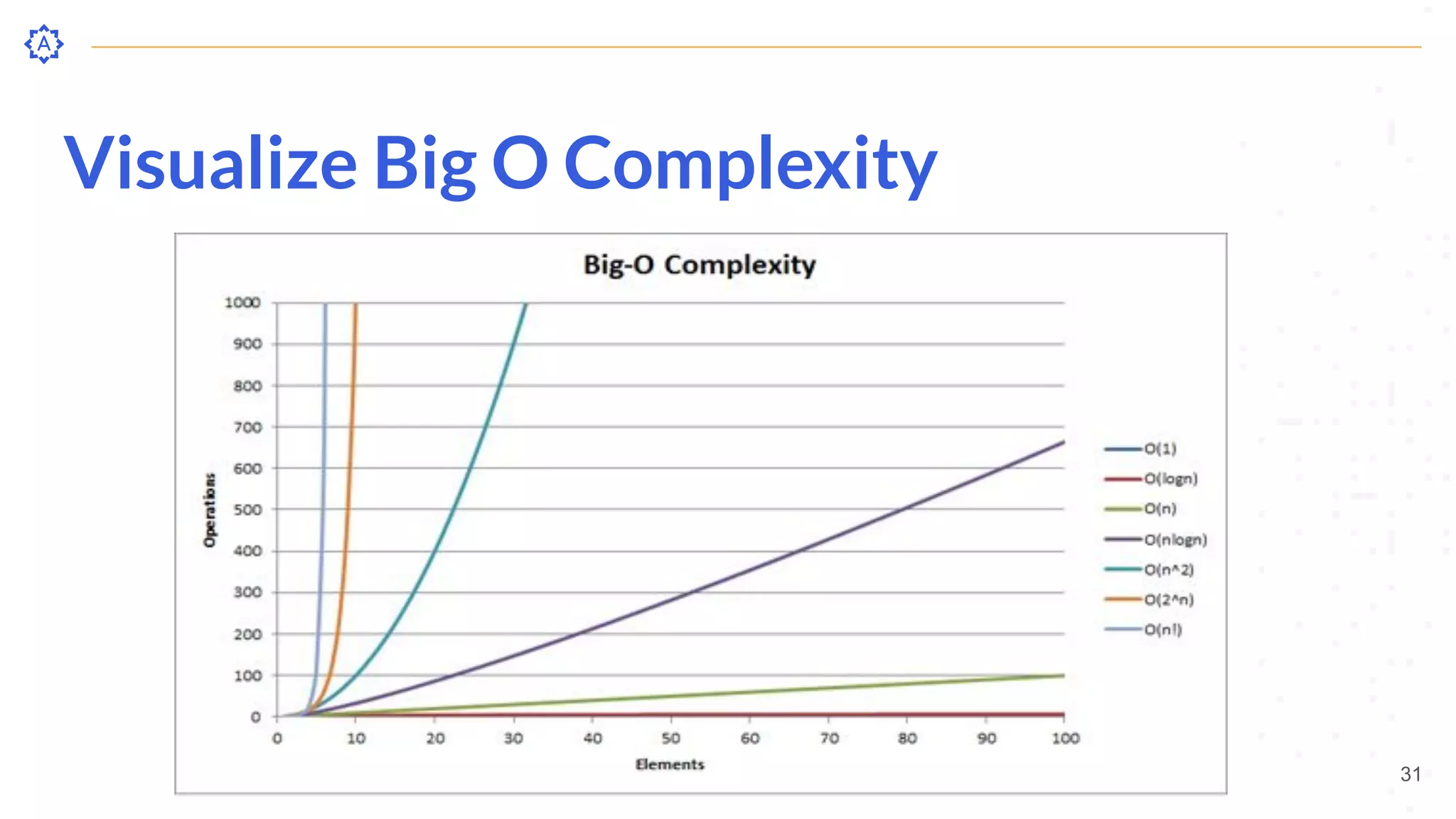
The document presents an overview of Big O notation, which is a method for analyzing the efficiency of algorithms as data size increases. It explains the importance of understanding code performance, efficiency trade-offs, and includes examples of different algorithms along with their corresponding Big O complexities. Additionally, it covers common Python operations and their complexities.

1. The Big O with Python
Learn how to analyze code for efficiency
1
Presented by: Dennis Wainaina
Position: Senior Software Engineer

2. What’s Big O?
2

3. What’s Big O?
- How your code performs as you process more data
3

4. What’s Big O?
- How your code performs as you process more data
- It’s NOT running time
4

5. What’s Big O?
- How your code performs as you process more data
- It’s NOT running time
- General trend of performance over time
5

6. What’s Big O?
- How your code performs as you process more data
- It’s NOT running time
- General trend of performance over time
- A way of ranking the efficiency of an algorithm
6

7. Why Care?
7

8. Why Care?
- Provides a formal way to talk about how your code
performs in comparison to your data
8

9. Why Care?
- Provides a formal way to talk about how your code
performs in comparison to your data
- Discussing trade-offs between different approaches
9

10. Why Care?
- Provides a formal way to talk about how your code
performs in comparison to your data
- Discussing trade-offs between different approaches
- When you notice your code is slowing down and want
to find the bottlenecks
10

11. Why Care?
- Provides a formal way to talk about how your code
performs in comparison to your data
- Discussing trade-offs between different approaches
- When you notice your code is slowing down and want
to find the bottlenecks
- INTERVIEWS 😂
11

12. Terminology
- O stands for “Order of”
12

13. Terminology
- O stands for “Order of”
- N represents how much data you got
13

14. Some Examples
14

15. Some Examples
Write a function that calculates the sum of integers from 1
to n
15

16. Some Examples
def add_one_to_n(n):
total = 0
i = 1
while i <= n:
total += i
i += 1
return total
16

17. Some Examples
def add_one_to_n_mathematical(n):
return n * (n + 1) / 2
17

18. So, which one is better?
18
Instead of timing, we can count the number of operations
performed by each piece of code

19. Let’s count the steps
def add_one_to_n_mathematical(n):
return n * (n + 1) / 2
19
1 multiplication
1 addition
1 division

20. Let’s count the steps
def add_one_to_n_mathematical(n):
return n * (n + 1) / 2
20
1 multiplication
1 addition
1 division
3 steps regardless of the
size of n

21. Let’s count the steps
def add_one_to_n(n):
total = 0
i = 1
while i <= n:
total += i
i += 1
return total
21
n additions
1 assignment
1 assignment
n comparisons

22. Let’s count the steps
- 2n ?
- 3n + 2 ?
- 5n + 2 ?
😩 22

23. Big O!
- 2n -> O(n)
- 3n + 2 -> O(n)
- 5n + 2 -> O(n)
- O(3) -> O(1)
- O(n + n2
) -> O(n2
)
- O(7n4
+ 2n2
+ 5) -> ???
23

24. Big O!
So, add_one_to_n_mathematical is O(1) and
add_one_to_n is O(n)
24

25. A O(n2
) Example
def pairs(n):
for i in range(n):
for j in range(n):
print(i, j)
25

26. A O(n2
) Example
26
def pairs(n):
for i in range(n): O(n)
for j in range(n):
O(n)
print(i, j)

27. A O(n2
) Example
def pairs(n):
for i in range(n): O(n)
for j in range(n):
O(n)
print(i, j)
27
Nested O(n)
operations!!!
O(n * n) = O(n2
)

28. A O(log n) Example
def binary_search(arr, elem):
start = 0
end = len(arr) - 1
middle = math.floor((start + end) / 2)
while arr[middle] != elem:
if elem < arr[middle]:
end = middle - 1
else:
start = middle + 1
if start >= end:
return -1
middle = math.floor((start + end) / 2)
return middle
28

29. Common Python Operations
29
Lists
my_list.appen
d(a)
O(1)
my_list[i] O(1)
val in my_list O(1)
for val in
my_list
O(n)
my_list.sort() O(nlogn)
Sets
my_set.add(va
l)
O(1)
For val in
my_set
O(n)
val in my_set O(1)

30. Common Python Operations
30
Dicts
my_dict[key] = val O(1)
my_dict[key] O(1)
key in my_dict O(1)
for key in my_dict O(n)

31. Visualize Big O Complexity
31

32. <Thanks>
32