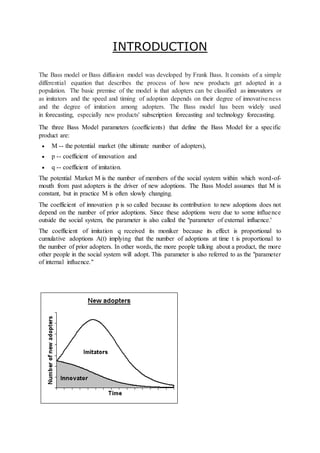
The document discusses using the Bass diffusion model to analyze subscription data from Aakash Institute. The model was used to determine the coefficients of innovation, imitation, and market potential. The results found that word of mouth increased subscriptions over time as P < Q, and that the later subscription decline appeared steady. This led Byju's to decide acquiring Aakash could provide a competitive advantage by leveraging existing educational ties.

1. INTRODUCTION
The Bass model or Bass diffusion model was developed by Frank Bass. It consists of a simple
differential equation that describes the process of how new products get adopted in a
population. The basic premise of the model is that adopters can be classified as innovators or
as imitators and the speed and timing of adoption depends on their degree of innovativeness
and the degree of imitation among adopters. The Bass model has been widely used
in forecasting, especially new products' subscription forecasting and technology forecasting.
The three Bass Model parameters (coefficients) that define the Bass Model for a specific
product are:
 M -- the potential market (the ultimate number of adopters),
 p -- coefficient of innovation and
 q -- coefficient of imitation.
The potential Market M is the number of members of the social system within which word-of-
mouth from past adopters is the driver of new adoptions. The Bass Model assumes that M is
constant, but in practice M is often slowly changing.
The coefficient of innovation p is so called because its contribution to new adoptions does not
depend on the number of prior adoptions. Since these adoptions were due to some influence
outside the social system, the parameter is also called the "parameter of external influence.'
The coefficient of imitation q received its moniker because its effect is proportional to
cumulative adoptions A(t) implying that the number of adoptions at time t is proportional to
the number of prior adopters. In other words, the more people talking about a product, the more
other people in the social system will adopt. This parameter is also referred to as the "parameter
of internal influence."

2. PROBLEM STATEMENT
During 2021, Byju’s, the Learning App, thought of acquiring an educational/coaching institute
namely the Aakash Institute, after they had successfully acquired another online Learning App
namely, White Hat Junior.
Byju’s, the Learning App, wanted to carry out more analysis of what is the present market
demand, before progressing with this plan of acquiring Aakash Institute. Therefore, the Aakash
Institute, was asked to provide their monthly subscription data. The below data was provided
to Byju’s, the Learning App, by Aakash Institute:
Months Students
Subscription
1 0.593
2 0.976
3 1.207
4 1.221
5 1.457
6 1.952
7 2.307
8 2.542
9 3.131
10 3.167
11 3.397
12 3.743
13 3.936
14 4.125
15 4.268
16 4.651
17 4.665
18 4.817
19 4.870
20 4.889
21 4.898
22 5.205
23 5.280
24 5.621
25 6.100
Months Students
Subscription
26 6.172
27 5.422
28 5.350
29 4.871
30 4.530
31 4.455
32 4.148
33 4.139
34 4.120
35 4.067
36 3.915
37 3.901
38 3.518
39 3.375
40 3.186
41 2.993
42 2.647
43 2.417
44 2.381
45 1.792
46 1.557
47 1.202
48 0.707
49 0.471
50 0.157

3. METHODOLOGY
The Bass diffusion model has been utilized, in Excel, in order to address this problem.
The are 3 parameters that we need to find out from this problem, are as below:
1. Coefficient of innovation(p)
2. Coefficient of imitation(q)
3. Coefficient of market potential(m)
While trying to find the above-mentioned values, we also need to keep in mind and make
sure that the Error squared value (E2) has to be minimum. In order to do so, we have taken
the help of Solver in Excel, choosing the solving method as evolutionary.
We already have the Actual Subscription data available with us. Next, we have calculated the
cumulative subscription in column N in the attached excel sheet. Now we have used the Bass
Diffusion Model, we have calculated the predicted subscription data with the below
mentioned formula:
D =(P+Q*(N/M))*(M-N)
where,
P- Coefficient of innovation
Q- Coefficient of imitation
M- Coefficient of market potential
N- Cumulative Subscription
Now, we have the predicted subscription of every month available with us.
We did this to find the predicted subscription data for all the quarters. Following that, we
determined the error as well as the Error square value (E2).
Error(E)= C-D
Error Square(F)= E^2
where,
C- Actual Subscription
D- Predicted Subscription
E- Error
The total of all the error square values has been calculated in the F57 cell using the formula
below.

4. =SUM(F7:F56)
Our primary goal is to minimize the sum of error square value by changing the three
coefficients p, q and m.
The following constraints in Solver, to resolve this problem:
 M <= 500
 M >= 0
 P <= 1
 P >= -1
 Q <= 1
 Q >= -1

5. RESULTS AND FINDINGS
We have obtained the following result after solving with the above-mentioned constraints:
Co-efficient of innovation p 0.00766285
Co-efficient of imitation q 0.10885027
Co-efficient of market
potential
m 179.042271
Sum of error squared 7.351
Bass Diffusion Model
0.000
1.000
2.000
3.000
4.000
5.000
6.000
7.000
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49
SUBSCRIPTION
MONTHS
Chart Title
Actual Sales Predicted Sales

6. CONCLUSION
Usingthe Bass Model,we discoveredthe below points:
1. The decline in subscription rangingfromthe 27th to the 50th monthappearedtobe steady
rather thansudden.Asa result,we mayconclude that initially the subscriptionwaswell
receivedbystudents.
2. In the situationwhenP < Q, itimpliesthatwordof mouth has increasedthe subscriptionof
the AakashInstitute.Atfirst,justafew people appliedforsubscription,butlateronthe
subscriptionwasoptedbymore numberof people.
Byjus,the LearningApp decided toacquire Aakash, basedonthe aforementionedfindings. The Byjus
Managementbelievedthatbyleveragingitstieswith othereducationalinstitutions,they wouldbe
able to gaina competitive advantageinthe market.