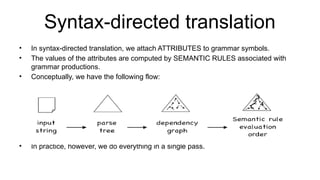
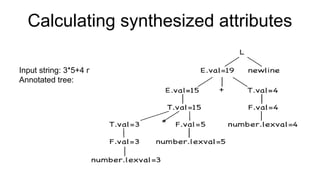
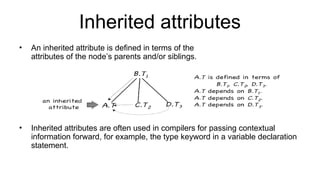
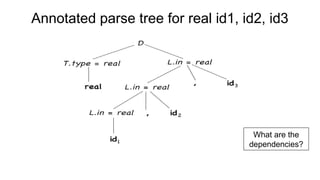
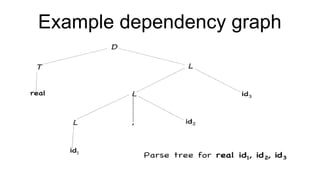
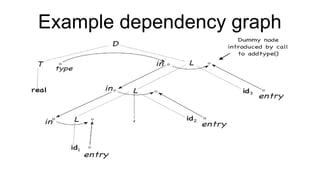
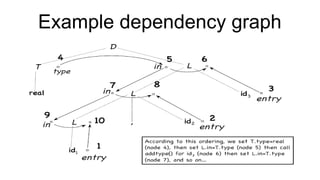
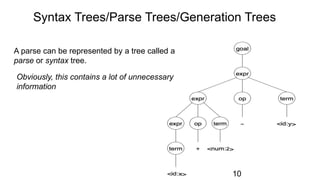
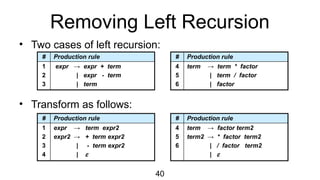
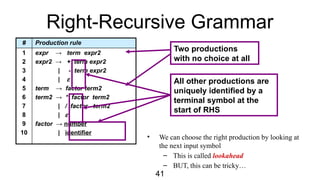
The document discusses syntactic analysis, focusing on context-free grammars (CFG) and parsing techniques. It covers various parsing methods, including top-down and bottom-up parsing, and examines the importance of grammar forms like LL(1) and LR(1). Additionally, it highlights concepts like ambiguity in grammar, syntax-directed translation, and syntactic translation using attributes.

1. Syntactic Analysis
int* foo(int i, int j))
{
for(k=0; i j; )
fi( i > j )
return j;
}
extra parenthesis
Missing
expression
not a keyword

2. Syntactic Analysis
int* foo(int i, int j)
{
for(k=0; i < j; j++ )
if( i < j-2 )
sum = sum+i
return sum;
}
undeclared var
return type
mismatch
undeclared var
return type
mismatch

3. Syntax Analysis
Every PL has rules for syntactic structure.
The rules are normally specified by a CFG (Context-Free Grammar) or BNF
(Backus-Naur Form)
Usually, we can automatically construct an efficient parser from a CFG or BNF.
Grammars also allow SYNTAX-DIRECTED TRANSLATION.

4. - Natural language analogy: consider the sentence
He Wrote The Program
Syntactic Analysis
noun verb article noun

5. Programming language
Syntactic Analysis
if ( b <= 0 ) a = b
Boolean exp assignment
If-statement

6. Context-Free Grammars
The mathematical model of a grammar is:
G = (S,N,T,P)
• S is the start-symbol
• N is a set of non-terminal symbols
• T is a set of terminal symbols
• P is a set of productions — P: N  (N T)*
A grammar is called RECURSIVE if it permits derivations of the form
Aw1Aw2
More specifically, it is called LEFT RECURSIVE if
AAw2
And RIGHT RECURSIVE
Aw1A
6

7. Context-Free Grammars
Context-free syntax is specified with a grammar, usually in Backus-Naur form
(BNF).
In BNF production have the form
Left side  definition
Where left-side contain one non-terminal
Left side ^ N = null
Let production for any grammar are:
SaSa
SbSb
Sc
7

8. Context-Free Grammars
1. <goal> := <expr>
2. <expr> := <expr> <op> <term>
3. |
<term>
4. <term> := number
5. | id
6. <op> := +
7. | -
8

9. Deriving Valid Sentences
Production Result
<goal>
1 <expr>
2 <expr> <op> <term>
5 <expr> <op> y
7 <expr> - y
2 <expr> <op> <term> - y
4 <expr> <op> 2 - y
6 <expr> + 2 - y
3 <term> + 2 - y
5 x + 2 - y
Given a grammar, valid
sentences can be derived by
repeated substitution.
To recognize a valid sentence in
some CFG, we reverse this
process and build up a parse.
9

10. Syntax Trees/Parse Trees/Generation Trees
A parse can be represented by a tree called a
parse or syntax tree.
Obviously, this contains a lot of unnecessary
information
10

11. Abstract Syntax Trees
So, compilers often use an abstract syntax tree (AST).
ASTs are often used as an IR.
11

12. The Frontend
Parser Checks the stream of words and
their parts of speech (produced by the
scanner (LA)) for grammatical correctness
Determines if the input is syntactically well
formed
Guides checking at deeper levels than
syntax
Builds an IR representation of the code
Think of this as the mathematics of
diagramming sentences

13. Parsing
13
- Checks the stream of words and their parts of speech for
grammatical correctness
- Determines if the input is syntactically well formed
- Guides context-sensitive (“semantic”) analysis (type
checking)
- Builds IR for source program

14. Parsing- The big picture
14
Goal is a flexible parser generator system

15. Parsing Techniques
15
Top-down parser:
- starts at the root of derivation tree and fills in
- picks a production and tries to match the input
- may require backtracking
- some grammars are backtrack-free (predictive)
Bottom-up parser:
- starts at the leaves and fills in
- starts in a state valid for legal first tokens
- as input is consumed, changes state to encode possibilities (recognize valid
prefixes)
- uses a stack to store both state and sentential forms

16. Derivations

17. The Two Derivations for x – 2 * y
In both cases, Expr *
⇒ id – num * id
• The two derivations produce different parse trees
– Actually, each of two different derivations produces both parse trees as the grammar itself is
ambiguous
• The parse trees imply different evaluation orders!
Leftmost derivation Rightmost derivation

18. Derivations and Parse Trees
Leftmost derivation
This evaluates as x – ( 2 * y )

19. Derivations and Parse Trees
Rightmost derivation
This evaluates as ( x – 2 ) * y

20. Ambiguity
This sentential form has two derivations
if Expr1 then if Expr2 then Stmt1 else Stmt2
production 2, then
production 1
production 1, then
production 2

21. Ambiguity
Removing the ambiguity
• Must rewrite the grammar to avoid generating the problem
• Match each else to innermost unmatched if (common sense rule)
Intuition: a NoElse always has no else on its last
cascaded else if statement
With this grammar, the example has only one derivation

22. Ambiguity
if Expr1 then if Expr2 then Stmt1 else Stmt2
This binds the else controlling S2 to the inner if

23. 23
Exercises
What is Panic Mode?

24. Role of a Parser
24
•- Not all sequences of tokens are program.
-Parser must distinguish between valid and invalid
sequences of tokens.
- An expressive way to describe the syntax.
• - An acceptor mechanism that determines if input
token stream satisfies the syntax.

25. -Parsing is the process of discovering a derivation
for some sentence
-Mathematical model of syntax – a grammar G.
-Algortihm for testing membership in L(G).
Study of Parsing

26. 26
Two Approaches

27. 27
Grammars and Parsers
• LL(1) parsers
– Left-to-right input
– Leftmost derivation
– 1 symbol of look-ahead
• LR(1) parsers
– Left-to-right input
– Rightmost derivation
– 1 symbol of look-ahead
• Also: LL(k), LR(k), SLR, LALR, …
Grammars that this
can handle are
called LL(1)
grammars
Grammars that this
can handle are
called LR(1)
grammars

28. Parsing Restriction
• In a compiler’s parser, we don’t have long-distance
vision. We are usually limited to just one-symbol of
lookahead. The lookahead symbol is the next symbol
coming up in the input.
• Another restruction to parsing would be to implement
backtracking.
28

29. Top Down Predictive Parsing
• A predictive parser is characterized by its ability to
choose the production to apply solely on the basis of
the next input symbol and the current nonterminal
being processed.
• To enable this, the grammar must take a particular
form. We call such a grammar LL(1).
• The first "L" means we scan the input from left to right;
the second "L" means we create a leftmost derivation;
and the 1 means one input symbol of lookahead.
29

30. 30
Top-Down Parsing
• Start with the root of the parse tree
– Root of the tree: node labeled with the start symbol
• Algorithm:
Repeat until the fringe of the parse tree matches input string
– At a node A, select a production for A
Add a child node for each symbol on rhs
– If a terminal symbol is added that doesn’t match, backtrack
– Find the next node to be expanded (a non-terminal)
• Done when:
– Leaves of parse tree match input string (success)
– All productions exhausted in backtracking (failure)

31. Recursive Descent
• The first technique for implementing a predictive
parser is called recursive-descent.
• A recursive-descent parser consists of several small
functions, one for each nonterminal in the grammar.
• As we parse a sentence, we call the functions that
correspond to the left side nonterminal of the
productions we are applying. If these productions are
recursive, end up calling the functions recursively.
31

32. void a() {
choose an A-production, A  X1X2X3…Xn;
for (i = 1 to k) {
if (Xi is a non-terminal)
call procedure Xi();
else if (Xi equals the current input symbol a)
advance the input to the next symbol;
else /* an error has occurred*/
}
}
Recursive Descent
32

33. 33
Example
• Expression grammar
• Input string x – 2 * y
# Production rule
1
2
3
4
5
6
7
8
expr → expr + term
| expr - term
| term
term → term * factor
| term / factor
| factor
factor → number
| identifier

34. 34
Example
Rule Sentential form Input string
- expr expr
expr
x
+
term
fact
term
2 expr + term  x - 2 * y
3 term + term  x – 2 * y
6 factor + term  x – 2 * y
8 <id> + term x  – 2 * y
- <id,x> + term x  – 2 * y
 x - 2 * y
Current position in
the input stream

35. 35
Backtracking
Rule Sentential form Input string
- expr
2 expr + term  x - 2 * y
3 term + term  x – 2 * y
6 factor + term  x – 2 * y
8 <id> + term x  – 2 * y
? <id,x> + term x  – 2 * y
 x - 2 * y
Undo all these
productions

36. 36
Retrying
Rule Sentential form Input string
- expr
expr
expr
x
-
term
fact
term
2 expr - term  x - 2 * y
3 term - term  x – 2 * y
6 factor - term  x – 2 * y
8 <id> - term x  – 2 * y
- <id,x> - term x –  2 * y
 x - 2 * y
3 <id,x> - factor x –  2 * y
7 <id,x> - <num> x – 2  * y
fact
2

37. 37
Successful Parse
• All terminals match – we’re finished
Rule Sentential form Input string
- expr
expr
expr
x
-
term
fact
term
2 expr - term  x - 2 * y
3 term - term  x – 2 * y
6 factor - term  x – 2 * y
8 <id> - term x  – 2 * y
- <id,x> - term x –  2 * y
 x - 2 * y
4 <id,x> - term * fact x –  2 * y
6 <id,x> - fact * fact x –  2 * y
2
7 <id,x> - <num> * fact x – 2  * y
fact
- <id,x> - <num,2> * fact x – 2 *  y
8 <id,x> - <num,2> * <id> x – 2 * y 
term * fact
y

38. 38
Other Possible Parses
Rule Sentential form Input string
- expr
2 expr + term  x - 2 * y
2 expr + term + term  x – 2 * y
2 expr + term + term + term  x – 2 * y
2 expr + term + term + term + term  x – 2 * y
 x - 2 * y

39. 39
Left Recursion
• Formally,
A grammar is left recursive if  a non-terminal A such that A →* A a (for some set of
symbols a)
• Bad news:
Top-down parsers cannot handle left recursion
• Good news:
We can systematically eliminate left recursion
What does →* mean?
A → B x
B → A y

40. 40
Removing Left Recursion
• Two cases of left recursion:
• Transform as follows:
# Production rule
1
2
3
expr → expr + term
| expr - term
| term
# Production rule
4
5
6
term → term * factor
| term / factor
| factor
# Production rule
1
2
3
4
expr → term expr2
expr2 → + term expr2
| - term expr2
| e
# Production rule
4
5
6
term → factor term2
term2 → * factor term2
| / factor term2
| e

41. 41
Right-Recursive Grammar
• We can choose the right production by looking at
the next input symbol
– This is called lookahead
– BUT, this can be tricky…
# Production rule
1
2
3
4
5
6
7
8
9
10
expr → term expr2
expr2 → + term expr2
| - term expr2
| e
term → factor term2
term2 → * factor term2
| / factor term2
| e
factor → number
| identifier
Two productions
with no choice at all
All other productions are
uniquely identified by a
terminal symbol at the
start of RHS

42. Context-Free Languages
The inclusion hierarchy for
context-free languages
Context-free languages
Deterministic languages (LR(k))
LL(k) languages Simple precedence
languages
LL(1) languages Operator precedence
languages
LR(k) ≡ LR(1)

43. Context-Free Grammars
• Operator precedence
includes some ambiguous
grammars
• LL(1) is a subset of SLR(1)
The inclusion hierarchy for
context-free grammars
Context-free grammars
Floyd-Evans
Parsable
Unambiguous
CFGs
Operator
Precedence
LR(k)
LR(1)
LALR(1)
SLR(1)
LR(0)
LL(1)
LL(k)

44. Beyond Syntax
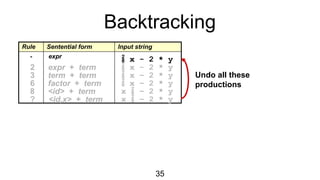
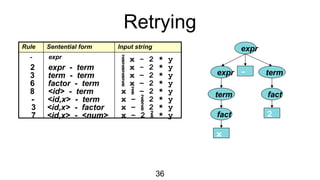
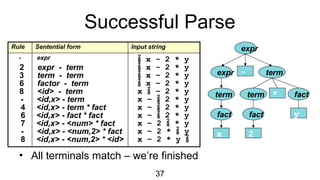
• There is a level of correctness that is deeper than grammar
fie(a,b,c,d)
int a, b, c, d;
{ … }
fee() {
int f[3],g[0],
h, i, j, k;
char *p;
fie(h,i,“ab”,j, k);
k = f * i + j;
h = g[17];
printf(“<%s,%s>.n”,
p,q);
p = 10;
}
What is wrong with this program?
(let me count the ways …)

45. Semantics
• There is a level of correctness that is deeper than grammar
fie(a,b,c,d)
int a, b, c, d;
{ … }
fee() {
int f[3],g[0],
h, i, j, k;
char *p;
fie(h,i,“ab”,j, k);
k = f * i + j;
h = g[17];
printf(“<%s,%s>.n”,
p,q);
p = 10;
}
What is wrong with this program?
(let me count the ways …)
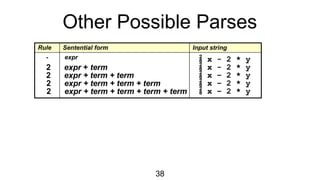
• declared g[0], used g[17]
• wrong number of args to fie()
• “ab” is not an int
• wrong dimension on use of f
• undeclared variable q
• 10 is not a character string
All of these are “deeper than
syntax”

46. Syntax-directed translation
• In syntax-directed translation, we attach ATTRIBUTES to grammar symbols.
• The values of the attributes are computed by SEMANTIC RULES associated with
grammar productions.
• Conceptually, we have the following flow:
• In practice, however, we do everything in a single pass.

47. Syntax-directed translation
• There are two ways to represent the semantic rules we associate with
grammar symbols.
– SYNTAX-DIRECTED DEFINITIONS (SDDs) do not specify the order in which
semantic actions should be executed
– TRANSLATION SCHEMES explicitly specify the ordering of the semantic
actions.
• SDDs are higher level; translation schemes are closer to
• an implementation

48. Syntax-directed definitions
• The SYNTAX-DIRECTED DEFINITION (SDD) is a generalization of
the context-free grammar.
• Each grammar symbol in the CFG is given a set of ATTRIBUTES.
• Attributes can be any type (string, number, memory loc, etc)
• SYNTHESIZED attributes are computed from the values of the
CHILDREN of a node in the parse tree.
• INHERITED attributes are computed from the attributes of the
parents and/or siblings of a node in the parse tree.

49. Attribute dependencies
• Given a SDD, we can describe the dependencies between the
attributes with a DEPENDENCY GRAPH.
• A parse tree annotated with attributes is called an ANNOTATED
parse tree.
• Computing the attributes of the nodes in a parse tree is called
ANNOTATING or DECORATING the tree.

50. Form of a syntax-directed
definition
• In a SDD, each grammar production A -> α has associated with it
semantic rules
• b := f( c1, c2, …, ck )
• where f() is a function, and either
1. b is a synthesized attribute of A, and c1, c2, …, are attributes of the
grammar symbols of α, or
2. b is an inherited attribute of one of the symbols on the RHS, and c1, c2, …
are attributes of the grammar symbols of α
• in either case, we say b DEPENDS on c1, c2, …, ck.

51. Semantic rules
• Usually we actually write the semantic rules with expressions
instead of functions.
• If the rule has a SIDE EFFECT, e.g. updating the symbol table, we
write the rule as a procedure call.
• When a SDD has no side effects, we call it an ATTRIBUTE
GRAMMAR.

52. Synthesized attributes
• Synthesized attributes depend only on the attributes of
• children. They are the most common attribute type.
• If a SDD has synthesized attributes ONLY, it is called a S-ATTRIBUTED DEFINITION.
• S-attributed definitions are convenient since the
attributes can be calculated in a bottom-up
traversal of the parse tree.

53. Example SDD: desk calculator
• Production Semantic Rule
• L -> E newline print( E.val )
• E -> E1 + T E.val := E1.val + T.val
• E -> T E.val := T.val
• T -> T1 * F T.val := T1.val x F.val
• T -> F T.val := F.val
• F -> ( E ) F.val := E.val
• F -> number F.val := number.lexval
• Notice the similarity to the yacc spec from last lecture.

54. Calculating synthesized attributes
Input string: 3*5+4 newline
Annotated tree:

55. Inherited attributes
• An inherited attribute is defined in terms of the
attributes of the node’s parents and/or siblings.
• Inherited attributes are often used in compilers for passing contextual
information forward, for example, the type keyword in a variable declaration
statement.

56. Example SDD with an inherited attribute
• Suppose we want to describe decls like “real x, y, z”
• Production Semantic Rules
• D -> T L L.in := T.type
• T -> int T.type := integer
• T -> real T.type := real
• L -> L1, id L1.in := L.in
• addtype( id.entry, L.in )
• L -> id addtype( id.entry, L.in )
• L.in is inherited since it depends on a sibling or parent.
addtype() is just
a procedure that
sets the type
field in the
symbol table.

57. Annotated parse tree for real id1, id2, id3
What are the
dependencies?

58. Dependency graphs
• If an attribute b depends on attribute c, then attribute b has to be
evaluated AFTER c.
• DEPENDENCY GRAPHS visualize these requirements.
– Each attribute is a node
– We add edges from the node for attribute c to the node for attribute b, if
b depends on c.
– For procedure calls, we introduce a dummy synthesized attribute that
depends on the parameters of the procedure calls.

59. Dependency graph example
• Production Semantic Rule
• E -> E1 + E2 E.val := E1.val + E2.val
• Wherever this rule appears in the parse, tree we draw:

60. Example dependency graph

61. Example dependency graph

62. Finding a valid evaluation order
• A TOPOLOGICAL SORT of a directed acyclic graph orders the
nodes so that for any nodes a and b such that a -> b, a appears
BEFORE b in the ordering.
• There are many possible topological orderings for a DAG.
• Each of the possible orderings gives a valid order for evaluation of
the semantic rules.

63. Example dependency graph