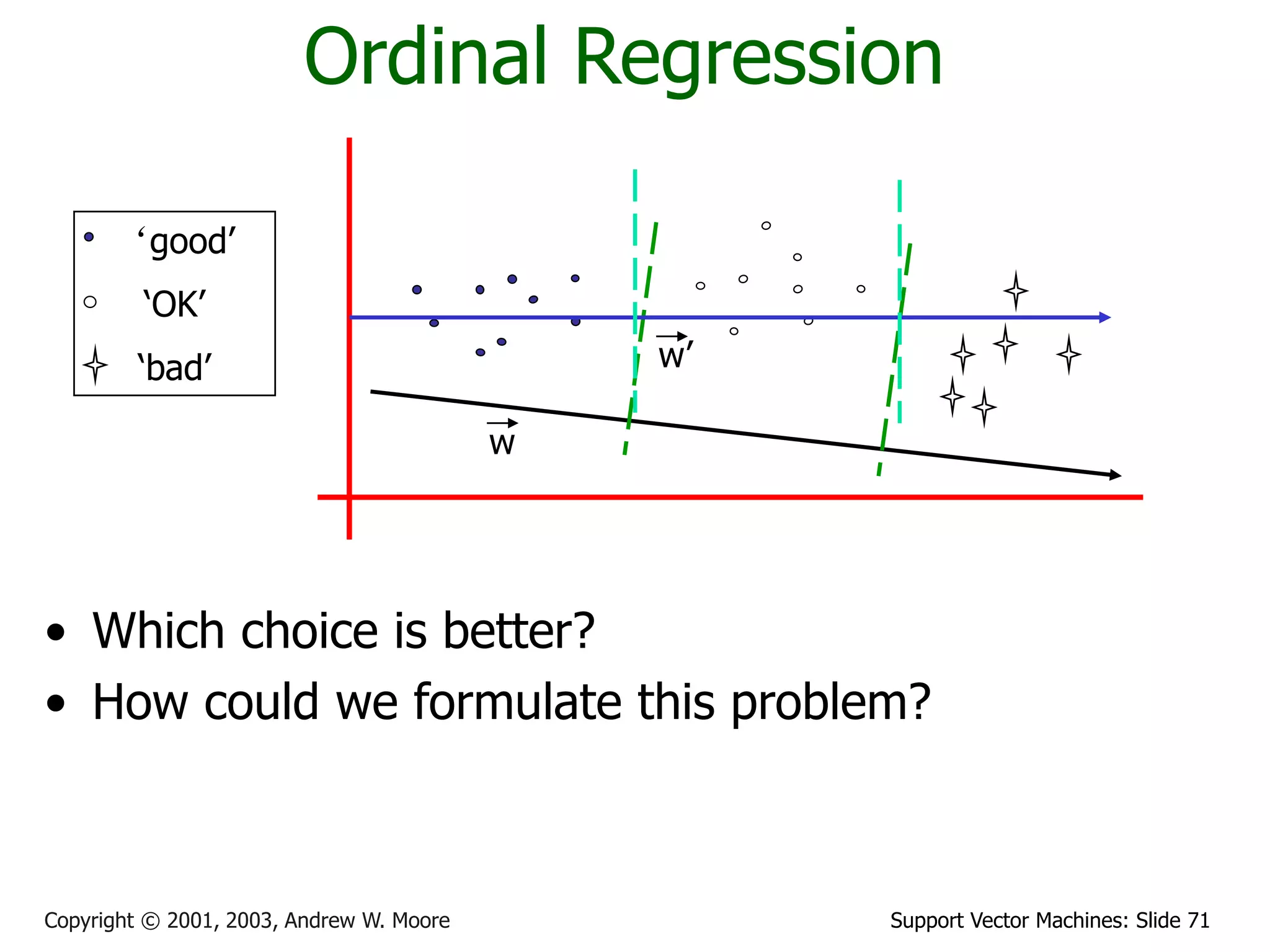
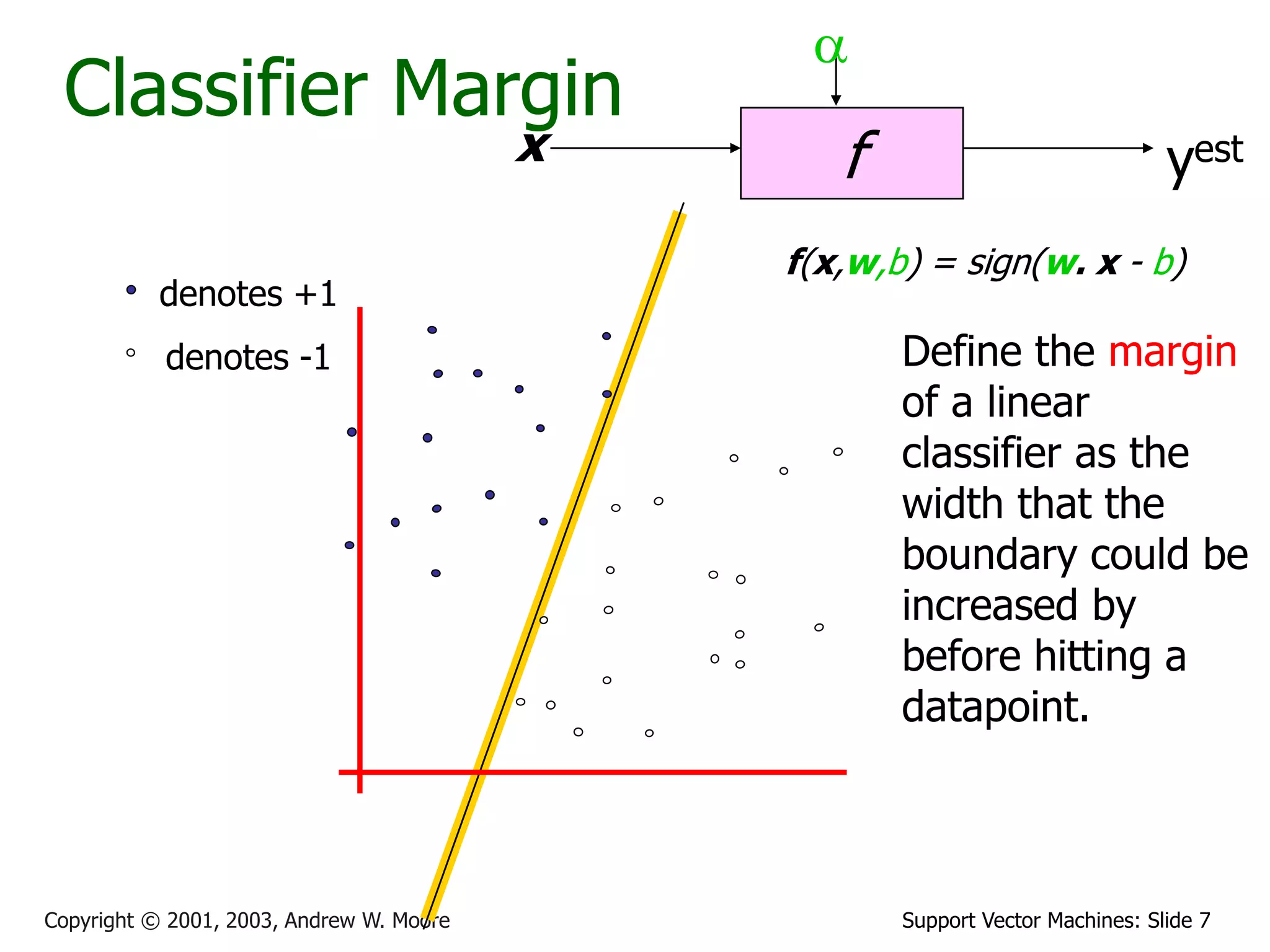
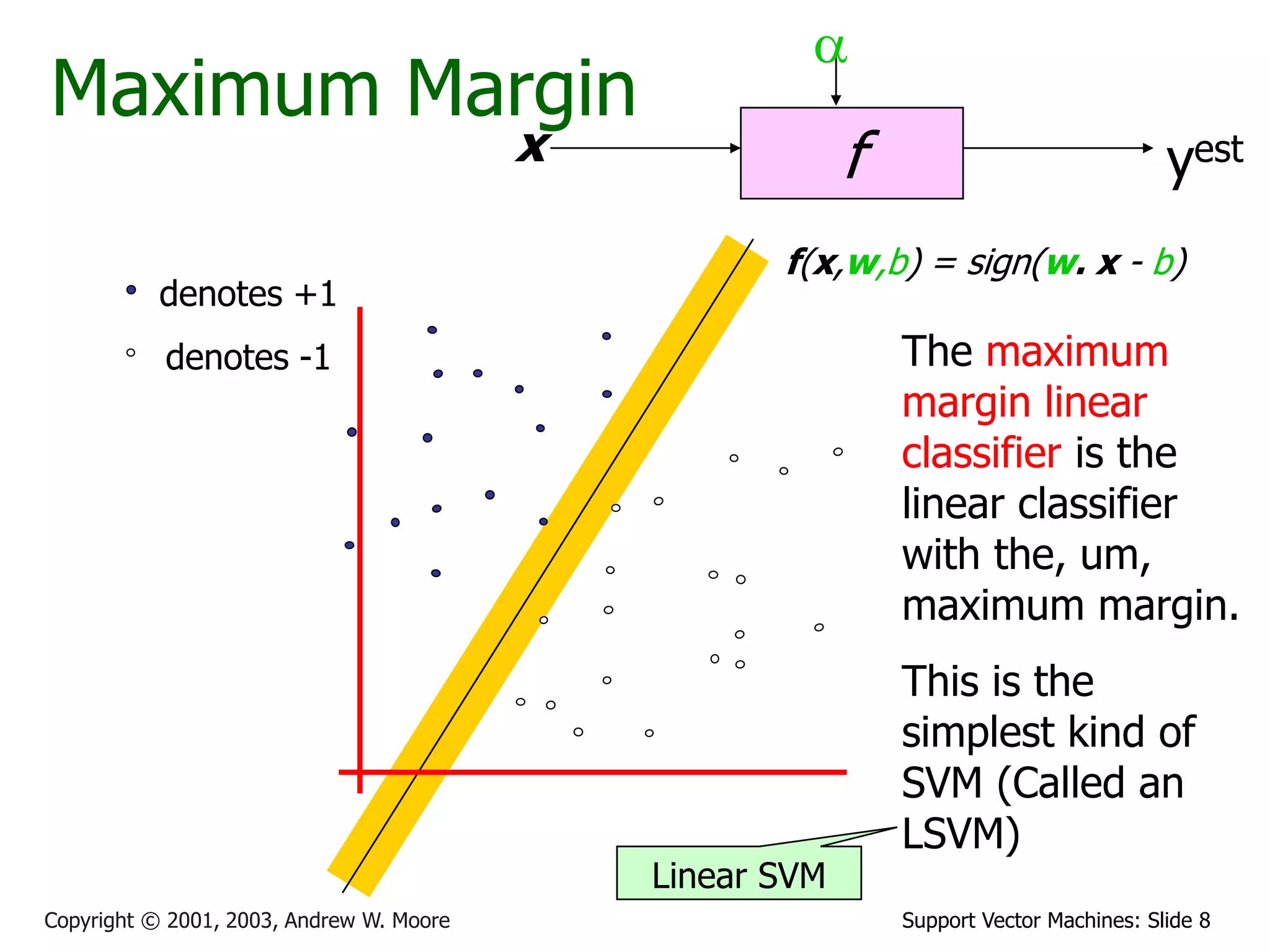
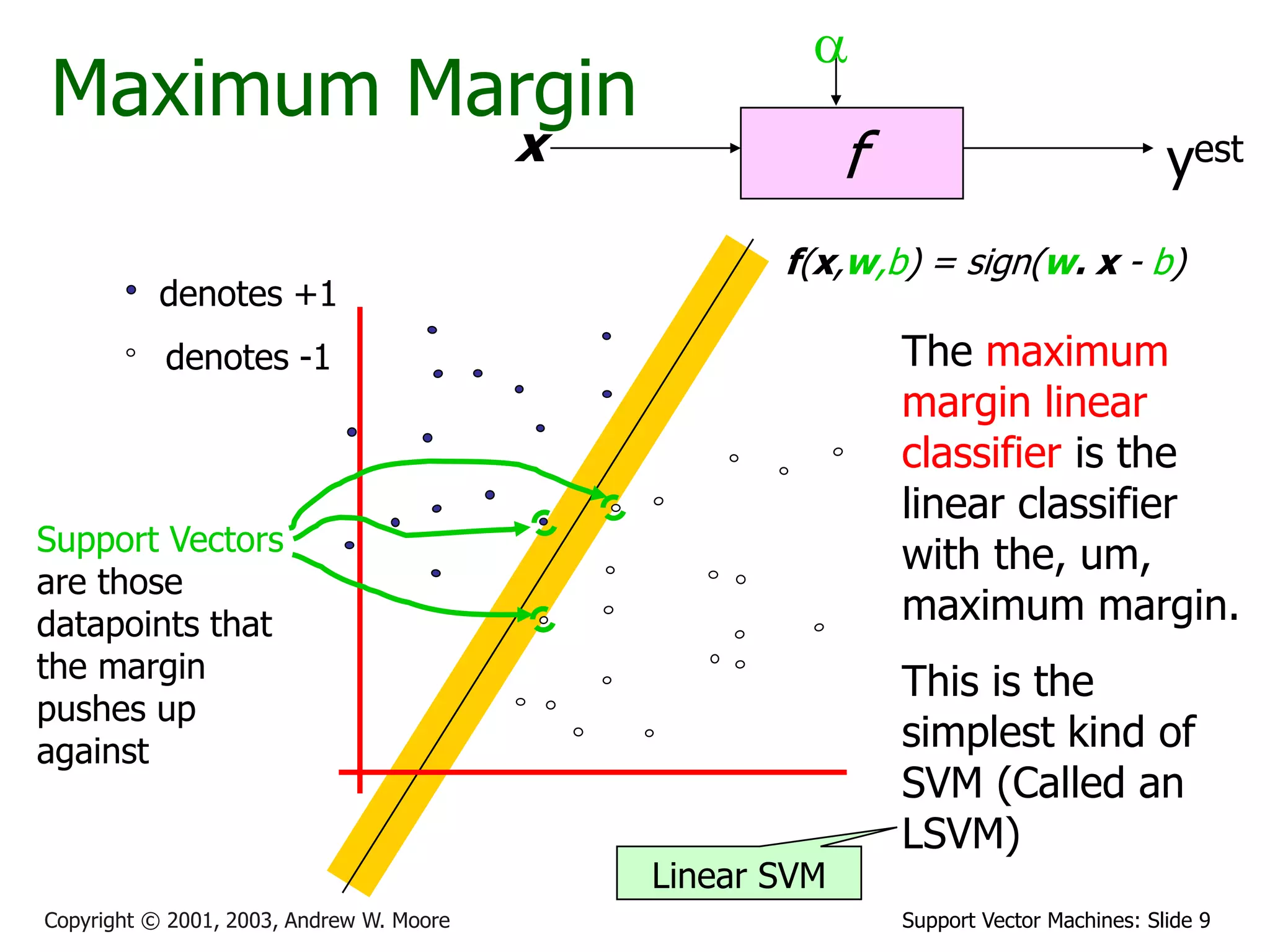
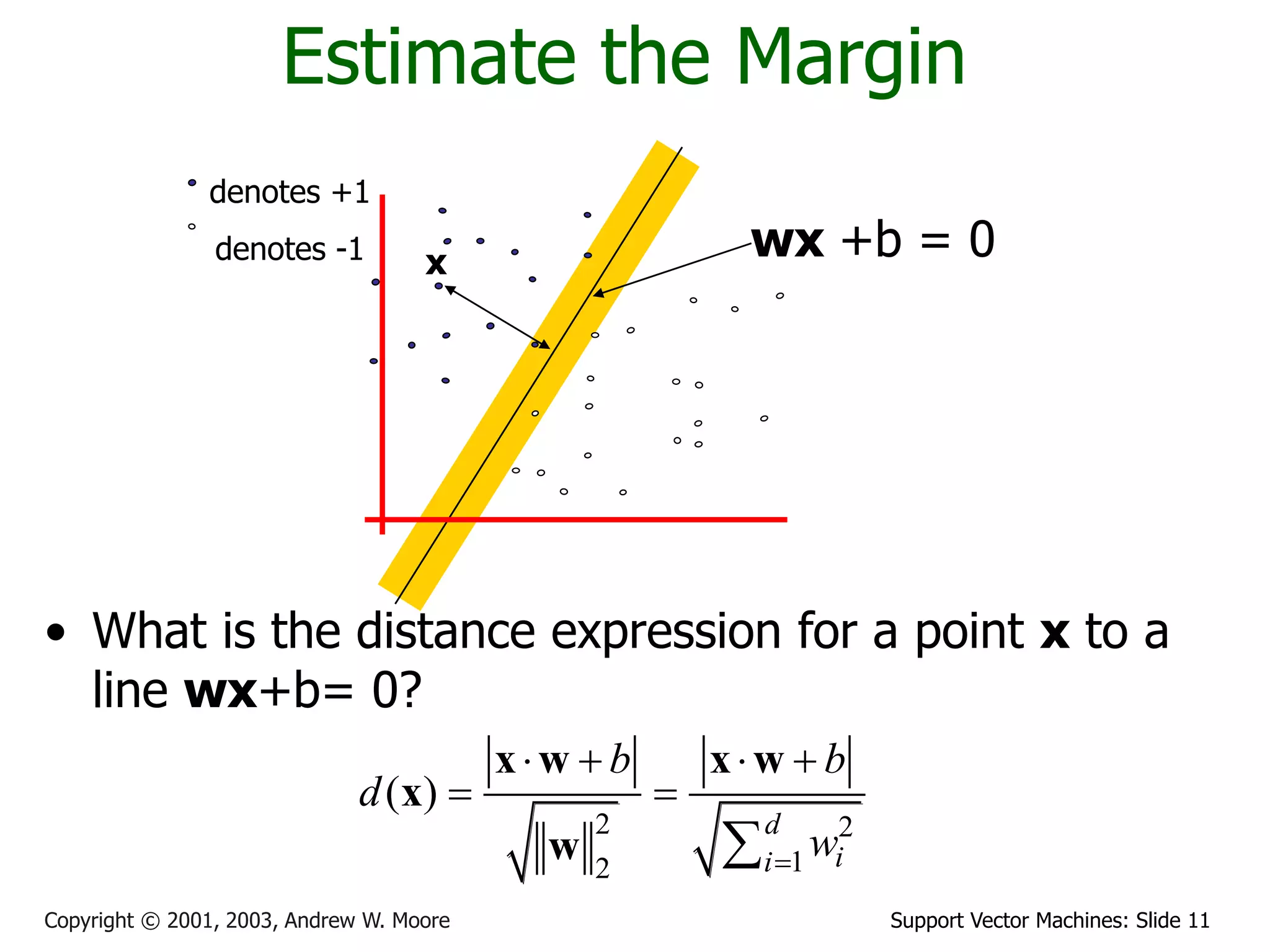
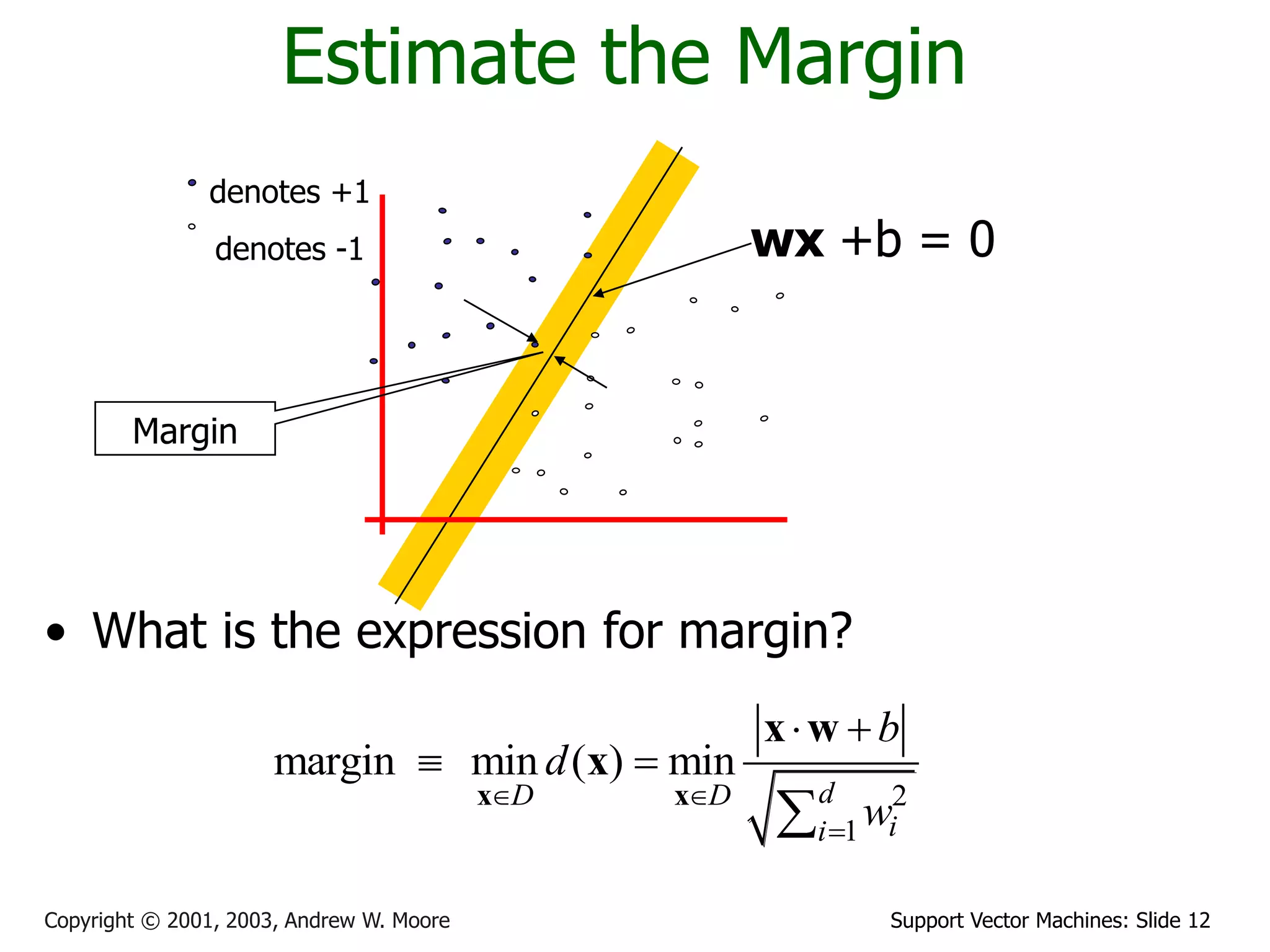
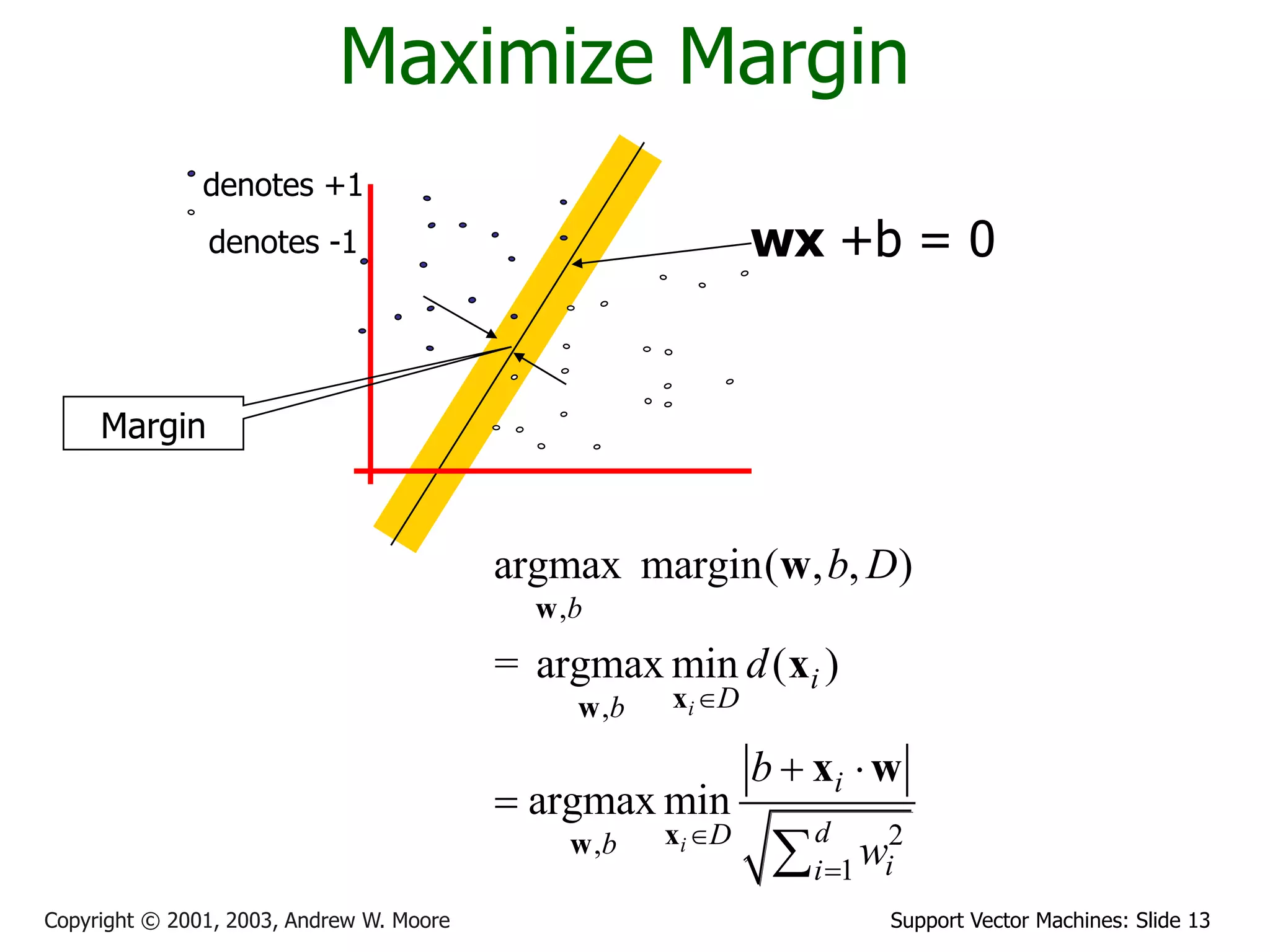
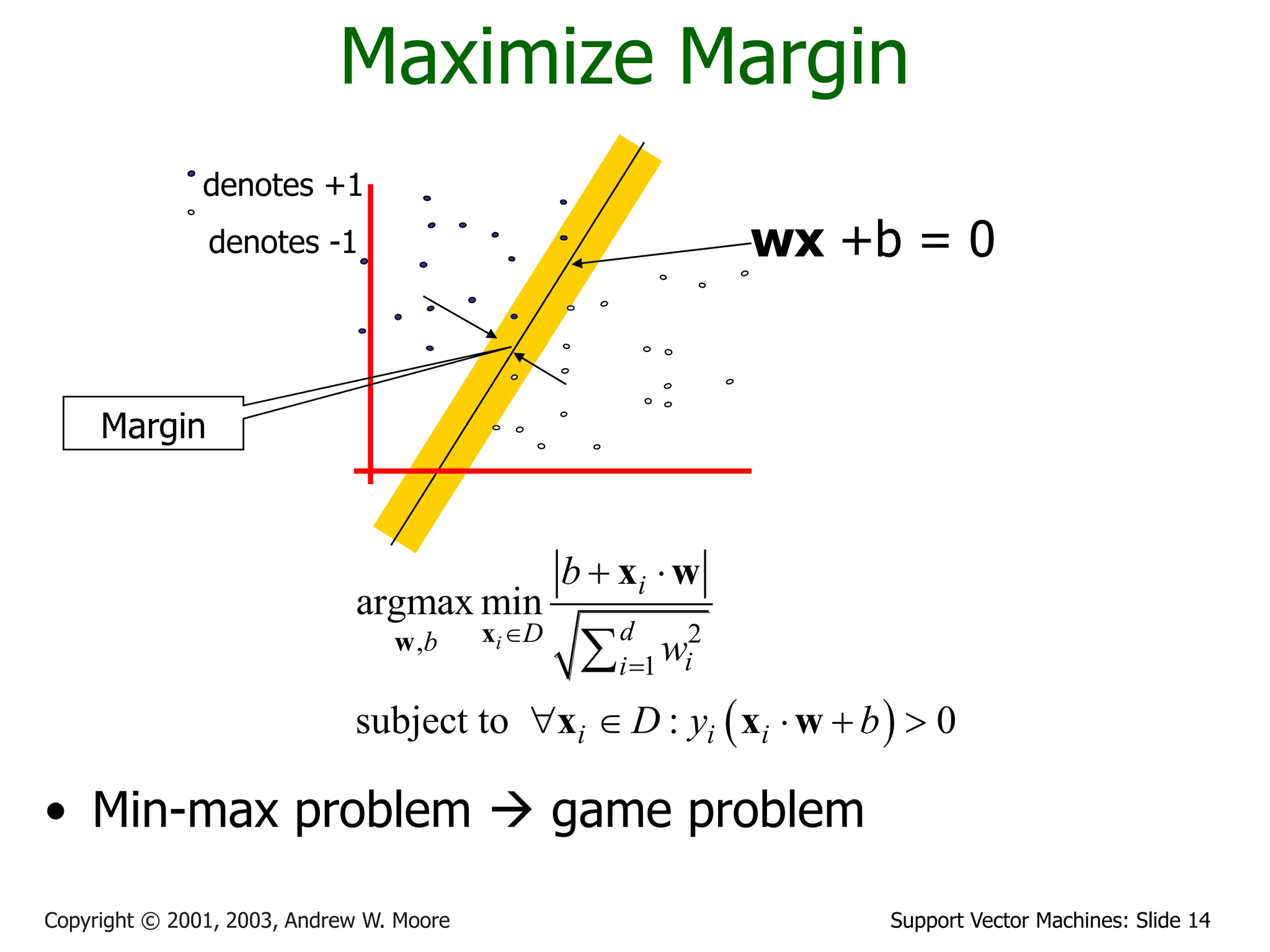
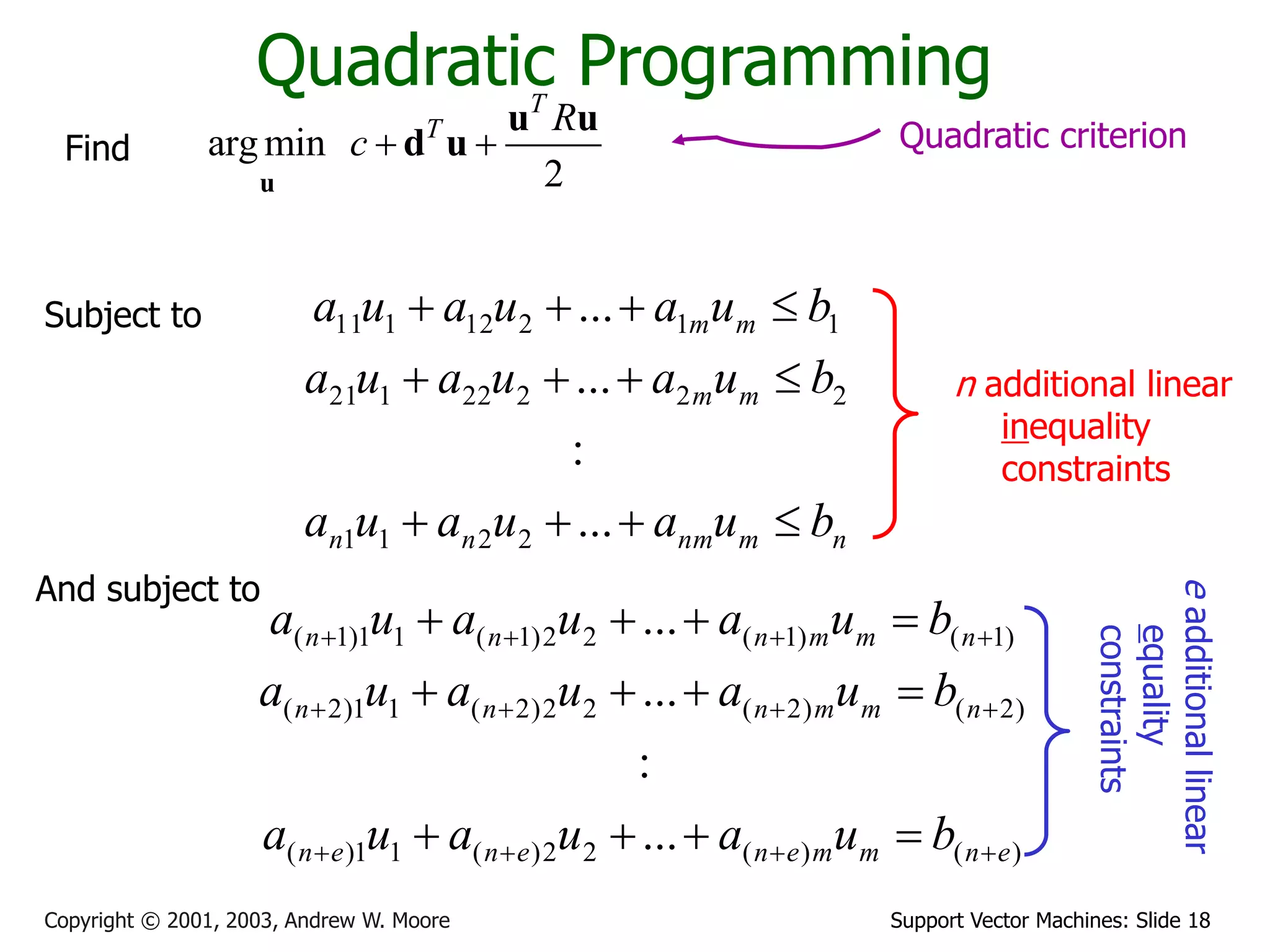
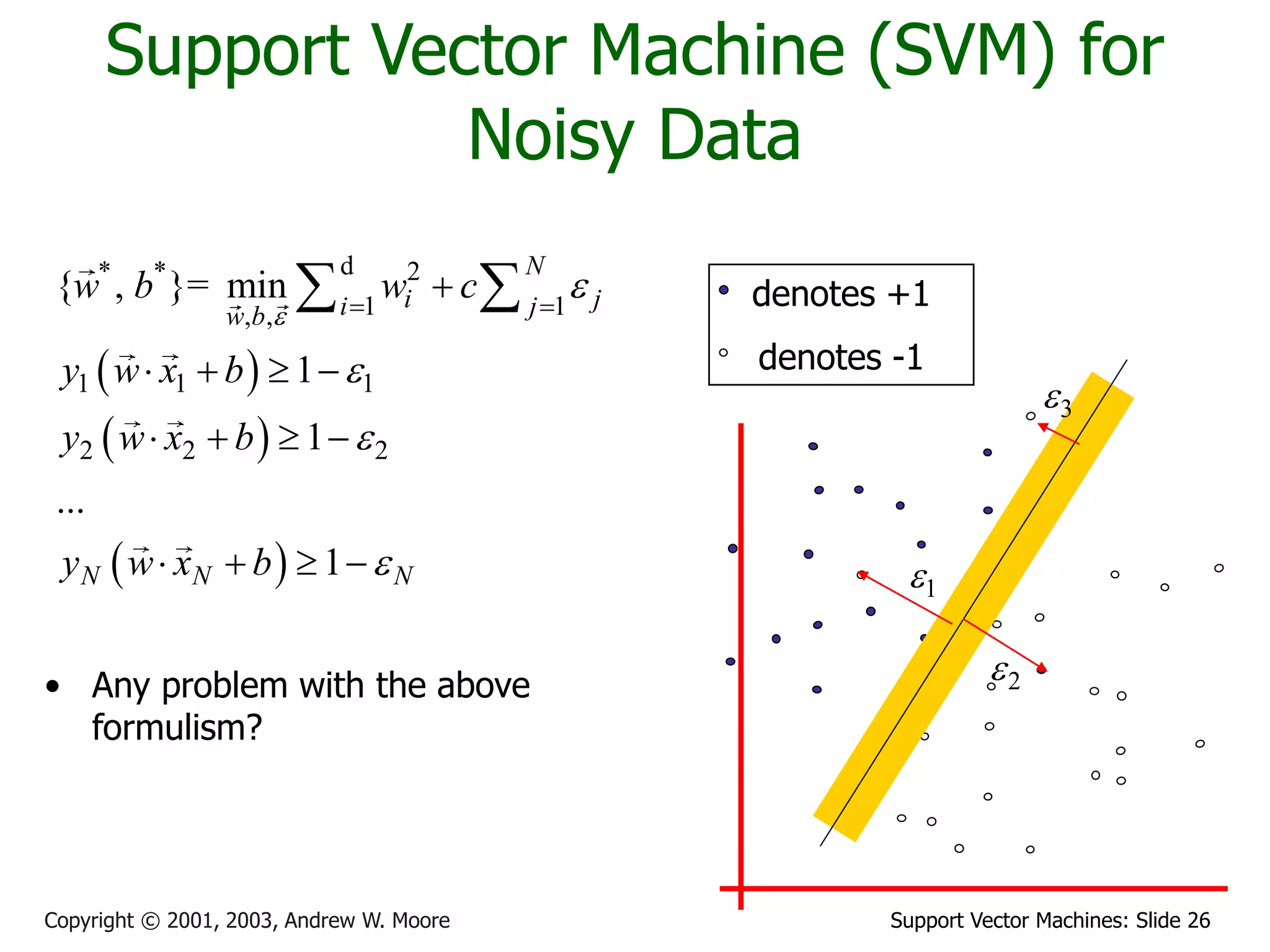
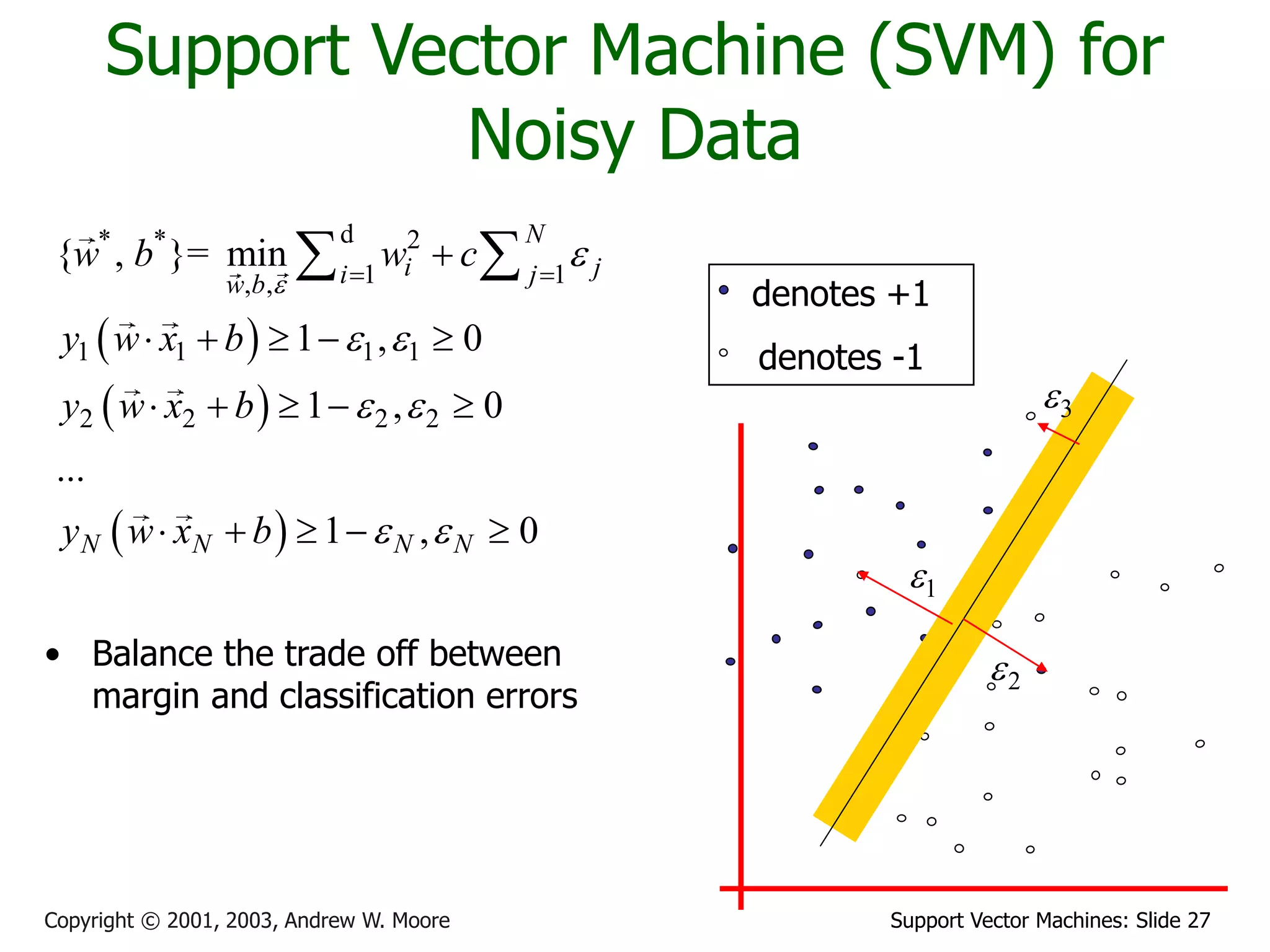
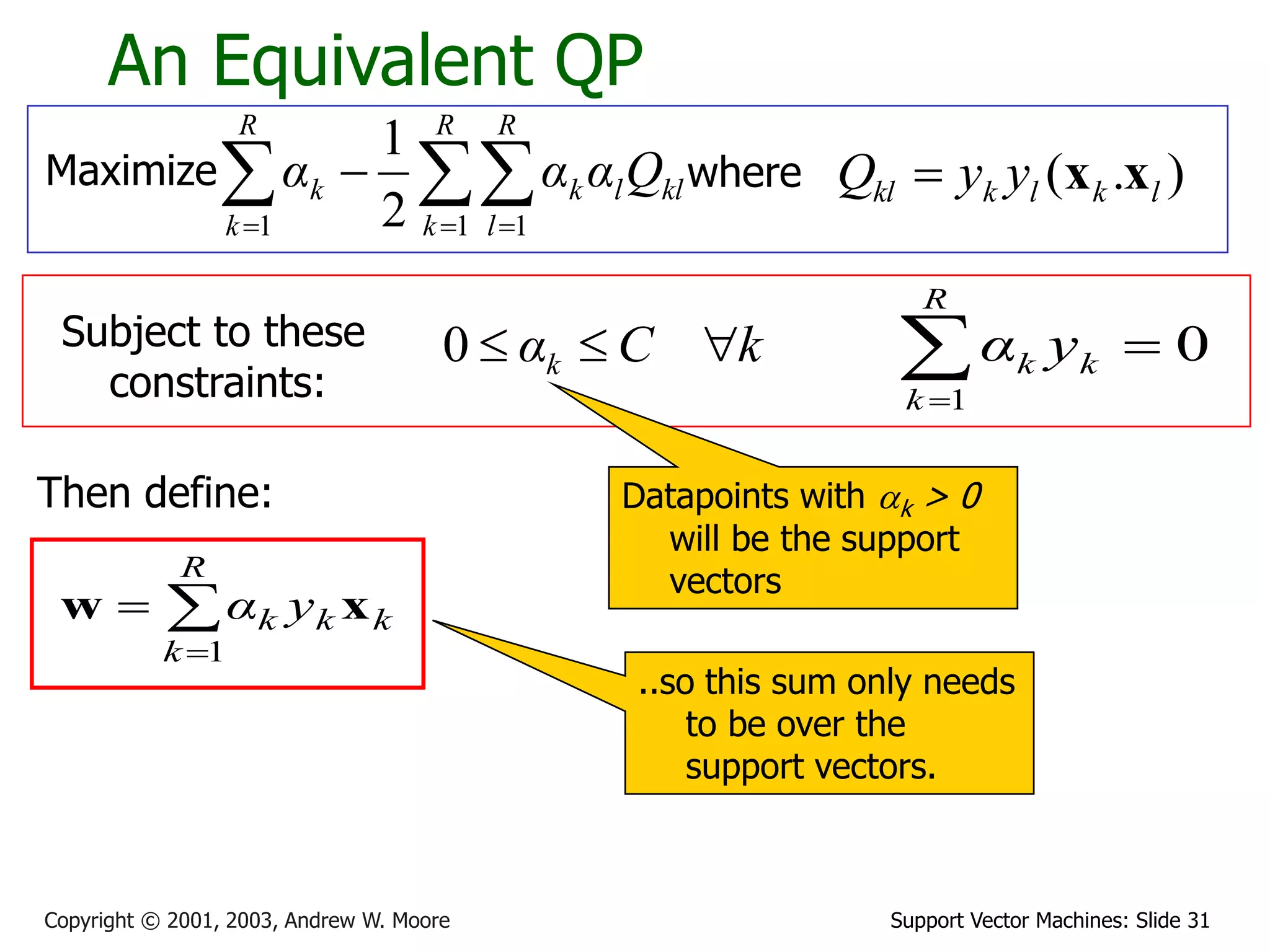
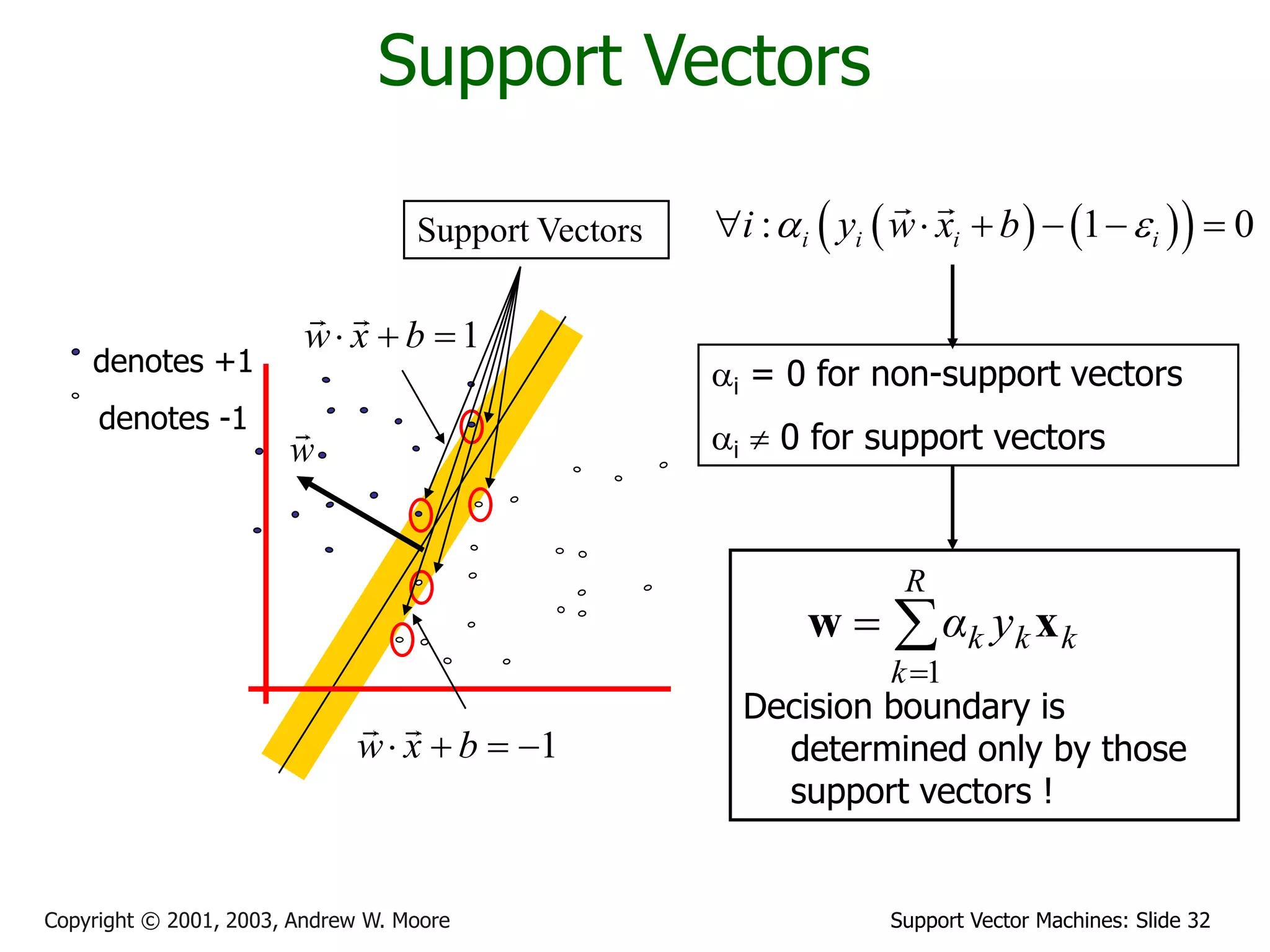
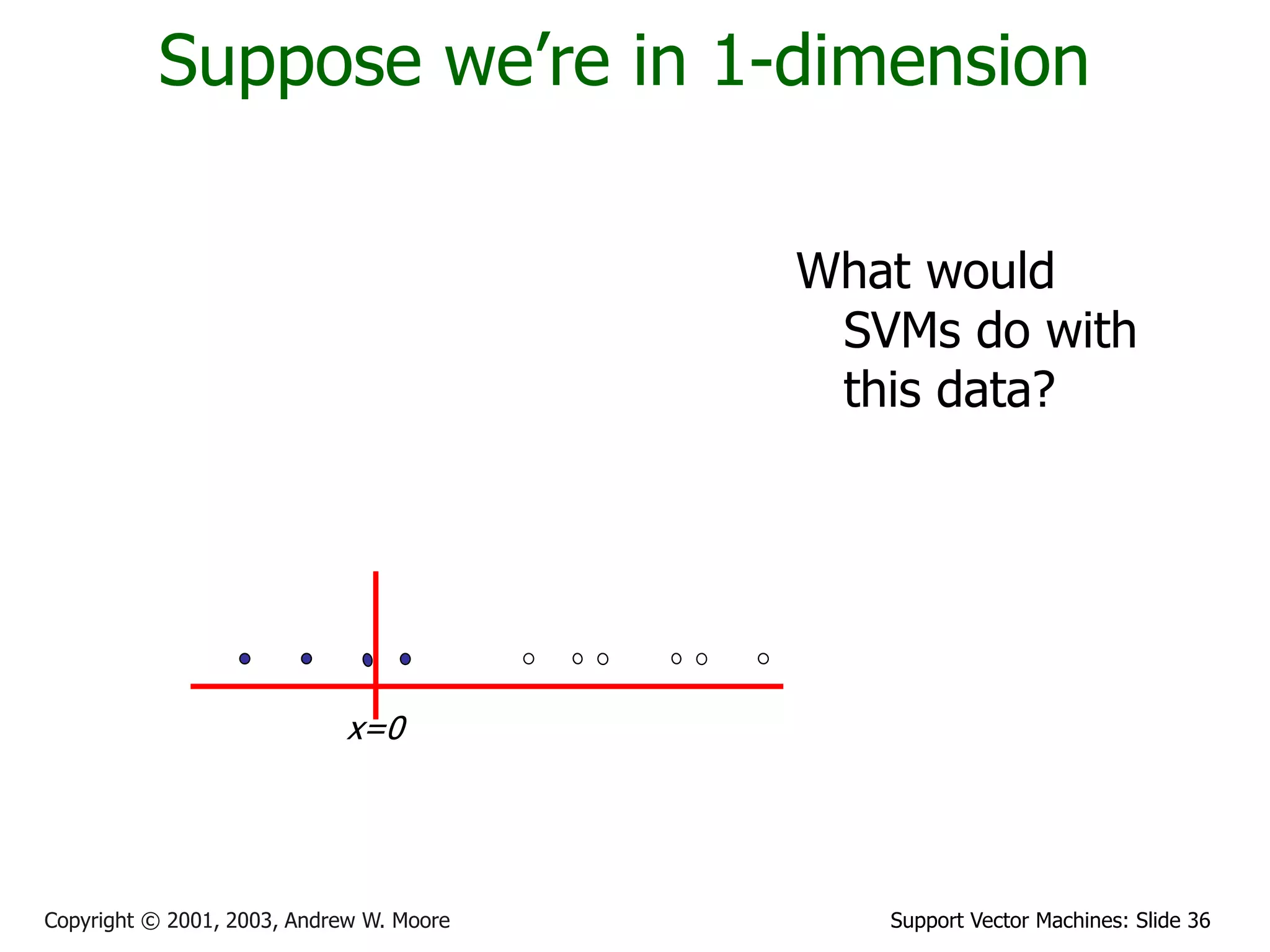
The document discusses support vector machines (SVMs) for classification. It introduces linear classifiers and maximum margin classifiers. A maximum margin classifier finds the linear decision boundary that maximizes the margin or distance between the boundary and the closest data points of each class. These closest data points are called the support vectors. Finding the maximum margin classifier can be formulated as a quadratic programming optimization problem that aims to minimize a quadratic function subject to linear constraints. The document provides slides explaining these concepts from an SVM tutorial.























![Support Vector Machines: Slide 41
Copyright © 2001, 2003, Andrew W. Moore
Common SVM basis functions
zk = ( polynomial terms of xk of degree 1 to q )
zk = ( radial basis functions of xk )
zk = ( sigmoid functions of xk )
This is sensible.
Is that the end of the story?
No…there’s one more trick!
2
2
|
|
exp
)
(
]
[
j
k
k
j
k φ
j
c
x
x
z](https://image.slidesharecdn.com/svm-jain-230316121042-f3c88c7b/75/svm-jain-ppt-41-2048.jpg)