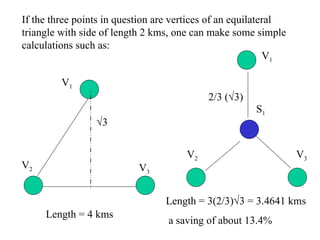
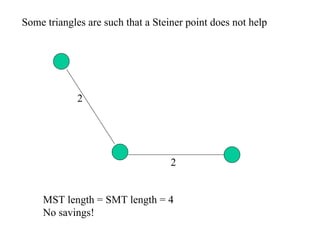
The document discusses Steiner trees, which are trees that connect a set of points while allowing additional intermediate points called Steiner points. Some key points: 1) Adding Steiner points can significantly reduce the total length needed to connect points compared to just connecting the points directly. For example, adding one Steiner point to connect three points in a triangle can reduce the length by over 13%. 2) Steiner trees have applications in areas like circuit board design where they help minimize the total wiring or pathway length needed. 3) Finding optimal Steiner trees is computationally difficult, so heuristics like depth-first search are often used to find approximate solutions, especially for larger point sets.

1. Steiner Tree Applications Presented by T. N. Badri

2. The Steiner problem dates back to Pierre Fermat. Even Napolean has worked on this problem. Consider three points V 1 , V 2 , and V 3 . The shortest network interconnecting these three points is the sum of the two shortest sides of the triangle. If one includes a fourth point S 1 in the plane of the triangle, one can find a much shorter interconnecting network. V 1 V 2 V 3 V 1 V 2 V 3 S 1

3. If the three points in question are vertices of an equilateral triangle with side of length 2 kms, one can make some simple calculations such as: Length = 4 kms 2/3 (  3) Length = 3(2/3)  3 = 3.4641 kms a saving of about 13.4%  3 V 1 V 2 V 3 V 1 V 2 V 3 S 1

4. If it costs about Rs. 3 lakhs to lay one km of road this is a saving of 0.134 * 300,000 * 4 = Rs. 160,800 on an initial total cost of Rs. 12 lakhs.

5. Steiner points have some properties Exactly three edges meet at every Steiner vertex. The angles between the edges meeting at a Steiner vertex is 120 degrees. If there are N vertices then we can use a maximum of N-2 Steiner vertices.

6. MST length = 1 +  3 SMT length is 2.6458 A saving of 3.1588% 1  3 2 (-0.2857, 0.2474)

7. Some triangles are such that a Steiner point does not help 2 2 MST length = SMT length = 4 No savings!

8. Geometric Construction using compass and straight edge

9. Four terminal sites in 3d with one Steiner point Four terminal sites in 3d with two Steiner points

10. Steiner trees with the rectilinear metric appear when laying down conductive pathways on a printed circuit board.

11. HANAN GRID

12. Development of Path Topology in 2d (Counter-clockwise from top right)

13. Planar-Sausage with 8 terminal sites Conjectured infinite 2d structure with best Steiner Ratio  3/2

14. Planar-Sausage with 9 terminal sites Conjectured infinite 2d structure with best Steiner Ratio  3/2

15. Planar-Sausage with 10 terminal sites Conjectured 2d structure with best Steiner Ratio  3/2

16. Planar-Sausage with 11 terminal sites Conjectured infinite 2d structure with best Steiner Ratio =  3/2

17. Steiner Ratio in 2d falls to  3/2 as the number of terminal sites increase

18. R-Sausage Minimum Spanning Tree

19. R-Sausage Conjectured infinite 3d structure with best Steiner Ratio

20. Another view of 3d sausage Minimum Spanning Tree Steiner Minimal Tree

21. Steiner Ratio in 3d falls to  0.784 as the number of terminal sites increase

22. Four types of Steiner points - according to neighbouring vertices

23. R-Sausage structure is preserved under composition. It is a semi-group.

24. Topology for Even and Odd Sized R-Sausages in 3d

25. d1 d2 d3 (x2,y2) (x1, y1) (x3,y3) (x,y) The average of the vertex coordinates weighted by their reciprocal distances from the Steiner point.

26. Depth First Search of point set Heuristic for large point set

27. Depth First Search of point set – The first Steiner point Heuristic for large point set

28. Depth First Search of point set – The second Steiner point Heuristic for large point set

29. Depth First Search of point set – The third Steiner point Heuristic for large point set

30. Depth First Search of point set – The fourth Steiner point Heuristic for large point set

31. Depth First Search of point set – Return to root node Heuristic for large point set

32. Depth First Search of point set – First Steiner vertex Heuristic for large point set

33. Depth First Search of point set – Second Steiner vertex Heuristic for large point set

34. Depth First Search of point set – Third Steiner vertex Heuristic for large point set

35. Depth First Search of point set – Fourth Steiner vertex Heuristic for large point set

36. Depth First Search of point set – Fifth Steiner vertex Heuristic for large point set

37. Steiner Tree and Minimum Spanning Tree for a small random point set in unit cube Minimal Interconnecting Tree for data without any structure

38. Steiner Tree and Minimum Spanning Tree for a medium sized random point set in unit cube Minimal Interconnecting Tree for data without any structure

39. Steiner Tree and Minimum Spanning Tree for Hundred random points in unit cube Minimal Interconnecting Tree for data without any structure

40. Steiner Tree and Minimum Spanning Tree for 500 random points in unit cube Minimal Interconnecting Tree for data without any structure

41. Amino Acid Sequence of a Protein (Lysozyme)

42. Network of Amide Planes in a Protein

43. Three Dimensional Structure of Two Amide Planes

44. THANK YOU