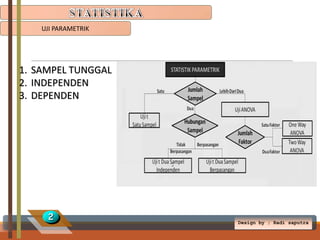
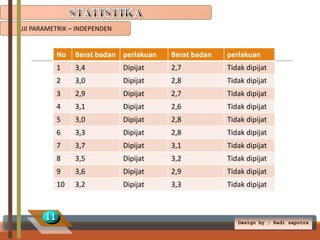
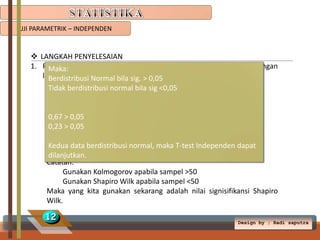
Dokumen tersebut membahas tentang uji parametrik pada statistika, termasuk uji parametrik untuk sampel tunggal, independen, dan dependen. Uji parametrik digunakan untuk menguji hipotesis dengan asumsi bahwa data berasal dari populasi normal. Dokumen ini memberikan contoh-contoh soal dan langkah penyelesaiannya menggunakan uji t satu sampel, uji t independen, dan uji t dependen.

1. STATISTIKA
1
Design by ; Radi saputra

2. UJI PARAMETRIK
1. SAMPEL TUNGGAL
2. INDEPENDEN
3. DEPENDEN
2
Design by ; Radi saputra

3. UJI PARAMETRIK – SAMPEL TUNGGAL
 Kapan menggunakan uji parametrik sampel tunggal????
digunakan ketika ingin menguji suatu nilai rata-rata dari satu
sampel, dengan dibandingkan dengan rata-rata sekelompok sampel-sampel
lainnya. Atau untuk mengetahui apakah sampel tersebut berasal dari populasi
tertentu, sementara tidak ada informasi mengenai populasi sampel
tersebut, sehingga perlu dibandingkan dengan sampel-sampel dari populasi
tertentu.
 Syarat penggunaan Uji t satu Sample :
1. Data harus berdistribusi normal
 Contoh :
seorang peneliti ingin menguji produktivitas Varietas baru dari satu
sampel lahan sawahnya, dengan dibandingkan dengan enam lahan sawah
disekitarnya yang menggunakan varietas lama. Apakah ada perbedaan secara
signifikan atau tidak.
3
Design by ; Radi saputra

4. UJI PARAMETRIK – SAMPEL TUNGGAL
Latihan :
seorang peneliti ingin menguji produktivitas Varietas baru dari satu
sampel lahan sawahnya, dengan dibandingkan dengan enam lahan sawah
disekitarnya yang menggunakan varietas lama. Apabila rata-rata produktifitas
varietas baru adalah 8ton/ha, dan rata-rata produktifitas 6 sawah disekitarnya
adalah
Lahan 1 = 5ton/ha
Lahan 2 = 7ton/ha
Lahan 3 = 6,5ton/ha
Lahan 4 = 7,5ton/ha
Lahan 5 = 7ton/ha
Lahan 6 = 6ton/ha
Jika taraf signifikan sebesar 5% Apakah ada perbedaan secara signifikan atau
tidak??
4
Design by ; Radi saputra

5. UJI PARAMETRIK – SAMPEL TUNGGAL
HIPOTESIS :
H0 : Produktifitas tanaman padi dari varietas baru = Produktifitas tanaman padi
dari varietas lama.
H1 : Produktifitas tanaman padi dari varietas baru ≠ Produktifitas tanaman padi
dari varietas lama.
Taraf signifikansi 5%
5
Design by ; Radi saputra

6. UJI PARAMETRIK – INDEPENDEN
 LANGKAH PENYELESAIAN
1. Penuhi syarat “data harus berdistribusi normal”. Test data dengan
Ketentuan:
langkah berikut:
Berdistribusi Normal bila sig. > 0,05
1. Klik analyze  Descriptive statistics  Expoler
Tidak berdistribusi normal bila sig <0,05
2. Berat badan dipindah ke Depedent list.
3. Perlakuan dipindah ke Factor list.
4. Klik Plots
0,607 > 0,05
5. Hilangkan centang Steam-and-leaf, dan centang Histogram.
6. Centang Normality plots with test. Klik Continue  OK
Maka data berdistribusi normal, sehingga One SampleT-test
dapat dilanjutkan.
Kemudian analisis pada table “Test of Normality”.
Catatan:
Gunakan Kolmogorov apabila sampel >50
Gunakan Shapiro Wilk apabila sampel <50
Maka yang kita gunakan sekarang adalah nilai signisifikansi Shapiro
Wilk.
6
Design by ; Radi saputra

7. UJI PARAMETRIK – DEPENDEN
 LANGKAH PENYELESAIAN
2. One Sample T-test
1. Klik Analyze  Compare means  One Sample T Test
2. Masukkan Produktifitas_lama ke Variable, dan Test Value isi dengan
rata-rata sampel yang di test.
3. Klik Options isi taraf kepercayaan 95% (didapat dari 100% dikurang
nilai signifikansi(5%))
4. Klik Continue  OK.
Kemudian analisislah pada table output.
7
Design by ; Radi saputra

8. UJI PARAMETRIK – SAMPEL TUNGGAL
Hipotesis:
H0 diterima : bila sig. > 0,05
H0 ditolak : bila sig. < 0,05 maka H1 diterima.
Maka
0,009 < 0,05
H0 ditolak dan H1 diterima
H1 : Produktifitas tanaman padi dari varietas baru ≠ Produktifitas
tanaman padi dari varietas lama.
HIPOTESIS
H0 : Produktifitas tanaman padi dari varietas baru = Produktifitas tanaman padi
dari varietas lama.
H1 : Produktifitas tanaman padi dari varietas baru ≠ Produktifitas tanaman padi
dari varietas lama.
8
Design by ; Radi saputra

9. UJI PARAMETRIK – INDEPENDEN
 Kapan menggunakan uji parametrik INDEPENDEN????
digunakan ketika menguji data Antara variable satu tidak saling
berkaitan atau INDEPENDEN.
 Syarat penggunaan INDEPENDEN
1. Data harus berdistribusi normal
2. Kedua sampelnya INDEPENDEN (tidak berhubungan)
 Contoh :
1. seorang ingin meneliti berat badan bayi yang diberi pemijatan akan
lebih baik dari pada bayi yang tidak diberi pemijatan
2. Seorang peneliti ingin mengetahui apakah berat badan sapi yang
diberikan jenis pakan A lebih baik dari yang diberi jenis pakan B.
9
Design by ; Radi saputra

10. UJI PARAMETRIK – INDEPENDEN
Latihan :
1. Seorang peneliti ingin mengetahui berat badan bayi yang diberi
pemijatan apakah lebih baik dari yang tidak dipijat. Datanya sebagai
berikut. Signisifikansi 5% (0,05).
HIPOTESIS
H0: berat badan bayi yang dipijat = berat badan bayi yang tidak dipijat.
H1: berat badan bayi yang dipijat ≠ berat badan bayi yang tidak dipijat.
10
Design by ; Radi saputra

11. UJI PARAMETRIK – INDEPENDEN
No
Berat badan
perlakuan
1
3,4
Dipijat
2,7
Tidak dipijat
2
3,0
Dipijat
2,8
Tidak dipijat
3
2,9
Dipijat
2,7
Tidak dipijat
4
3,1
Dipijat
2,6
Tidak dipijat
5
3,0
Dipijat
2,8
Tidak dipijat
6
3,3
Dipijat
2,8
Tidak dipijat
7
3,7
Dipijat
3,1
Tidak dipijat
8
3,5
Dipijat
3,2
Tidak dipijat
9
3,6
Dipijat
2,9
Tidak dipijat
10
11
Berat badan perlakuan
3,2
Dipijat
3,3
Tidak dipijat
Design by ; Radi saputra

12. UJI PARAMETRIK – INDEPENDEN
 LANGKAH PENYELESAIAN
1. Penuhi syarat “data harus berdistribusi normal”. Test data dengan
Maka:
langkah berikut:
Berdistribusi Normal bila sig. > 0,05
1. Klik analyze  Descriptive statistics  Expoler
Tidak berdistribusi normal bila sig <0,05
2. Berat badan dipindah ke Depedent list.
3. Perlakuan dipindah ke Factor list.
4. Klik0,05
0,67 > Plots
5. Hilangkan centang Steam-and-leaf, dan centang Histogram.
0,23 > 0,05
6. Centang Normality plots with test. Klik Continue  OK
Kedua data berdistribusi normal, maka T-test Independen dapat
Kemudian analisis pada table “Test of Normality”.
dilanjutkan.
Catatan:
Gunakan Kolmogorov apabila sampel >50
Gunakan Shapiro Wilk apabila sampel <50
Maka yang kita gunakan sekarang adalah nilai signisifikansi Shapiro
Wilk.
12
Design by ; Radi saputra

13. UJI PARAMETRIK – INDEPENDEN
 LANGKAH PENYELESAIAN
2. T-test Jadi nilai variansinya adalah sama, maka digunakan nilai sig. yang
Independent
1. Klik Analyze  Compare means  Independent-Samples T Test
pada baris pertama pada kolom sig (2-tailed)
2. Masukkan berat badan ke Test Variable, dan perlakuan ke Grouping
Variable
H0 diterima : bila sig. > 0,05
3. Kemudian :isikansig. < 0,05 maka H1 diterima. klik Define Group.
H0 ditolak bila group variable dengan cara
Group 1 isi angka 1 (Dipijat), group 2 di isi angka 2 (Tidak dipijat) 
Continue.
Maka
4. Klik Options isi taraf kepercayaan 95% (didapat dari 100% dikurang
0,04 < 0,05
nilaidi terima “berat badan bayi yang dipijat ≠ berat badan bayi
H1 signifikansi(5%))
5. Klik Continue  OK.
yang tidak dipijat.”
Kemudian analisislah pada table output apakan kedua data memiliki
nilai variansi yang sama atau tidak.
Apabila sig. >0,05 variansi sama
Apabila sig <0,05 variansi tidak sama
13
Design by ; Radi saputra

14. UJI PARAMETRIK – DEPENDEN
 Kapan menggunakan uji parametrik DEPENDEN????
digunakan ketika menguji dua sampel berpasangan atau
DEPENDEN. Dalam artian kedua sampel berasal dari sampel atau sub yang
sama namun diukur sebanyak dua kali pengukuran. Yaitu diukur sebelum
dan sesuadah sebuah perlakuan.
 Syarat penggunaan INDEPENDEN
1. Data harus berdistribusi normal
2. Kedua sampelnya DEPENDEN (Berpasangan)
 Contoh :
1. Seorang peneliti ingin mengetahui seberapa signifikan pengaruh
pelatihan marketing yang diikuti oleh sales dalam meningkatkan
prestasi penjualannya. Untuk itu dilakukan pengambilan data 10
orang sampel sales sebelum dan sesudah mengikuti pelatihan.
Dengan signisifikansi 5%.
14
Design by ; Radi saputra

15. UJI PARAMETRIK – DEPENDEN
Berikut data sebelum dan sesuah mengikuti pelatihan :
Nama
Sebelum (unit/hari)
HIPOTESIS :
Sesudah (unit/hari) H0: Rata-rata penjualan sebelum
mengikuti pelatihan = Rata-rata
penjualan
sesudah
mengikuti
14
pelatihan
14
rudi
11
mira
13
angga
13
14
siska
12
13
gotik
12
14
yudi
13
15
jojo
14
16
anto
12
13
stria
13
15
yuyun
14
16
15
H1: Rata-rata penjualan sebelum
mengikuti pelatihan ≠ Rata-rata
penjualan
sesudah
mengikuti
pelatihan
Design by ; Radi saputra

16. UJI PARAMETRIK – DEPENDEN
 LANGKAH PENYELESAIAN
1. Penuhi syarat “data harus berdistribusi normal”. Test data dengan
langkah berikut:
Maka:
1. Klik analyze  Descriptive statistics  Expoler
Berdistribusi Normal bila sig. > 0,05
2. Pindahkan Sebelum_pelatihan sig <0,05
ke
Tidak berdistribusi normal bila dan Sesudah_pelatihan
Depedent list.
3. Klik Satistic, masukkan taraf kepercayaan 95%. Kemudian
Continue. 0,05
0,287 >
4. Klik Plots 0,05
0,177 >
5. Hilangkan centang Steam-and-leaf, dan centang Histogram.
6. Centang data berdistribusi normal, Klik Continue  OK
Kedua Normality plots with test. maka T-test Dependen dapat
Kemudian analisis pada table “Test of Normality”.
dilanjutkan.
Catatan:
Gunakan Kolmogorov apabila sampel >50
Gunakan Shapiro Wilk apabila sampel <50
Maka yang kita gunakan sekarang adalah nilai signisifikansi Shapiro
Wilk.
16
Design by ; Radi saputra

17. UJI PARAMETRIK – DEPENDEN
 LANGKAH PENYELESAIAN
Hipotesis:
2. T-test Dependent
1. H0 diterima : Compare means  Paired-Samples T Test
Klik Analyze bila sig. > 0,05
2. H0 ditolak : bilaSebelum_pelatihan diterima. Variable
Masukkan
1,
dan
sig. < 0,05 maka H1 ke
Sesudah_pelatihan ke Variable 2.
3. Maka
Klik Options isi taraf kepercayaan 95% (didapat dari 100% dikurang
nilai < 0,05
0,000signifikansi(5%))
4. Klik Continue  OK.
H1: Rata-rata penjualan sebelum mengikuti pelatihan ≠ Rata-rata
Kemudian analisislah pada table output.
penjualan sesudah mengikuti pelatihan
17
Design by ; Radi saputra

18. 18
Design by ; Radi saputra