More Related Content
PDF
PDF
SQLアンチパターン 幻の第26章「とりあえず削除フラグ」 PDF
PDF
暗号化したまま計算できる暗号技術とOSS開発による広がり PDF
RSA暗号運用でやってはいけない n のこと #ssmjp PPTX
PPTX
PDF
What's hot
PDF
PDF
PDF
PDF
ヤフー社内でやってるMySQLチューニングセミナー大公開 PDF
PDF
Intro to SVE 富岳のA64FXを触ってみた PDF
PDF
PPTX
katagaitai CTF勉強会 #3 crypto PPTX
PDF
PDF
PPTX
【DL輪読会】Llama 2: Open Foundation and Fine-Tuned Chat Models PDF
PPTX
PDF
Pythonの理解を試みる 〜バイトコードインタプリタを作成する〜 PDF
PDF
コンテナの作り方「Dockerは裏方で何をしているのか?」 PDF
PDF
Similar to 暗号技術入門
PDF
CRYPT+YOU, UNDERSTAND TODAY! PDF
PPT
PDF
PDF
Hacking demonstration 2018 PDF
PDF
PDF
Webアプリでパスワード保護はどこまでやればいいか PDF
Secure scheme script suite PDF
Secure Scheme Script Suite PDF
PDF
PDF
#mailerstudy 02 暗号入門 (2012-02-22更新) PDF
ElGamal型暗号文に対する任意関数演算・再暗号化の二者間秘密計算プロトコルとその応用 PDF
PPT
ODP
Postgre SQL security_20170412 KEY
PPTX
PDF
More from MITSUNARI Shigeo
PDF
PDF
PDF
PDF
PDF
PDF
Intel AVX-512/富岳SVE用SIMDコード生成ライブラリsimdgen PDF
PDF
PDF
深層学習フレームワークにおけるIntel CPU/富岳向け最適化法 PDF
PDF
PDF
Lifted-ElGamal暗号を用いた任意関数演算の二者間秘密計算プロトコルのmaliciousモデルにおける効率化 PDF
PDF
PDF
PDF
PDF
PDF
PDF
A compact zero knowledge proof to restrict message space in homomorphic encry... PDF
暗号技術入門
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
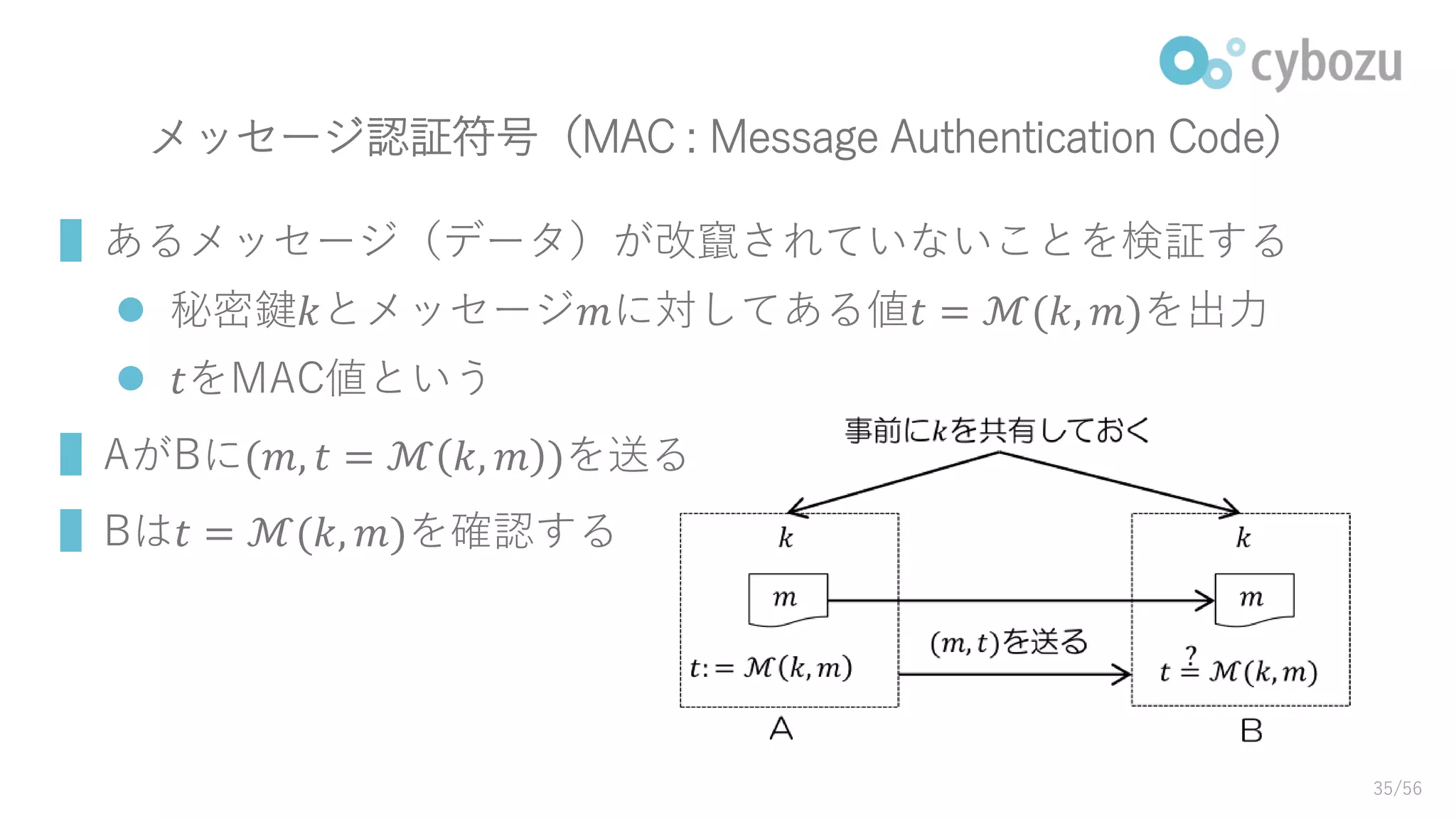
メッセージ認証符号(MAC : MessageAuthentication Code)
▌あるメッセージ(データ)が改竄されていないことを検証する
秘密鍵𝑘とメッセージ𝑚に対してある値𝑡 = ℳ(𝑘, 𝑚)を出力
𝑡をMAC値という
▌AがBに(𝑚, 𝑡 = ℳ 𝑘, 𝑚 )を送る
▌Bは𝑡 = ℳ(𝑘, 𝑚)を確認する
35/56
- 36.
ハッシュ関数で作るMAC : HMAC
▌ℋ𝑘, 𝑚 = 𝐻((𝑘 ⊕ 𝑜𝑝𝑎𝑑)||𝐻((𝑘 ⊕ 𝑖𝑝𝑎𝑑)| 𝑚 )
𝑜𝑝𝑎𝑑, 𝑖𝑝𝑎𝑑はある定数
𝐻を2回使うのがポイント
𝐻(𝑘||𝑚)としてはいけない
▌MACを使うには秘密鍵を相手に送る必要がある
36/56
- 37.
- 38.
- 39.
- 40.
- 41.
公開鍵基盤(PKI : PublicKey Infrastructure)
▌ループを断ち切るための信頼の枠組み
公開鍵証明書
Aの公開鍵が本当にAのものであると証明するもの
認証局
公開鍵証明書の発行や失効手続きを担う機関
認証局も公開鍵証明書を持つ
証明書を検証するときには有効期間や失効していないかも確認する
41/56
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
前方秘匿性(FS : ForwardScrecy)
▌公開鍵暗号の秘密鍵が漏洩(ろうえい)しても
それまでの通信の安全性が保証される仕組み
公開鍵暗号の秘密鍵は長期間使う
▌2013年アメリカ国家安全保障局(NSA)の盗聴・監視が暴露される
Snowdenが利用していたサーバの秘密鍵を裁判所が要求
FS非対応だったため過去のメールの内容が分かってしまう
FSの重要性が強く意識される
50/56
- 51.
- 52.
- 53.
- 54.
- 55.
- 56.
参考文献
▌SSL/TLS 20年の歩みと動向(JPNIC 2015年3月発行)
https://www.nic.ad.jp/ja/newsletter/No59/0800.html
▌TLSの動向(IIR Vol. 31 Jun.2016)
http://www.iij.ad.jp/company/development/report/iir/pdf/iir_v
ol31_trend.pdf
▌いくつかの画像は『クラウドを支える暗号技術』と「いらすとや」
http://herumi.github.io/ango/
http://www.irasutoya.com/
56/56