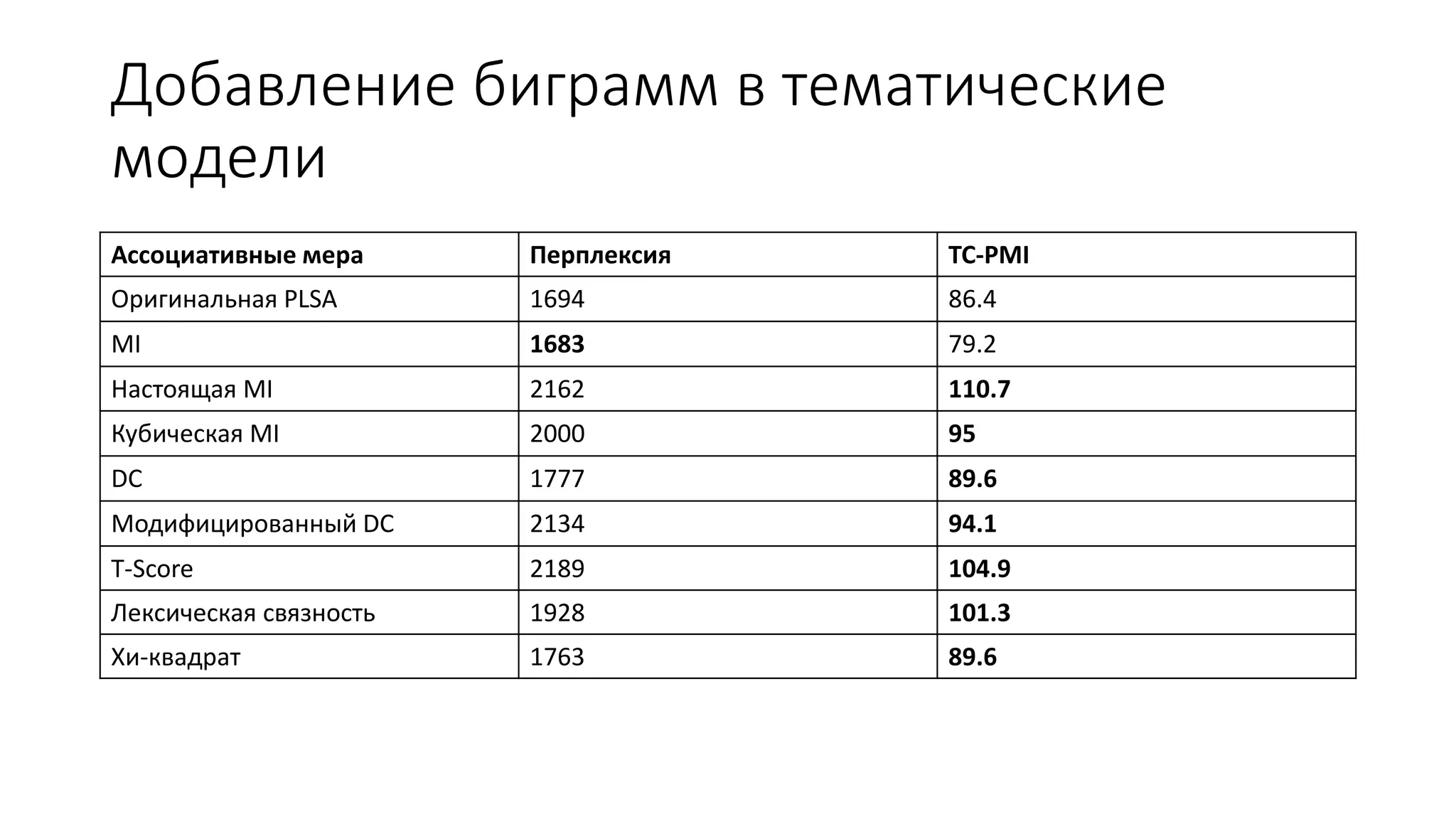
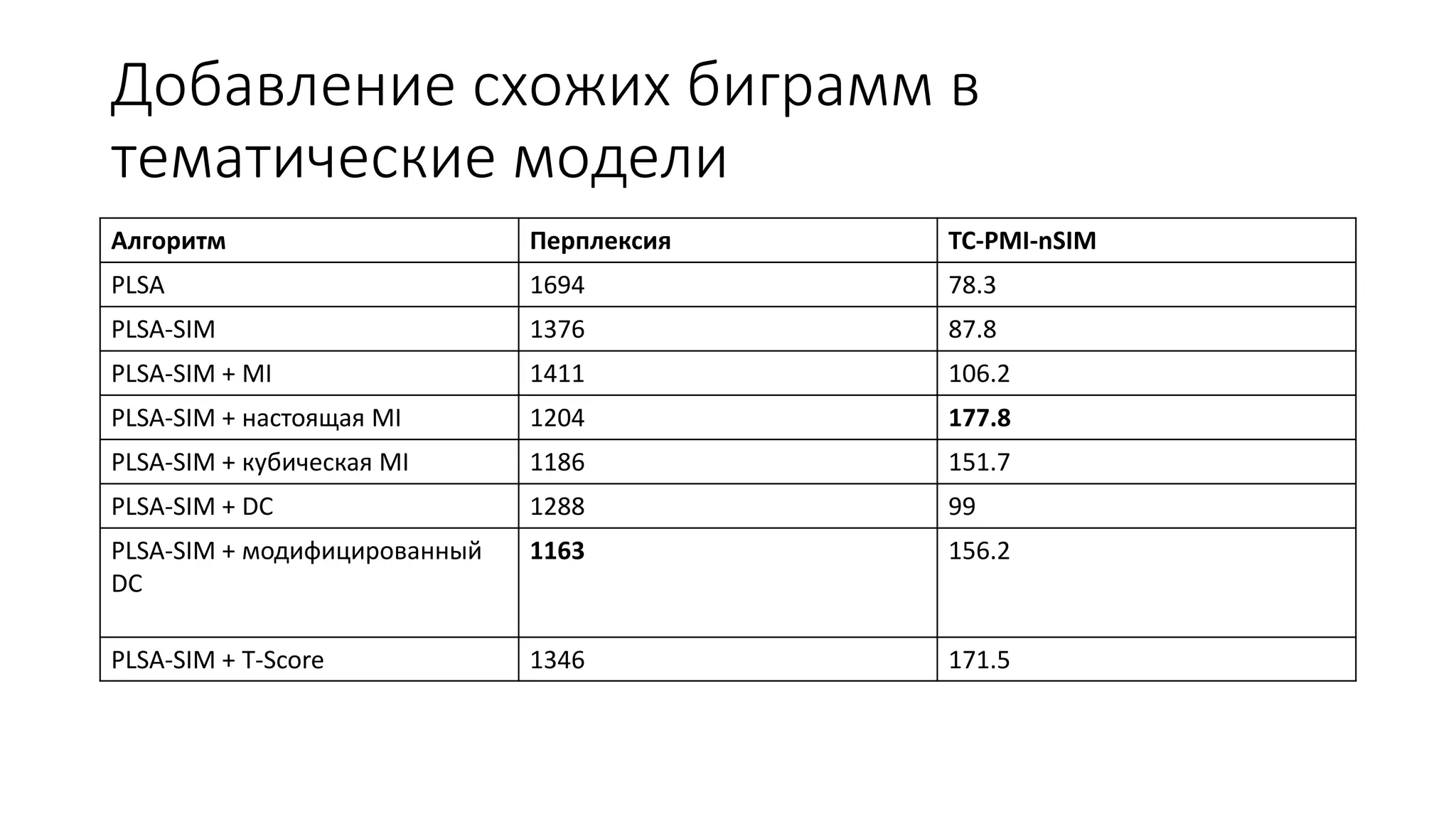
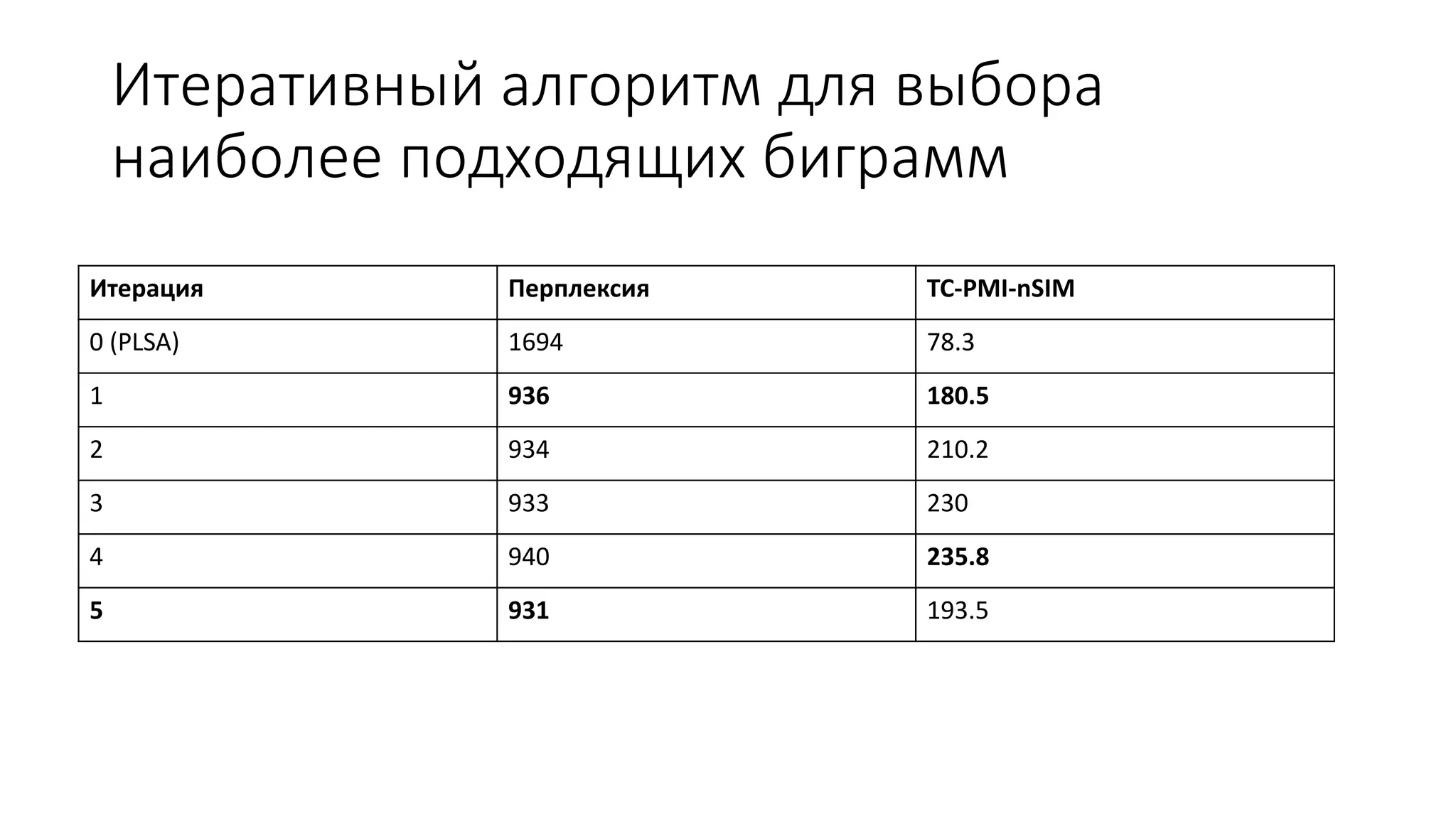
Документ обсуждает тематические модели в контексте информационного поиска и обработки документов, включая вероятностные подходы к моделям 'мешок слов' и их модификации с учетом биграммов и связанных unigram. Он также предлагает новые алгоритмы для добавления словосочетаний в тематические модели, оценивая их качество с помощью различных метрик, таких как perplexity и tc-pmi. Вместе с примерами применения моделей на большом наборе русскоязычных статей, документ подчеркивает важность улучшения алгоритмов для повышения точности тематического анализа.