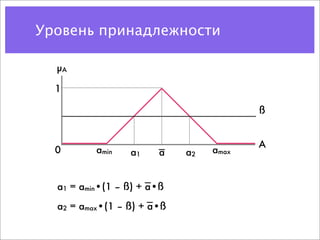
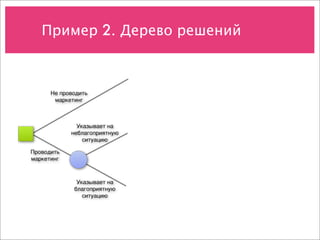
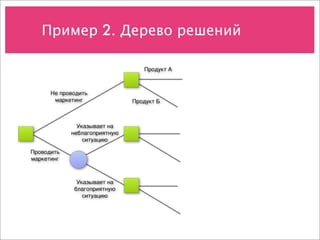
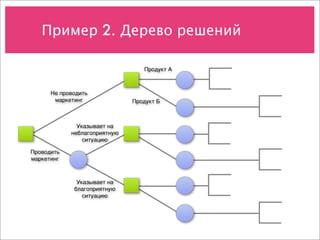
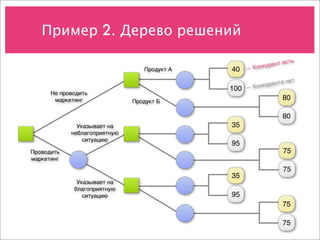
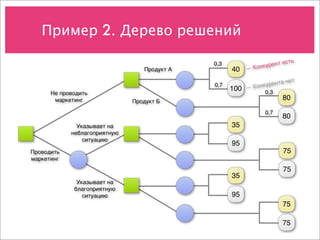
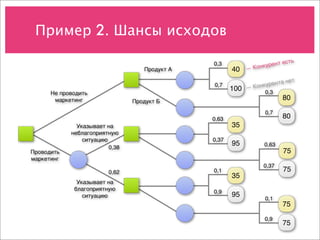
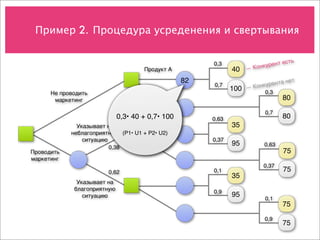
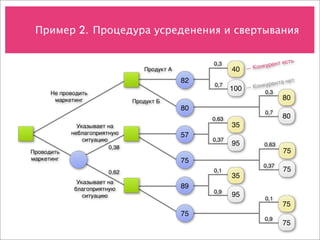
Документ охватывает учет рисков и различные модели принятия решений в условиях неопределенности, включая анализ дисконтирования, деревья решений и модели оценки опционов. Примеры направлены на демонстрацию применения этих концепций для оценки стоимости проектов и потоков денежных средств. Также рассматриваются методы прогнозирования, биноминальные модели и возможности менеджмента при инвестировании в новые продукты.


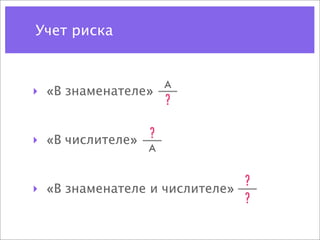
















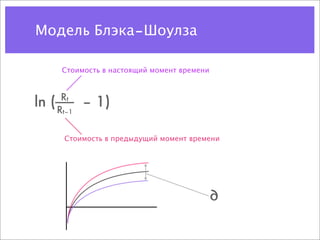









![Цена опциона на покупку
Никто не станет платить за опцион на покупку
актива больше, чем разница между тем, что нужно
заплатить для покупки актива на рынке, и тем, что
нужно запатить по опциону, т.е. ценой
исполнения.
Цена актива на рынке
С = max[0, S – K]
Стоимость колл-опциона Цена исполнения опциона](https://image.slidesharecdn.com/4-091119125957-phpapp01/85/slide-51-320.jpg)
![Цена опциона на продажу
В случае опциона на продажу актива никто не
будет платить за этот опцион больше, чем разница
между ценой, по которой актив может быть продан
на открытом рынке, и ценой, по которой этот
актив будет продан по опциону.
Цена актива на рынке
P = max[0, K – S]
Стоимость пут-опциона Цена исполнения опциона](https://image.slidesharecdn.com/4-091119125957-phpapp01/85/slide-52-320.jpg)


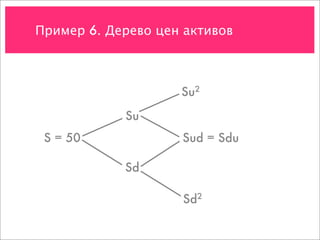
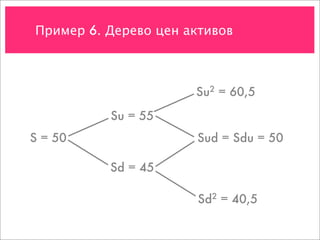
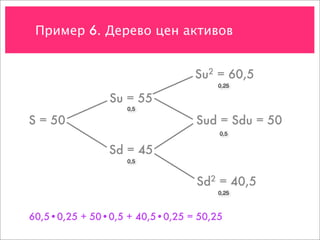
![Пример 7. Создание портфеля-имитатора
Стоимость актива Su = 43,75
S = 35
Sd = 26,25
Стоимость опциона Cu = max[0, 43,75 – 35] = 8,75
C
Cd = max[0, 26,25 – 35] = 0](https://image.slidesharecdn.com/4-091119125957-phpapp01/85/slide-55-320.jpg)




![Пример 7. Создание портфеля-имитатора
Если R = (1 + r), где r — безрисковая процентная ставка,
тогда:
R•(S – H•C) = Su – H•Cu
C=
[ Cu•
R–d
u–d
+ Cd•
u–R
u–d ] /R](https://image.slidesharecdn.com/4-091119125957-phpapp01/85/slide-60-320.jpg)
![Пример 7. Создание портфеля-имитатора
C=
[
8,75•
1,1– 0,75
1,25 – 0,75
+ 0•
1,25 – 1,1
1,25 – 0,75 ] / 1,1 = 5,57](https://image.slidesharecdn.com/4-091119125957-phpapp01/85/slide-61-320.jpg)



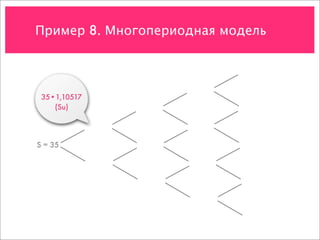
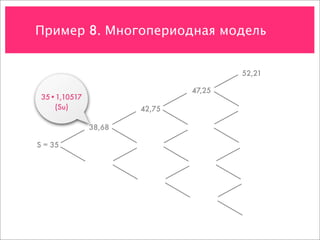
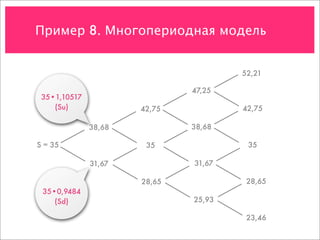
![Пример 8. Многопериодная модель
C = max[0, S – K]
52,21
47,25
42,75
…
38,68
35
…
31,67
28,65
…
25,93
23,46](https://image.slidesharecdn.com/4-091119125957-phpapp01/85/slide-68-320.jpg)
![Пример 8. Многопериодная модель
C = max[0, S – K]
52,21
17,21 C = max[0, 52,21 – 35] = 17,21
47,25
42,75
…
38,68
35
…
31,67
28,65
…
25,93
23,46](https://image.slidesharecdn.com/4-091119125957-phpapp01/85/slide-69-320.jpg)
![Пример 8. Многопериодная модель
C = max[0, S – K]
52,21
17,21 C = max[0, 52,21 – 35] = 17,21
47,25
42,75
…
7,75 C = max[0, 42,75 – 35] = 7,75
38,68
35
…
0 C = max[0, 35 – 35] = 0
31,67
28,65
…
0 C = max[0, 28,65 – 35] = 0
25,93
23,46
0 C = max[0, 23,46 – 35] = 0](https://image.slidesharecdn.com/4-091119125957-phpapp01/85/slide-70-320.jpg)
![[
C= Cu•
R–d
u–d]/R
+ Cd•
u–R
Пример 8. Многопериодная модель
u–d
C= [ Cu• 0,5948 + Cd• 0,4052 ] / 1,024
52,21
17,21
47,25
13,07
42,75 42,75
7,75
38,68 38,68
35 35
S = 35
0
31,67 31,67
28,65 28,65
0
25,93
23,46
0](https://image.slidesharecdn.com/4-091119125957-phpapp01/85/slide-71-320.jpg)
![[
C= Cu•
R–d
u–d]/R
+ Cd•
u–R
Пример 8. Многопериодная модель
u–d
C= [ Cu• 0,5948 + Cd• 0,4052 ] / 1,024
52,21
17,21
47,25
13,07
42,75 42,75
9,38 7,75
38,68 38,68
6,48 4,51
S = 35 35 35
C = 4,37 2,62 0
31,67 31,67
1,52 0
28,65 28,65
0 0
25,93
0
23,46
0](https://image.slidesharecdn.com/4-091119125957-phpapp01/85/slide-72-320.jpg)









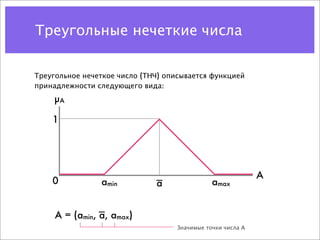
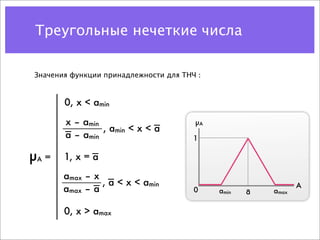
![Треугольные нечеткие числа
Допустим есть два нечетких числа A и B их интервалы
принадлежности [amin, amax] и [bmin, bmax] соответственно, тогда
операции с этими интервалами выражаются через операции с
действительными числами по следующим правилам:
[amin, amax] + [bmin, bmax] = [amin + bmin, amax + bmax]
[amin, amax] – [bmin, bmax] = [amin – bmax, amax – bmin]
[amin, amax] • [bmin, bmax] = [amin•bmin, amax•bmax]
[amin, amax] / [bmin, bmax] = [amin / bmax, amax / bmin]
[amin, amax]n = [aminn, amaxn]](https://image.slidesharecdn.com/4-091119125957-phpapp01/85/slide-84-320.jpg)
![Вычисления с нечеткими числами
В результате расчетов с ТНЧ также
получаются нечеткие числа:
T
CF
NPV = ∑ (1 + i)n
n=1
[NPVmin, NPV, NPVmax]](https://image.slidesharecdn.com/4-091119125957-phpapp01/85/slide-85-320.jpg)
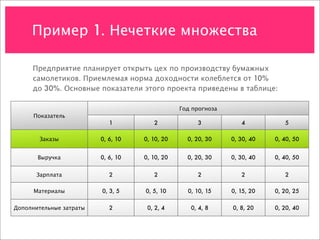
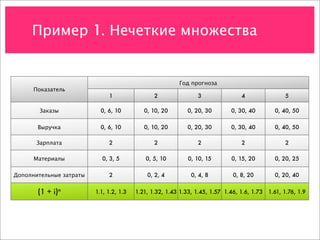
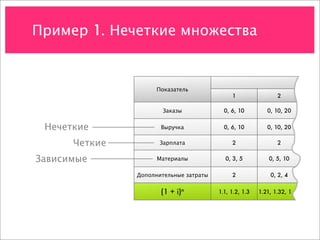

![Пример 1. Нечеткие множества
Год прогноза
Показатель
1 2 3 4 5
Заказы 0, 6, 10 0, 10, 20 0, 20, 30 0, 30, 40 0, 40, 50
Выручка 0, 6, 10 0, 10, 20 0, 20, 30 0, 30, 40 0, 40, 50
Зарплата 2 2 2 2 2
Материалы 0, 3, 5 0, 5, 10 0, 10, 15 0, 15, 20 0, 20, 25
Доп. затраты 2 0, 2, 4 0, 4, 8 0, 8, 20 0, 20, 40
(1 + i)n 1.1, 1.2, 1.3 1.21, 1.32, 1.43 1.33, 1.45, 1.57 1.46, 1.6, 1.73 1.61, 1.76, 1.9
1) Выручка –
–2, 1, 3 –2, 3, 8 … … …
– Зарплата – Материалы
2) [1] – Доп. затраты –4, –1, 1 –6, 1, 8 … … …
DCF –4/1.3, … … … … …](https://image.slidesharecdn.com/4-091119125957-phpapp01/85/slide-90-320.jpg)