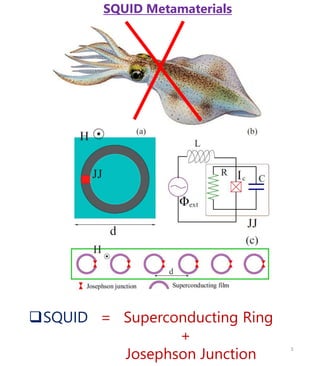
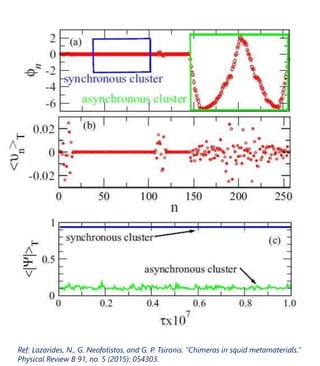
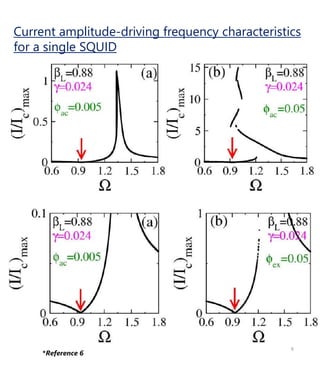
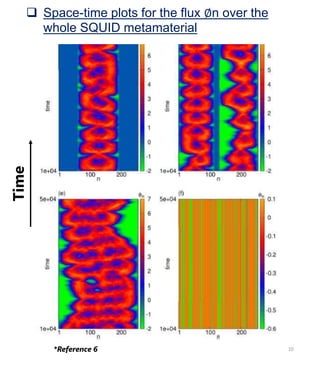
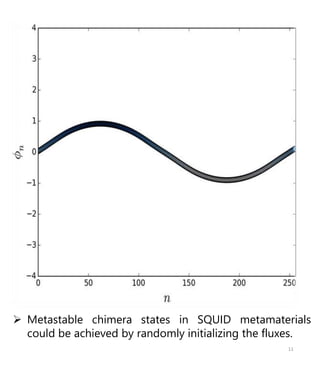
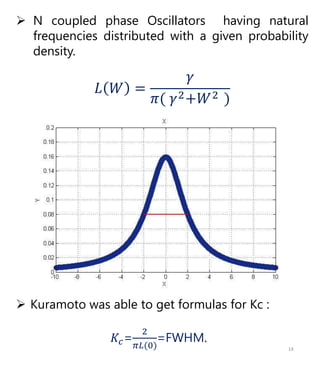
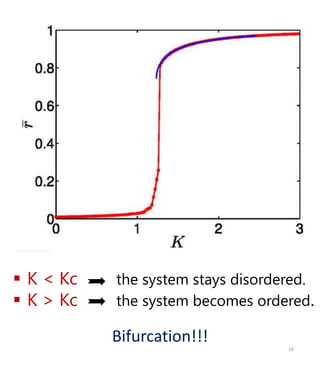
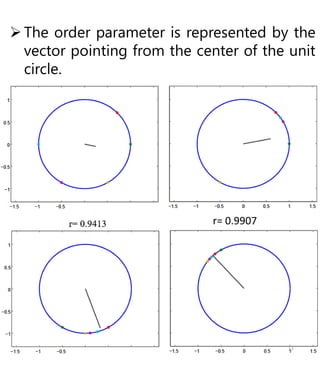
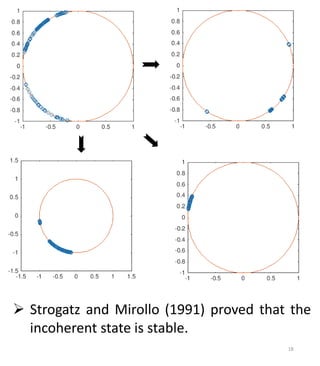
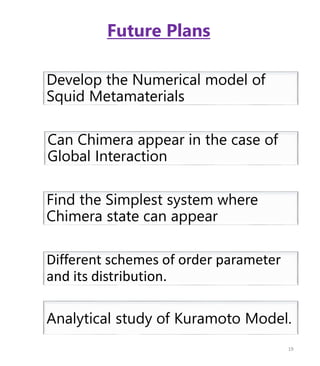
The document discusses squid metamaterials and their characteristics, particularly the concept of chimera states within these materials based on the Kuramoto model of synchronized oscillators. It highlights the unique properties of squid metamaterials, such as low loss and nonlinearity, while also outlining future research directions. The goal includes exploring the conditions under which chimera states can emerge from global interactions within these quantum systems.

1. CHIMEARS IN SQUID
METAMATERIALS
WITH GLOBAL INTERACTION
Premashis Kumar
2016msph005
Project Advisor: Prof. Manish Dev Shrimali
1

2. CONTENTS
• Introduction
• SQUID Metamaterials
• Chimeras in SQUID
Metamaterials
• Kuramoto Model
• Future Planning
2

3.  First described theoretically by Victor
Veselago in 1967.
 John Pendry identified a practical way to
make a left-handed metamaterial in 1999.
 A material engineered to have properties,
not found in nature.
3
Introduction

4. o Ref: Zheludev, Nikolay I. "The road ahead for metamaterials." Science 328, no. 5978 (2010):
582-583.
4

5. SQUID = Superconducting Ring
+
Josephson Junction
5
SQUID Metamaterials

6. Advantages
(A) Low loss.
(B) Compact dimensions.
(C) Nonlinearity, tuning & switching.
Limiting Factors
 Critical temperature Tc
 Gap frequency ∼2Δ(T)/h
Key Factors
1) Geometry
2) Superconductivity and Josephson
effect.
6

7. 7

8. Ref: Lazarides, N., G. Neofotistos, and G. P. Tsironis. "Chimeras in squid metamaterials."
Physical Review B 91, no. 5 (2015): 054303.
8

9. Current amplitude-driving frequency characteristics
for a single SQUID
9
*Reference 6

10.  Space-time plots for the flux ∅n over the
whole SQUID metamaterial
10*Reference 6
Time

11.  Metastable chimera states in SQUID metamaterials
could be achieved by randomly initializing the fluxes.
11

12. Kuramoto Model
12

13.  The Kuramoto model is a mean field
model.
 Assumptions:
I. Identical Oscillators.
II. Weak coupling.
 General system of coupled oscillators
𝜃𝑖=𝑤𝑖 + 𝑗=1
𝑁
Γ𝑖𝑗
 In Kuramoto Model, Interaction function
Γ𝑖𝑗=
𝐾
𝑁
sin(𝜃𝑗−𝜃𝑖)
 Each oscillator takes part in affecting
others “Global Interaction”.
13

14.  N coupled phase Oscillators having natural
frequencies distributed with a given probability
density.
𝐿 𝑊 =
𝛾
𝜋( 𝛾2+𝑊2 )
 Kuramoto was able to get formulas for Kc :
𝐾𝑐=
2
𝜋𝐿(0)
=FWHM.
14

15.  Complex Order parameter:
R=
1
𝑁 𝑗=1
𝑁
𝑒 𝑖𝜃 𝑗(𝜏)
The Order Parameter
 Phases of the oscillators represented as points on
the unit circle: 𝑒 𝑖𝜃.
 We can also represent R as 𝑟𝑒 𝑖𝜙
.
r Measure of the phase coherence.
𝜙 Average phase.
 𝑟 = 1 −
𝐾 𝑐
𝐾
 Describes strength of synchrony of those
identical oscillators.
 Simplify the governing equation of Kuramoto
model : 𝜃𝑖= 𝑤𝑖 +Krsin(ψ−𝜃𝑖) 15

16.  K < Kc the system stays disordered.
 K > Kc the system becomes ordered.
Bifurcation!!!
16

17. The order parameter is represented by the
vector pointing from the center of the unit
circle.
17
r= 0.9907

18.  Strogatz and Mirollo (1991) proved that the
incoherent state is stable.
18

19. 19
Future Plans
Different schemes of order parameter
and its distribution.
Can Chimera appear in the case of
Global Interaction
Find the Simplest system where
Chimera state can appear
Develop the Numerical model of
Squid Metamaterials
Analytical study of Kuramoto Model.

20. References
1. Lazarides, N., G. Neofotistos, and G. P. Tsironis. "Chimeras in
squid metamaterials." Physical Review B 91, no. 5 (2015):
054303.
2. Acebrón, Juan A., Luis L. Bonilla, Conrad J. Pérez Vicente, Félix
Ritort, and Renato Spigler. "The Kuramoto model: A simple
paradigm for synchronization phenomena." Reviews of modern
physics 77, no. 1 (2005): 137.
3. Jung, Philipp, Alexey V. Ustinov, and Steven M. Anlage.
"Progress in superconducting metamaterials." Superconductor
Science and Technology 27, no. 7 (2014): 073001.
4. Zheludev, Nikolay I. "The road ahead for metamaterials."
Science 328, no. 5978 (2010): 582-583.
5. N. Yao, Z.-G. Huang, Y.-C. Lai, and Z.-G. Zheng, Sci. Rep. 3, 3522
(2013)
6. Hizanidis, J., Lazarides, N., Neofotistos, G., & Tsironis, G. P.
(2016). Chimera states and synchronization in magnetically
driven SQUID metamaterials. The European Physical Journal
Special Topics, 225(6-7), 1231-1243.
7. Wu, H., & Kim, D. (2015). Distribution of Order Parameter for
Kuramoto Model. International Journal for Innovation Education
and Research, 3(9).
8. Gottwald, G. A. (2015). Model reduction for networks of coupled
oscillators. Chaos: An Interdisciplinary Journal of Nonlinear Science,
25(5), 053111.
20

21. 21