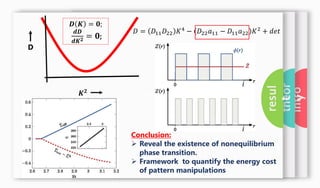
This document summarizes a research paper on the thermodynamics of Turing patterns. The paper presents a theoretical framework for analyzing Turing patterns as nonequilibrium phase transitions. Key results include: 1) Deriving reaction-diffusion equations to model Turing pattern formation driven by nonlinear feedback and diffusion. 2) Developing expressions for the Gibbs free energy and entropy production of the system based on these equations. 3) Revealing that Turing patterns represent nonequilibrium phase transitions through analyzing the Jacobian and showing the system can extremize energy.

1. intro
theory
result
Information Thermodynamics of Turing Patterns
~Gianmaria Falasco, Riccardo Rao, and Massimiliano Esposito
(Complex Systems and Statistical Mechanics, University of Luxembourg)
DOI: 10.1103/PhysRevLett.121.108301
I. INTRODUCTION
II. MOTIVATION
III. THEORY
IV. TURING
PATTERN
V. CONCLUSIONS
CONTENTS
 Nonlinear feedback effects destabilized by
diffusion Reaction-diffusion systems
searching for general
extremum principles
Research focus :
 Continual influx of chemicals and energy
for dissipative structures
 complete framework is still lacking-
necessary for technological applications
Work
needed to
manipulate
a Turing
pattern
Efficiency of
exchanging
information
through
traveling
waves
Turing patterns
as
thermodynamic
nonequilibrium
phase
transitionsBy PREMASHIS KUMAR

2. intro
𝒖
𝒗
=
𝒂 𝟏𝟏 𝒂 𝟏𝟐
𝒂 𝟐𝟏 𝒂 𝟐𝟐
𝒖
𝒗
𝝀 𝟐
− 𝐓𝐫 𝛌 + 𝒅𝒆𝒕 = 𝟎
Tr=𝝀 𝟏 + 𝝀 𝟐 < 𝟎
𝒅𝒆𝒕 = 𝝀 𝟏 𝝀 𝟐>0
theor
y
resul
t
𝜕𝑍 𝜎
𝜕t
=-⩢.𝐽 𝜎 + ρ 𝑆𝜌
𝜎
jρ + 𝐼 𝜎
Reaction-Diffusion equation:
−𝑫 𝝈 ⩢ 𝒁 𝝈
Fick’s diffusion
current :
Stoichiometry
Matrix
'Canonical'Gibbs free energy
𝑮 = 𝑽
𝒅𝒓 𝝈(𝝁 𝝈 𝒁 𝝈 − 𝒁 𝝈)
𝑮 = 𝑮 𝒆𝒒 + ℒ(𝒁 𝝈||𝒁 𝝈
𝒆𝒒
)
ℒ(𝒁 𝝈||𝒁 𝝈
𝒆𝒒
)= 𝑽
𝒅𝒓 𝝈(𝒁 𝝈 𝒍𝒏
𝒁 𝝈
𝒁 𝝈
𝒆𝒒 − (𝒁 𝝈 − 𝒁 𝝈
𝒆𝒒
)
Conservative laws : 𝒙 𝒍 𝒙
𝝀 𝑺 𝝆
𝒙 = 𝟎
𝒙 𝒍 𝒙
𝝀 𝒖
𝑺 𝝆
𝒙 = 𝟎, 𝒙 𝒍 𝒙
𝝀 𝒃
𝑺 𝝆
𝒙 ≠ 𝟎 (For open system)
𝓛 = 𝑮= 𝒅 − 𝒓=− ≤ 𝟎
EPR
𝒙 𝒔, 𝒚 𝒔
Jacobian
𝕁 𝑫 =
𝒂 𝟏𝟏− 𝑫 𝟏𝟏 𝑲 𝟐 𝒂 𝟏𝟐
𝒂 𝟐𝟏 𝒂 𝟐𝟐 − 𝑫 𝟐𝟐 𝑲 𝟐

3. intro
theor
y
Det
resul
t
D
𝑲 𝟐
𝑫 𝑲 = 𝟎;
𝒅𝑫
𝒅𝑲 𝟐 = 𝟎;
𝐷 = 𝐷11 𝐷22 𝐾4
− 𝐷22 𝑎11 − 𝐷11 𝑎22 𝐾2
+ 𝑑𝑒𝑡
Conclusion:
 Reveal the existence of nonequilibrium
phase transition.
 Framework to quantify the energy cost
of pattern manipulations