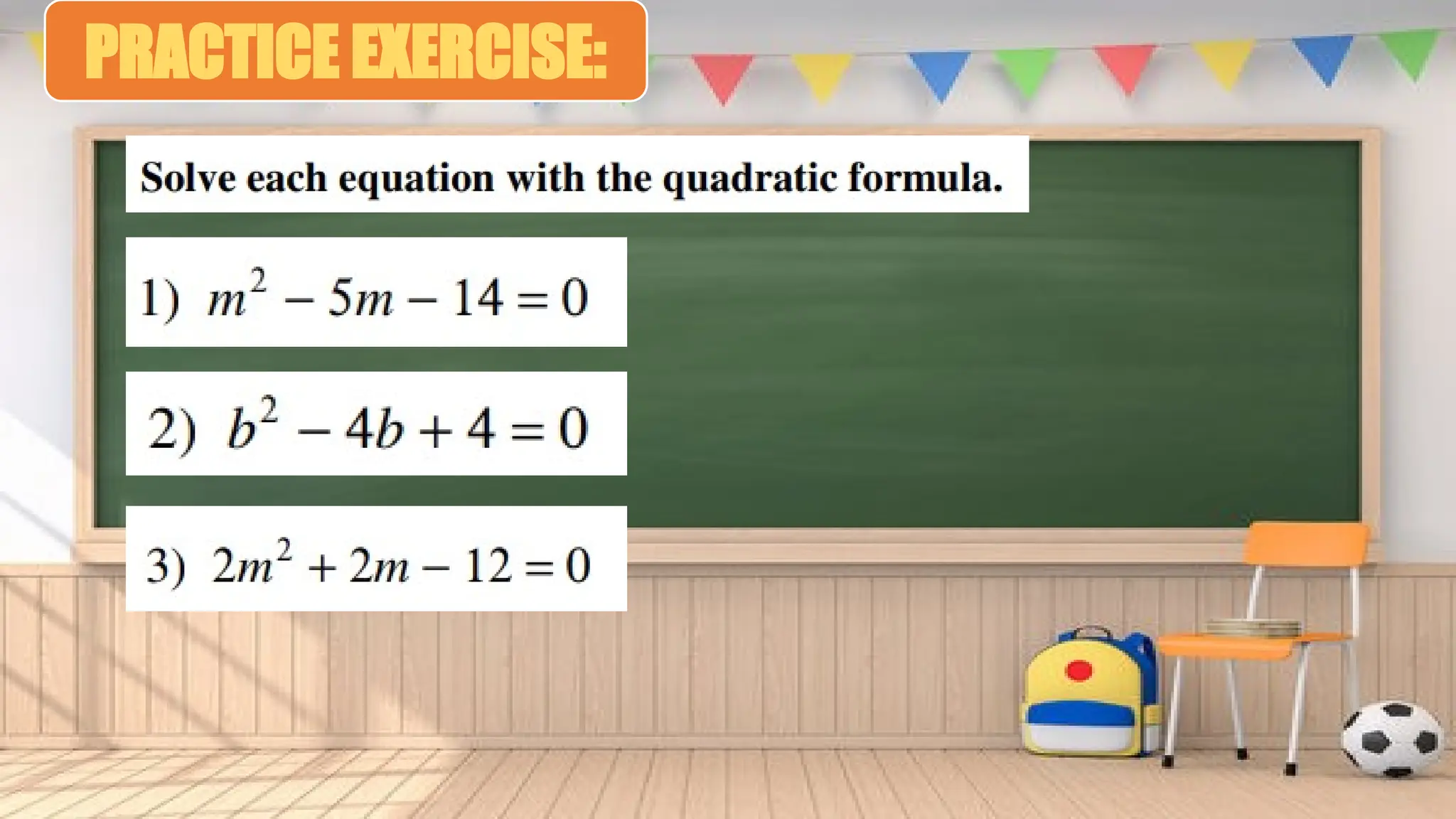The document provides a lesson on solving quadratic equations using the quadratic formula, detailing its definition and significance in finding roots regardless of factorization. It includes step-by-step examples demonstrating the application of the formula to various quadratic equations. Additionally, it concludes with a practice exercise for reinforcement.