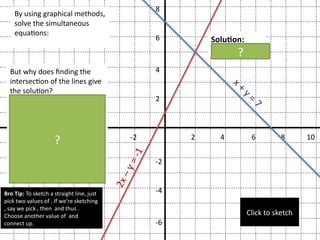
The document provides an educational overview of solving simultaneous equations using graphical methods, elimination, and substitution techniques. It discusses the conditions for having no solutions, infinitely many solutions, and emphasizes the process of finding intersections in graphical solutions. Additionally, it includes exercises and examples to reinforce understanding of the concepts presented.

1. Year 9: Simultaneous Equations
Dr J Frost (jfrost@tiffin.kingston.sch.uk)
www.drfrostmaths.com
Last modified: 13th
September 2015

2. 𝑥 2=4
𝑥=3
𝑥+ 𝑦=9
For For
1 ∞
2 ∞
∞ ∞
1 1
? ?
? ?
? ?
? ?
How many solutions for x and y?
Hint: Think about the line
representing

3. -10 -8 -6 -4 -2 2 4 6 8 10
8
6
4
2
-2
-4
-6
By using graphical methods,
solve the simultaneous
equations:
2
x
–
y
=
-
1
x
+
y
=
7
Click to sketch
But why does finding the
intersection of the lines give
the solution?
1. The line for each
equation represents all
the points (x,y) for which
the equation is satisfied.
2. Therefore, at the
intersection(s), this gives
the points for which both
equations are satisfied.
?
Solution:
Bro Tip: To sketch a straight line, just
pick two values of . If we’re sketching
, say we pick , then and thus .
Choose another value of and
connect up.
?

4. Test Your Understanding
Copy the axis provided, and sketch the given lines on them*.
Hence solve the simultaneous equations.
𝑥
𝑦 𝑦=2 𝑥−2 𝑥+ 𝑦=4
𝑥=2, 𝑦=2
𝑥
𝑦 𝑦 −𝑥=1 𝑦=−3𝑥+5
𝑥=1, 𝑦=2
Q1 Q2
1 2 3 4 5
5
4
3
2
1
5
4
3
2
1
1 2 3 4 5
* Remember that the easiest way is to pick two points and join up, e.g. when and when .

5. www.wolframalpha.com

6. Thinking graphically…
For two simultaneous equations, when would we have…
0 solutions for and ? Lines are parallel but not
the same.
Infinitely many solutions
for and ?
Lines are the same.
e.g.
?
?

7. Exercise 1
For each of the following, sketch axis for from 0
to 6 and from 0 to 6. Sketch the two lines on
your axis and use them to estimate the solution
to the simultaneous equations.
Consider the simultaneous equations:
where and are constants. By thinking about the
lines corresponding to the equations, under
what conditions will we have:
a) Infinitely many solutions for and ?
b) No solutions:
For each of the following, sketch axis for from -
5 to 5 and from -5 to 5. Sketch the two lines on
your axis and use them to estimate the solution
to the simultaneous equations.
Given that:
Sketch suitable lines to estimate the solutions to
these simultaneous equations.
1
2
3
a
b
c
a
b
c
N
?
?
?
?
?
?
?
?
?

8. Three methods of solving simultaneous equations
graphically
by elimination
by substitution

9. By either adding or subtracting the equations, we can ‘eliminate’ one of the variables.
METHOD #2: Solving by Elimination
2𝑥+𝑦=61
2
Bro Tip: I strongly urge you to
number your equations. This
becomes crucial when you have
three equations/three
unknowns, so that you can
indicate which equations you
are combining.
2
1 +
Obtain by substituting
your known into one
of the two equations.
4𝑥+𝑦=61
2
1
2 -
2𝑥=−2
?
?

10. You can solve in 2
different ways:
•Eliminating .
•Eliminating .
𝑥=3, 𝑦=−1
?
Solving by Elimination
1+2
?

11. Test Your Understanding
𝑥=4, 𝑦=2
𝑥=−1, 𝑦=5
𝑥=9, 𝑦=−4
?
?
?
If you finish quickly:
1+2
1+3
2+3
?

12. [Kangaroo Grey 2013 Q6] The positive integers 𝑥,𝑦 and 𝑧
satisfy
What is the value of 𝑥+𝑦+𝑧?
Elimination by other means
Multiplying the equations:
Thus ?

13. Exercise 2
Solve the following by
elimination.
[Cayley 2004 Q2] Mars, his wife Venus and
grandson Pluto have a combined age of 192.
The ages of Mars and Pluto together total 30
years more than Venus’ age. The ages of
Venus and Pluto together total 4 years more
than Mars’s age. Find their three ages.
Hint: You can form 3 equations with 3 unknowns
Mars = 94, Venus = 81, Pluto = 17
[Cayley 2012 Q3] Three loaves of bread, five
cartons of milk and four jars of jam cost
£10.10. Five loaves of bread, nine cartons of
milk and seven jars of jam cost £18.20. How
much does it cost to buy one loaf of bread,
one carton of milk and one jar of jam?
Solution: £2
[Maclaurin 2006 Q2] Find all integer values
that satisfy the following equations:
Adding:
When
When
Thus
Two cats and a dog cost
£91. Three cats and two
dogs cost £159. How much
does a cat cost?
£23
Solve:
Solve
1
a
b
c
d
3 a
b
c
5
N
1
N
2
4
?
?
?
?
?
?
?
?
?
?
?
N
3
[IMC 2004 Q5] The sum of
two numbers is 2. The
difference between them is
4. What is their product? -3
2
?
6
?
?

14. by substitution
Three methods of solving simultaneous equations
graphically
by elimination

15. We currently have two equations both involving two variables.
Perhaps we could put one equation in terms of or , then substitute this expression into
the other.
𝟐 𝒙+ 𝒚=𝟕 𝒚 =𝟕 – 𝟐 𝒙
Then
?
METHOD #3: Solving by Substitution
Why do you think we chose this
equation to rearrange?
?

16. Answer:
x = 2, y = 1
?
Check Your Understanding
Answer:
?
Solve for and , using substitution.

17. Exercise 3
Use substitution only to solve the following simultaneous equations.
[Cayley] James, Alison and Vivek go into a
shop to buy some sweets. James spends
£1 on four Fudge Bars, a Sparkle and a
Chomper. Alison spends 70p on three
Chompers, two Fudge Bars and a Sparkle.
Vivek spends 50p on two Sparkles and a
Fudge Bar. What is the cost of a Sparkle?
Sparkle = 15p
[Maclaurin] Solve the simultaneous
equations:
(You must have proved algebraically, using
substitution, that these are the only solutions)
[Maclaurin] Solve:
(Hint: If after substitution you end up with a cubic
equation, you can sometimes factorise it by
factorising the first two terms and the last two terms
first separately)
𝑥
𝑥
3 𝑦
A
B
C
The angle at is 12° greater than the
angle at . Find and .
Gus wants to buy 80 Ferraris, some
yellow and some red. He must spend
the whole of the £20m of his weekly
pocket money. He buys yellow Ferraris
at £40k and red Ferraris at £320k. How
many Ferraris of each type did he buy?
1 2
3
5
N1
N2
?
?
?
?
?
?
?
?
?
?
£13 £19 £17
4 What is the
cost of a cat?
£1
a
b
c
d
e
?

18. by substitution
Three methods of solving simultaneous equations
graphically
by elimination
SECRET LEVEL
by matrices
(you’ll have to
wait for Further
Maths A Level for
this one)