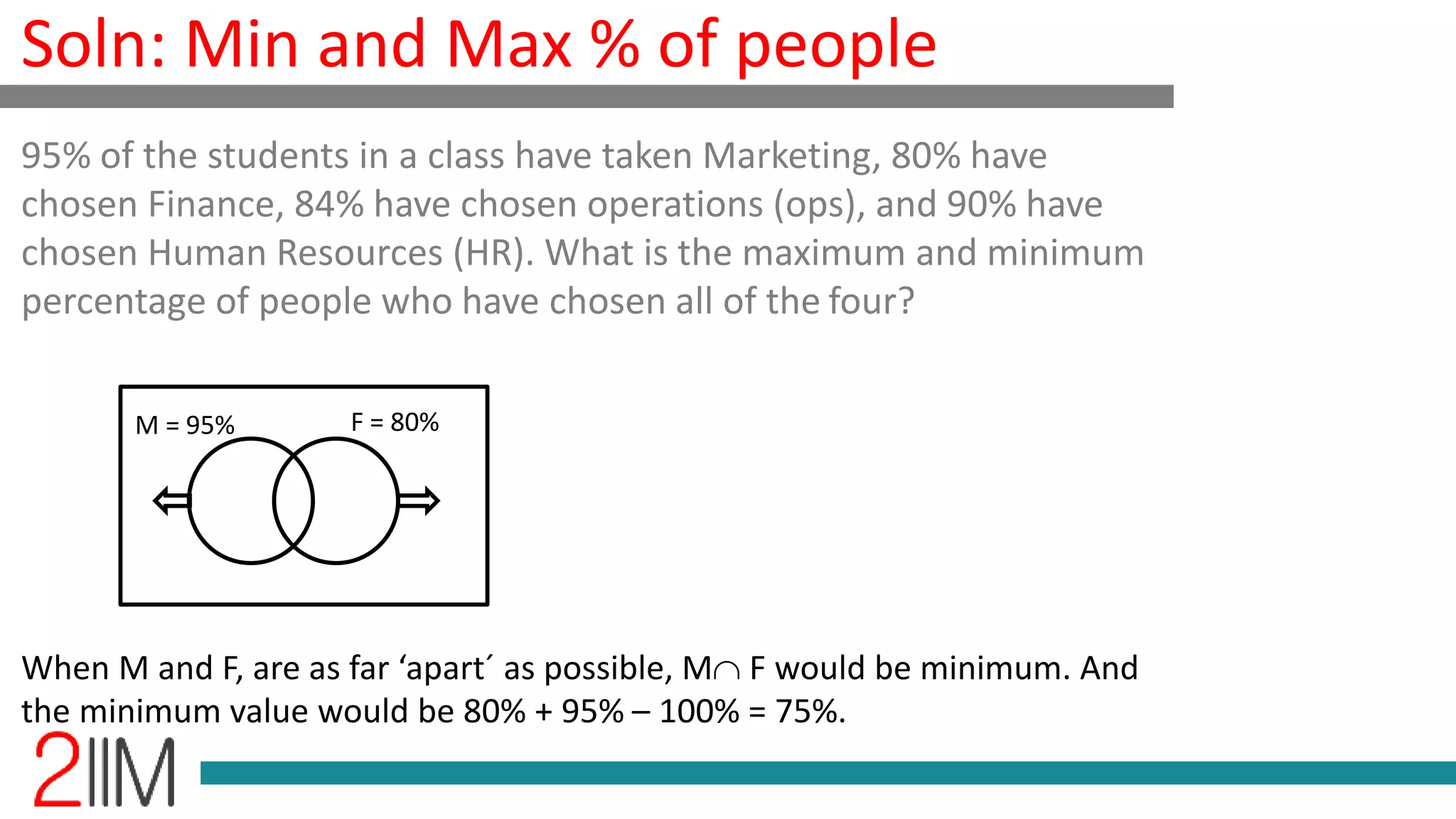
The document discusses the maximum and minimum percentages of students who have taken four subjects: marketing, finance, operations, and human resources. The maximum percentage of students taking all four subjects is 80%, while the minimum is calculated to be 49% through various iterations and formula applications. It emphasizes that understanding through trial and error is beneficial over solely relying on formulas.

1. Set Theory Q7

2. Qn: Min and Max % of people
(a) 80% and 56% (b) 95% and 53%
(c) 80% and 49% (d) 80% and 51%
95% of the students in a class have taken Marketing, 80% have
chosen Finance, 84% have chosen operations (ops), and 90% have
chosen Human Resources (HR). What is the maximum and minimum
percentage of people who have chosen all of the four?

3. Soln: Min and Max % of people
Finding the maximum percentage is easy. If F  O  H  M, then the
percentage of people who have taken all 4 should be 80% and this is the
maximum value it can take.
For the value to be minimum, the numbers should be as far ‘apart´ as
possible. Let us do this iteratively. First, let us take Marketing and Finance,
and see if we can find the minimum percentage of students who should
have taken both.
95% of the students in a class have taken Marketing, 80% have
chosen Finance, 84% have chosen operations (ops), and 90% have
chosen Human Resources (HR). What is the maximum and minimum
percentage of people who have chosen all of the four?

4. Soln: Min and Max % of people
When M and F, are as far ‘apart´ as possible, M F would be minimum. And
the minimum value would be 80% + 95% – 100% = 75%.
95% of the students in a class have taken Marketing, 80% have
chosen Finance, 84% have chosen operations (ops), and 90% have
chosen Human Resources (HR). What is the maximum and minimum
percentage of people who have chosen all of the four?
M = 95% F = 80%

5. Soln: Min and Max % of people
Now, let us start with this M F and add Ops to the mix.
Now, the minimum value of M  F  O would be when these are as far
‘apart’ as possible. And the minimum value would be 75% + 84% – 100% =
59%.
95% of the students in a class have taken Marketing, 80% have
chosen Finance, 84% have chosen operations (ops), and 90% have
chosen Human Resources (HR). What is the maximum and minimum
percentage of people who have chosen all of the four?
MF = 75% O = 84%

6. Soln: Min and Max % of people
Adding HR also to the mix, we get
The minimum possible value of M  F  O  H = 59% + 90% – 100% = 49%.
95% of the students in a class have taken Marketing, 80% have
chosen Finance, 84% have chosen operations (ops), and 90% have
chosen Human Resources (HR). What is the maximum and minimum
percentage of people who have chosen all of the four?
MFO = 59% H = 90%

7. Soln: Min and Max % of people
As a formula, the minimum value is 100% – (100% – 95%) – (100% – 80%) –
(100% – 84%) – (100% – 90%).
= 100% – 5% – 20% – 16% – 10% = 100% – 51% = 49%.
Again, do not go with just the formula. See the trial and error iteration. The
trial and error iteration is far more useful than knowing the formula for a
template.
Answer choice (c)
95% of the students in a class have taken Marketing, 80% have
chosen Finance, 84% have chosen operations (ops), and 90% have
chosen Human Resources (HR). What is the maximum and minimum
percentage of people who have chosen all of the four?