This document summarizes research on developing more secure machine learning classifiers. It discusses how gradient-based and surrogate model approaches can be used to evade existing classifiers. The researchers then propose several techniques for building more robust classifiers, including using infinity-norm regularization, cost-sensitive learning, and modifying kernel parameters. Experiments on handwritten digit and spam filtering datasets show the proposed approaches improve security against evasion attacks compared to standard support vector machines.




![http://pralab.diee.unica.it
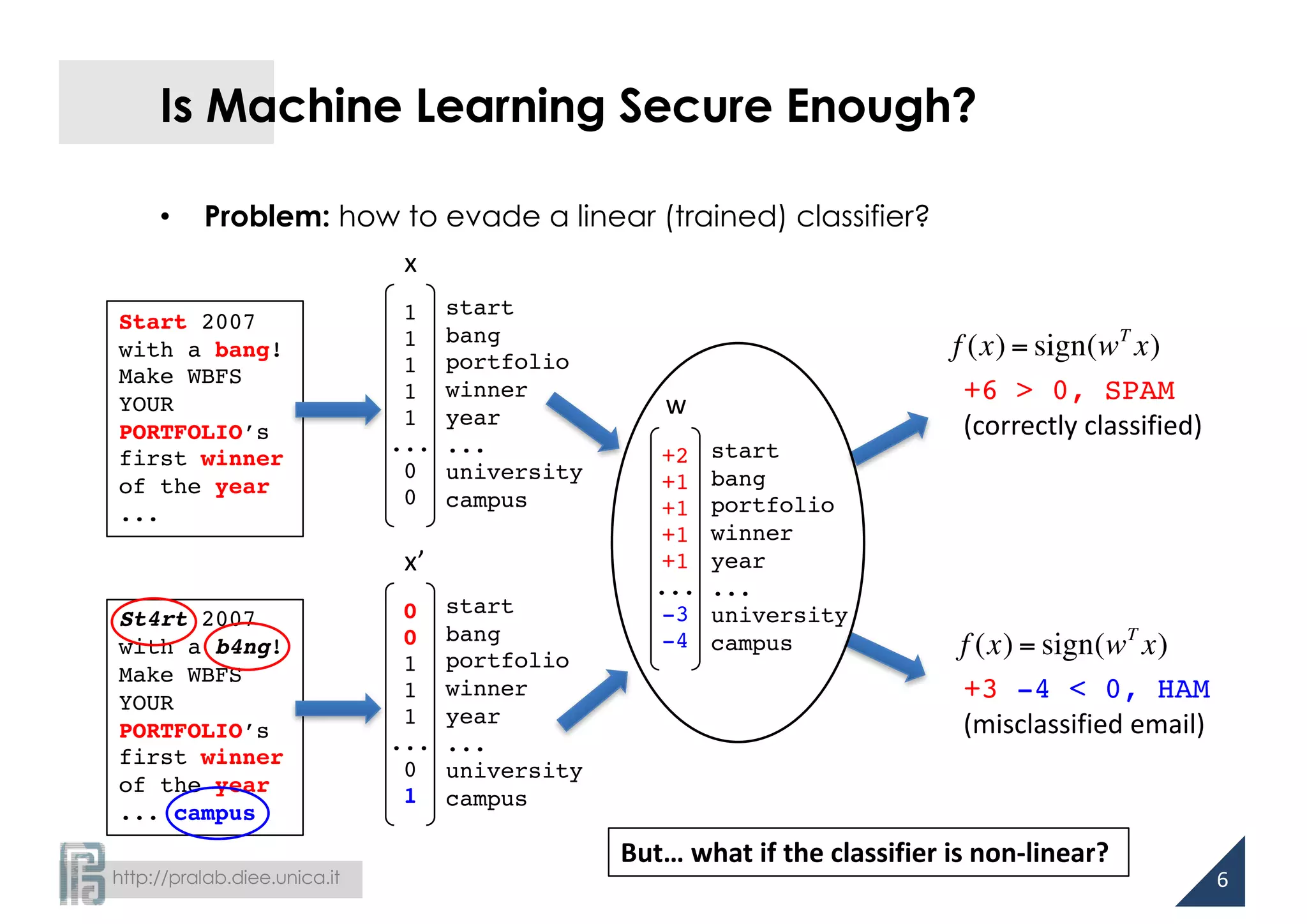
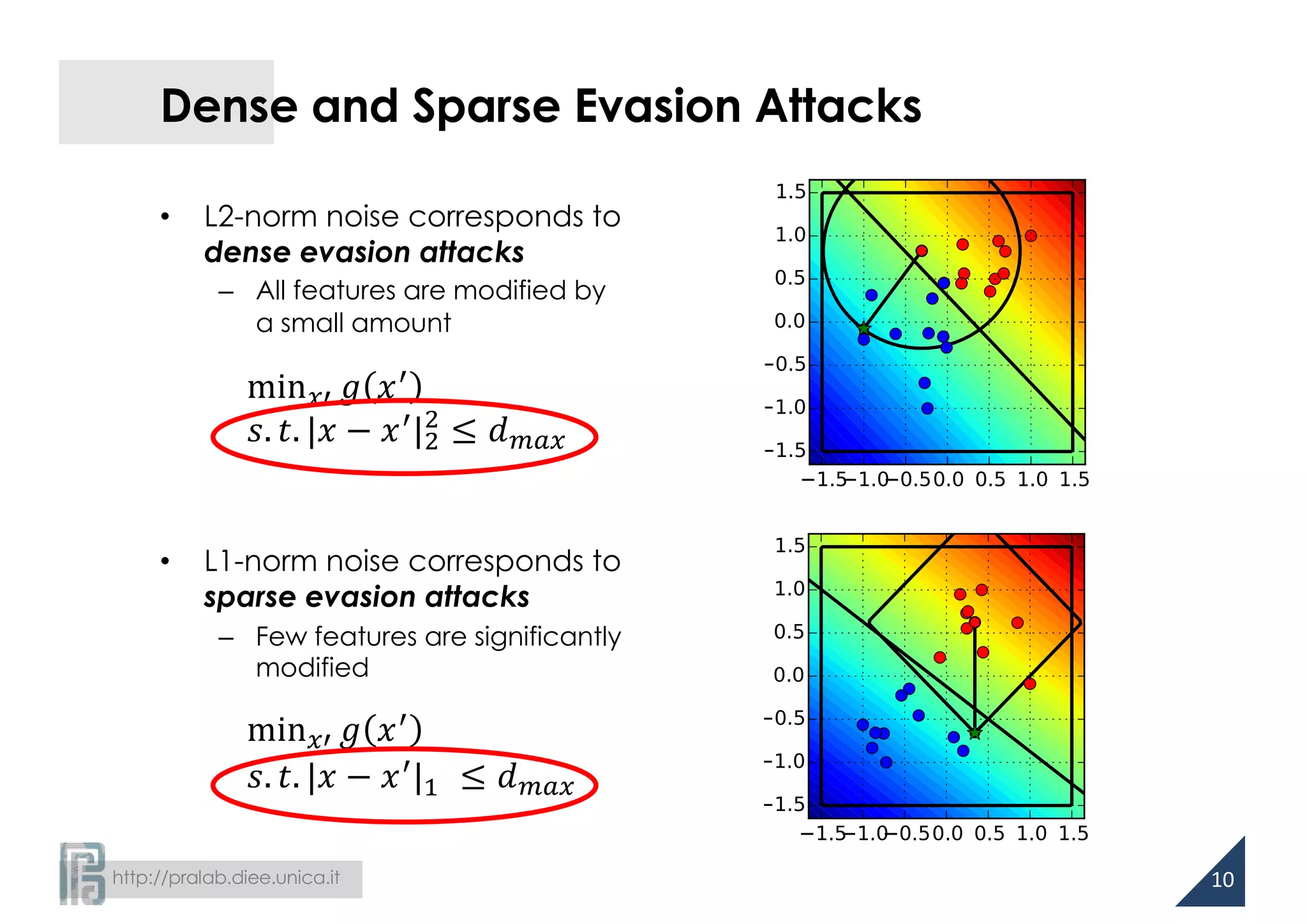
Gradient-based Evasion
• Goal: maximum-confidence evasion
• Attack strategy:
• Non-linear, constrained optimization
– Gradient descent: approximate
solution for smooth functions
• Gradients of g(x) can be analytically
computed in many cases
– SVMs, Neural networks
−2−1.5−1−0.500.51
x
f (x) = sign g(x)( )=
+1, malicious
−1, legitimate
"
#
$
%$
min
x'
g(x')
s.t. d(x, x') ≤ dmax
x '
7
d(x, !x ) ≤ dmax
Feasible domain
[Biggio et al., ECML 2013]](https://image.slidesharecdn.com/biggio16-aisec-oct28-161102091710/75/Secure-Kernel-Machines-against-Evasion-Attacks-7-2048.jpg)
![http://pralab.diee.unica.it
Computing Descent Directions
Support vector machines
Neural networks
x1
xd
d1
dk
dm
xf g(x)
w1
wk
wm
v11
vmd
vk1
……
……
g(x) = αi yik(x,
i
∑ xi )+ b, ∇g(x) = αi yi∇k(x, xi )
i
∑
g(x) = 1+exp − wkδk (x)
k=1
m
∑
#
$
%
&
'
(
)
*
+
,
-
.
−1
∂g(x)
∂xf
= g(x) 1− g(x)( ) wkδk (x) 1−δk (x)( )vkf
k=1
m
∑
RBF kernel gradient: ∇k(x,xi
) = −2γ exp −γ || x − xi
||2
{ }(x − xi
)
8
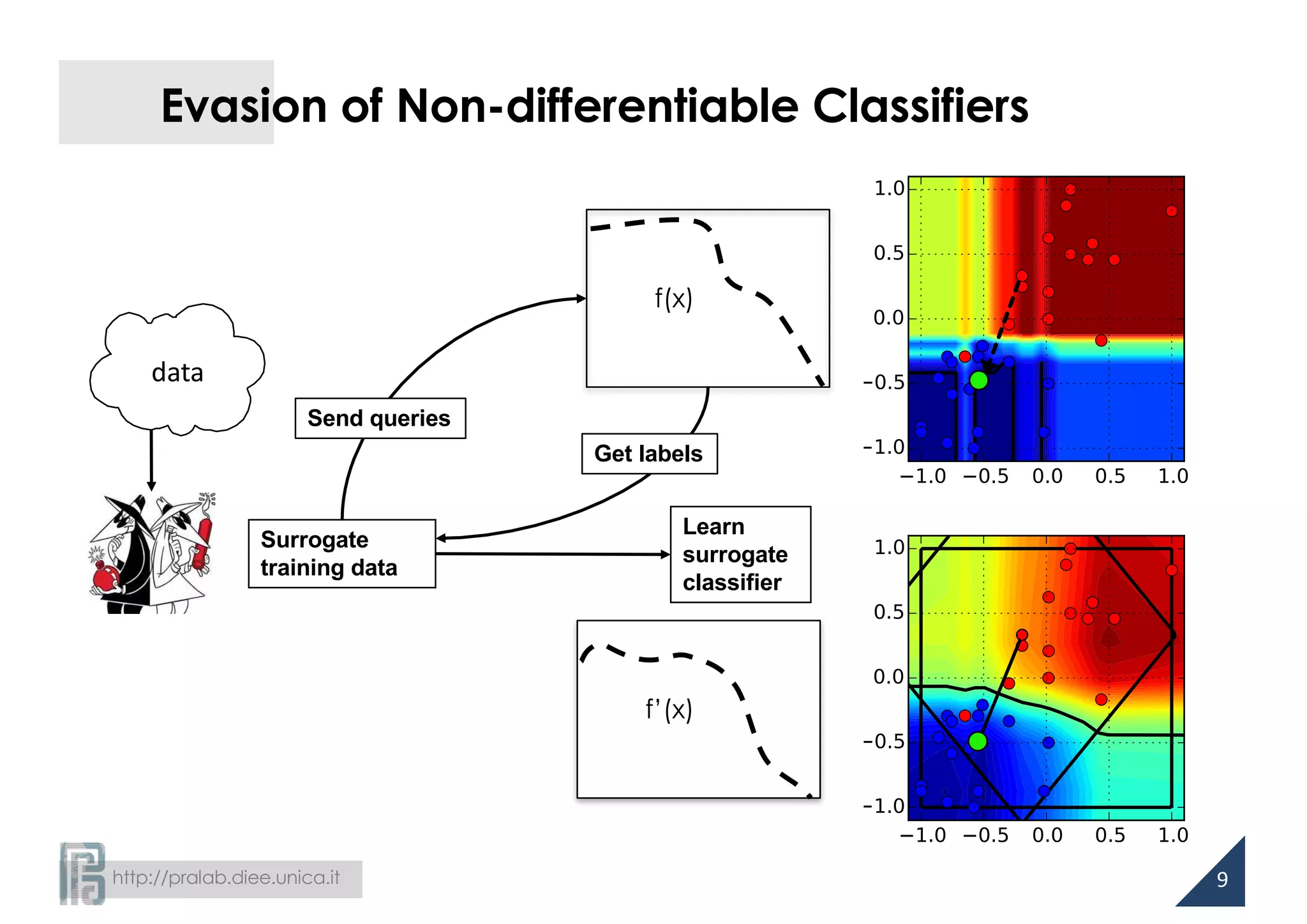
But… what if the classifier is non-differentiable?
[Biggio et al., ECML 2013]](https://image.slidesharecdn.com/biggio16-aisec-oct28-161102091710/75/Secure-Kernel-Machines-against-Evasion-Attacks-8-2048.jpg)


![http://pralab.diee.unica.it
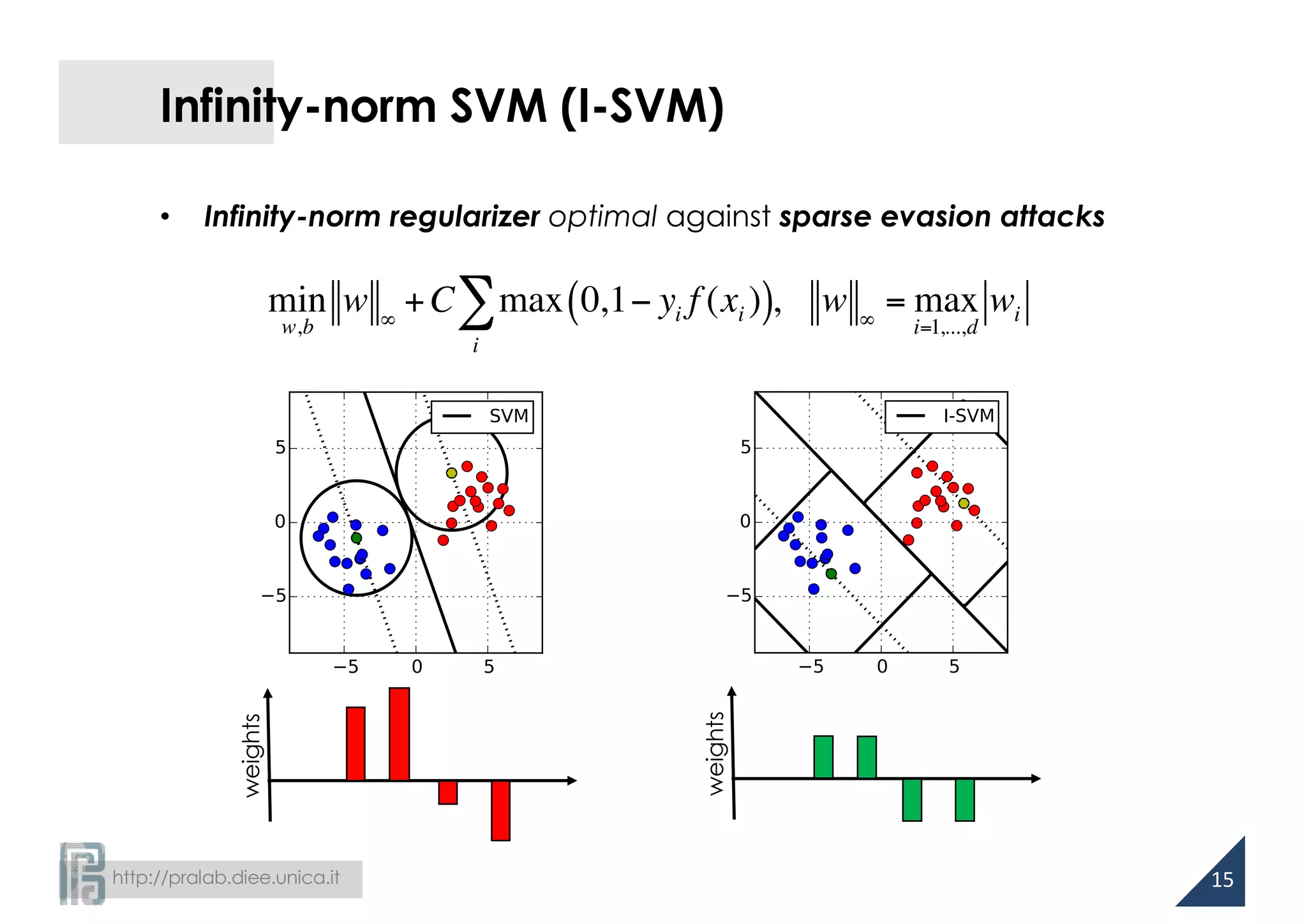
Secure Linear Classifiers
• Intuition in previous work on spam filtering
[Kolcz and Teo, CEAS 2007; Biggio et al., IJMLC 2010]
– the attacker aims to modify few features
– features assigned to highest absolute weights are modified first
– heuristic methods to design secure linear classifiers with more evenly-
distributed weights
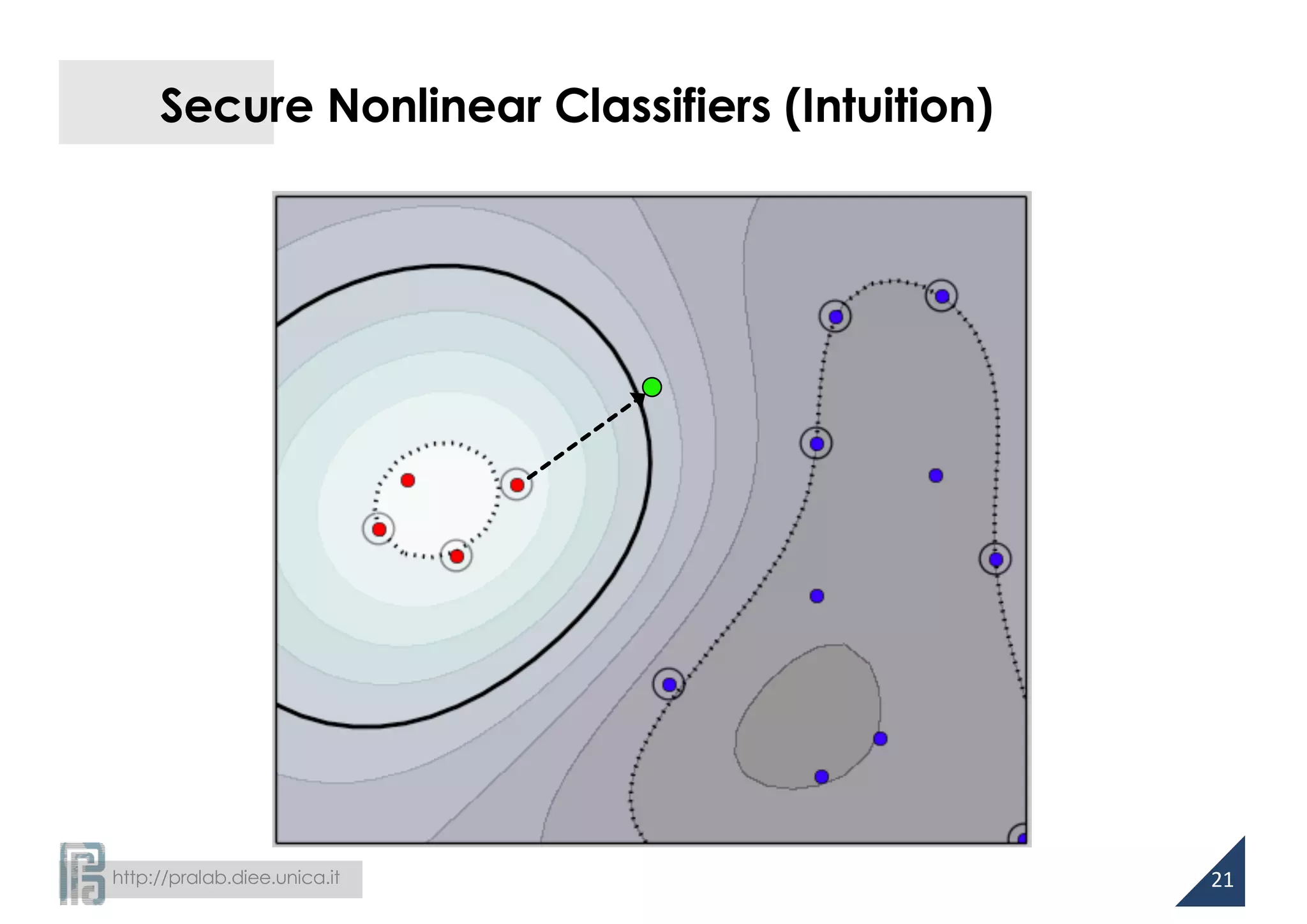
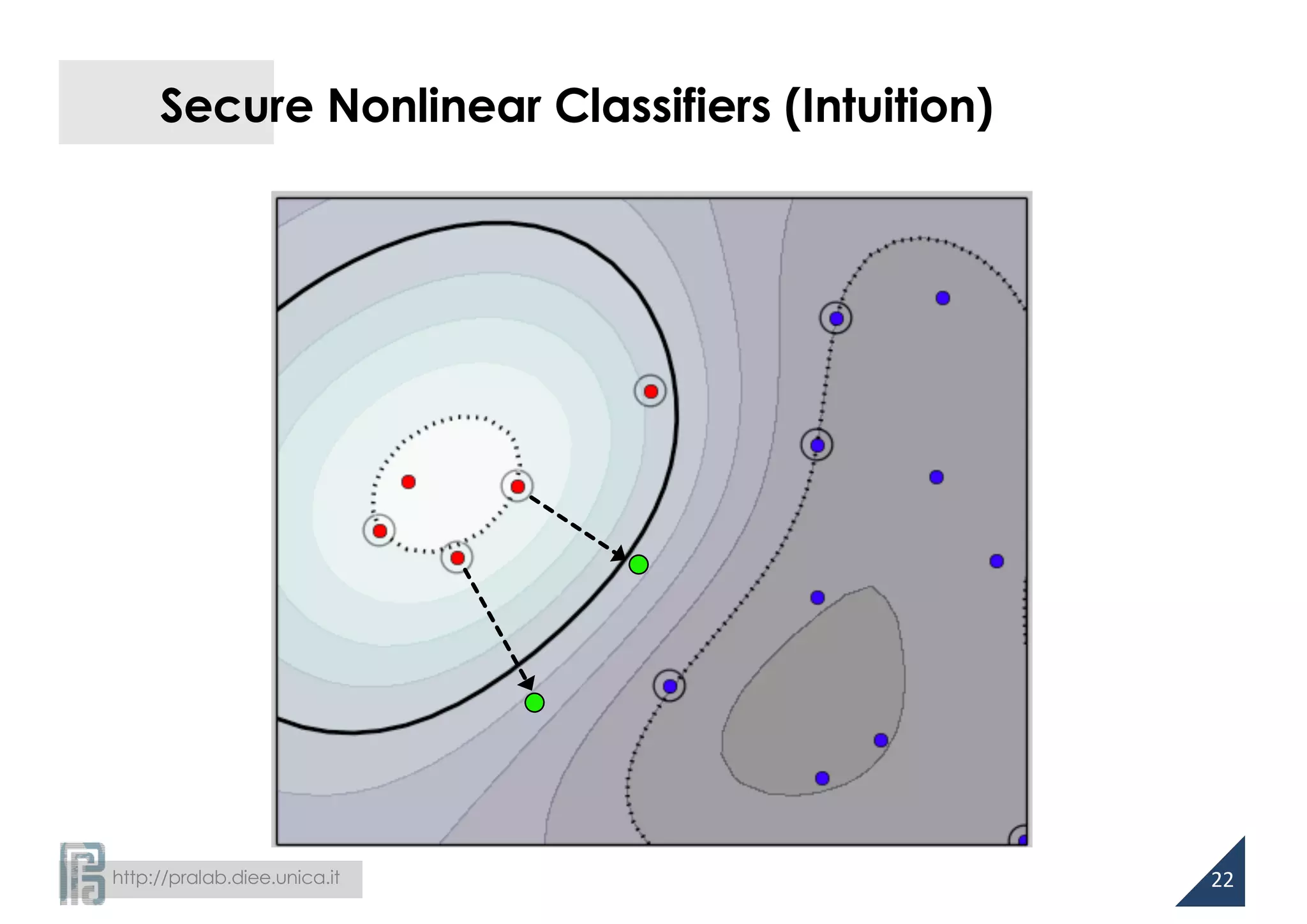
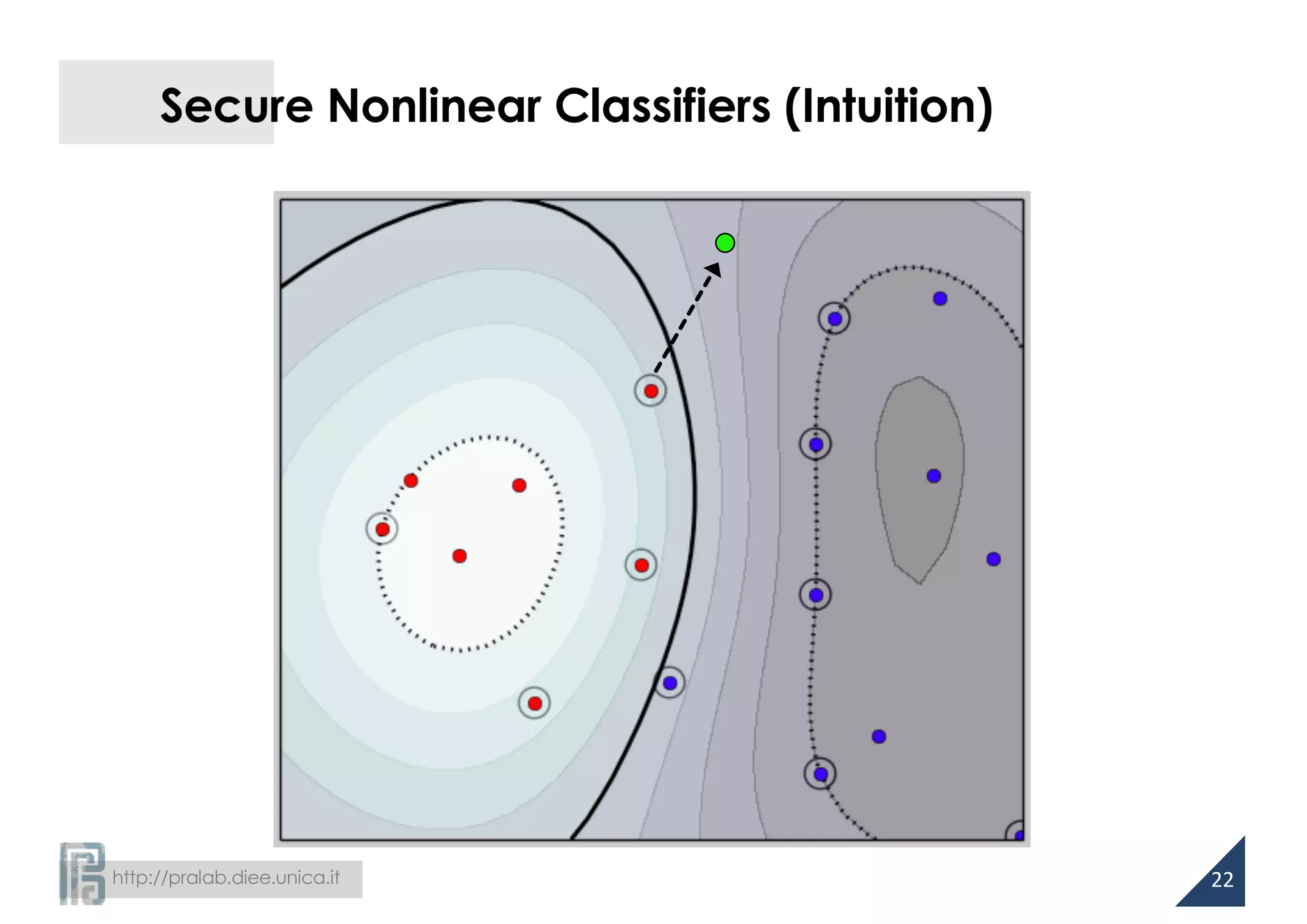
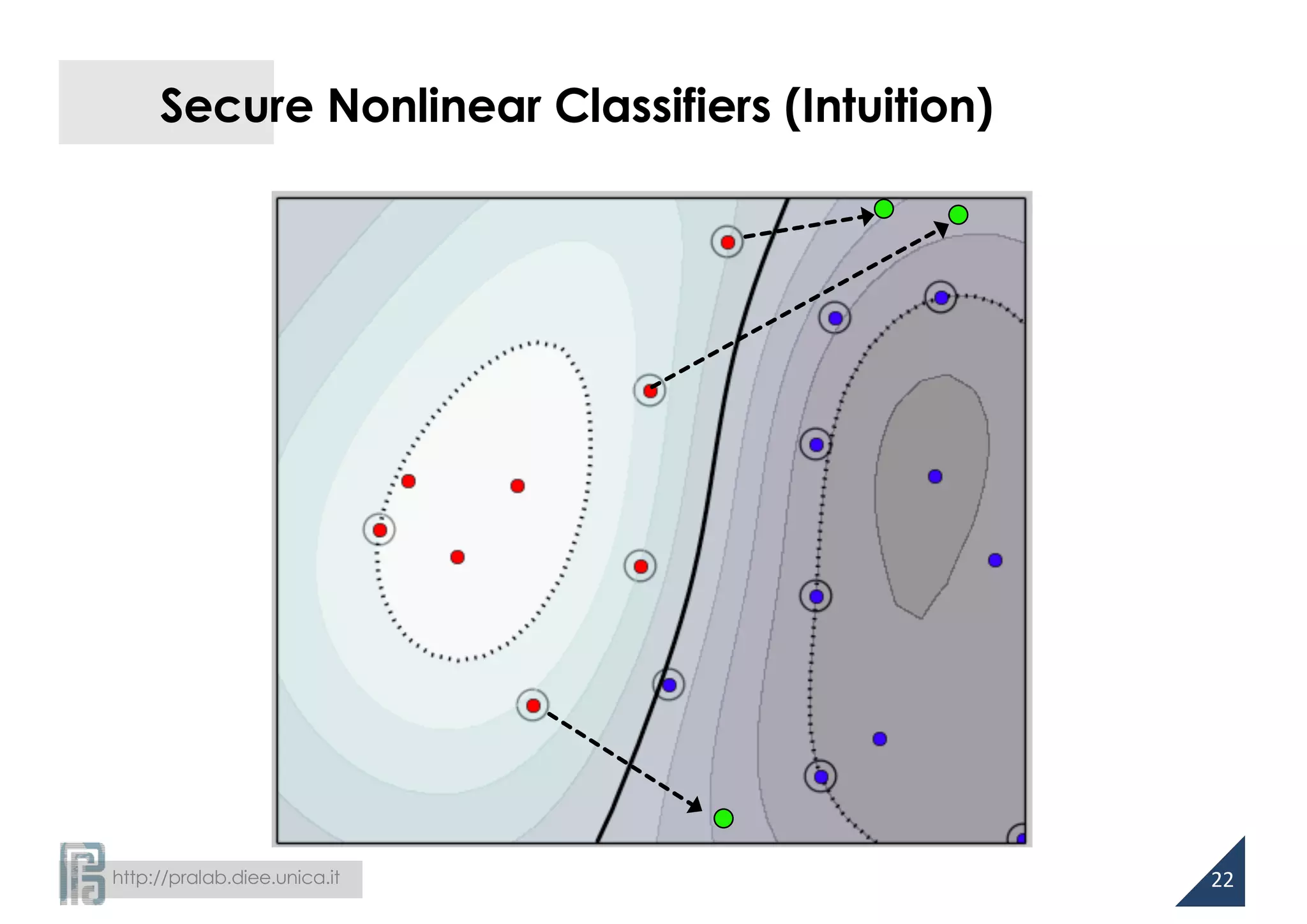
• We know now that the aforementioned attack is sparse
– l1-norm constrained
13
Then, what does more evenly-distributed weights mean
from a more theoretical perspective?](https://image.slidesharecdn.com/biggio16-aisec-oct28-161102091710/75/Secure-Kernel-Machines-against-Evasion-Attacks-13-2048.jpg)
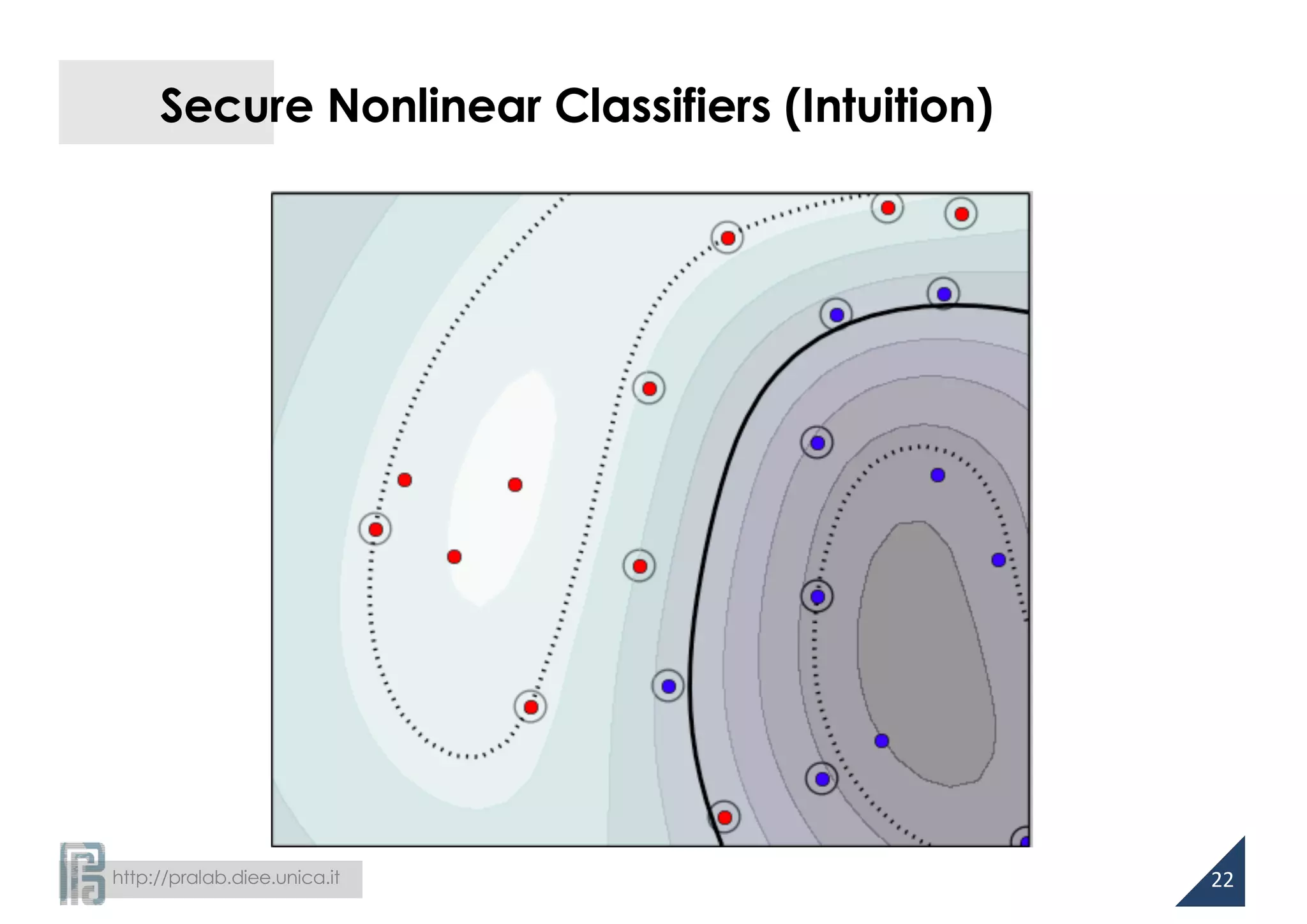
![http://pralab.diee.unica.it
Robustness and Regularization
[Xu et al., JMLR 2009]
• SVM learning is equivalent to a robust optimization problem
– regularization depends on the noise on training data!
14
min
w,b
1
2
wT
w+C max 0,1− yi f (xi )( )
i
∑
min
w,b
max
ui∈U
max 0,1− yi f (xi +ui )( )
i
∑
l2-norm regularization is optimal
against l2-norm noise!
infinity-norm regularization is optimal
against l1-norm noise!](https://image.slidesharecdn.com/biggio16-aisec-oct28-161102091710/75/Secure-Kernel-Machines-against-Evasion-Attacks-14-2048.jpg)
![http://pralab.diee.unica.it
Cost-sensitive Learning
• Unbalancing cost of classification errors to account for different
levels of noise over the training classes
[Katsumada and Takeda, AISTATS ‘15]
• Evasion attacks: higher amount of noise on malicious data
16](https://image.slidesharecdn.com/biggio16-aisec-oct28-161102091710/75/Secure-Kernel-Machines-against-Evasion-Attacks-16-2048.jpg)



![http://pralab.diee.unica.it
• Lux0R [Corona et al., AISec ‘14]
• Adversary’s capability
– adding up to dmax API calls
– removing API calls may
compromise the embedded
malware code
classifier
benign
malicious
API reference
extraction
API reference
selection
learning-based model
runtime analysis
known
label
JavaScript
API references
Suspicious
references
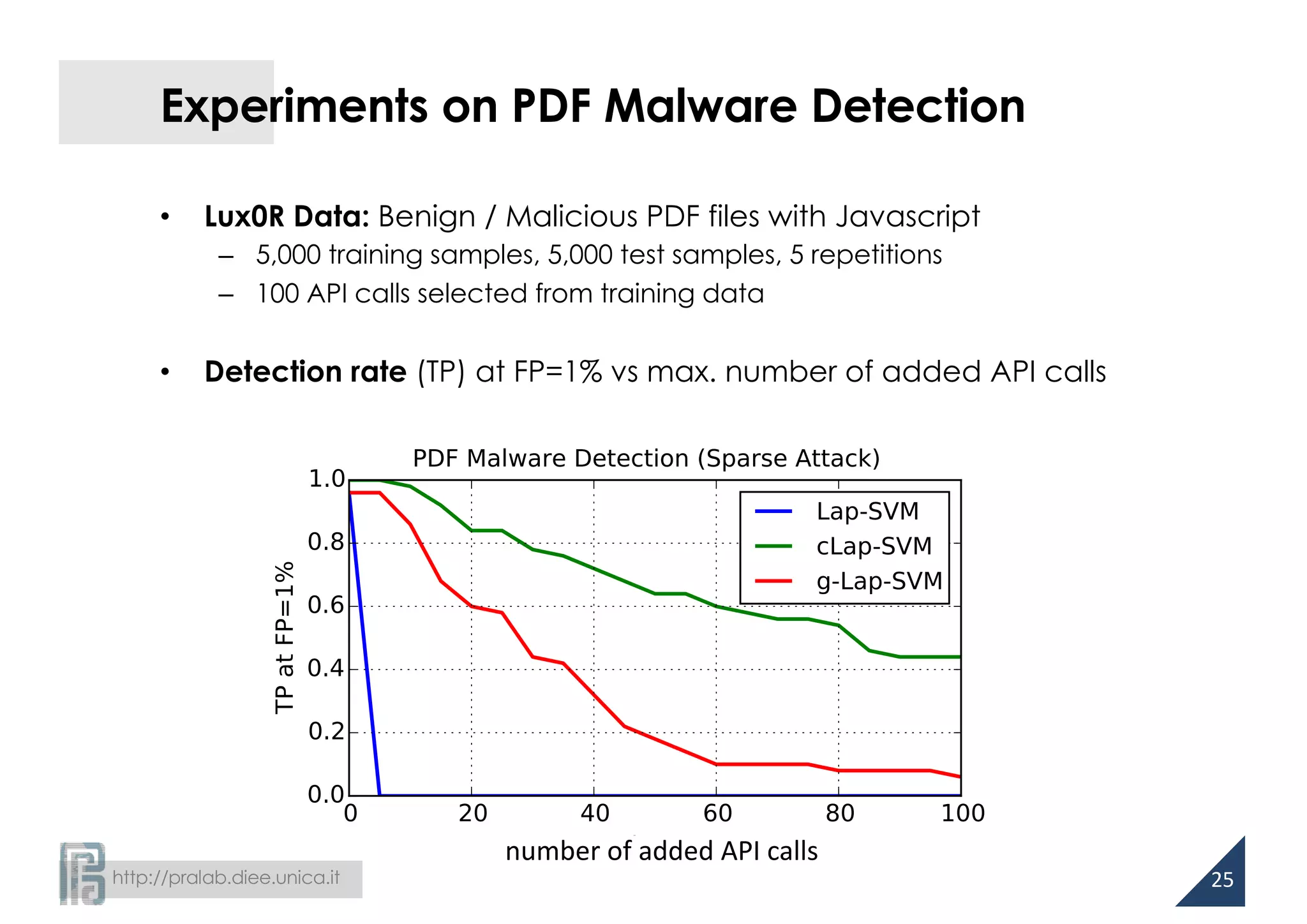
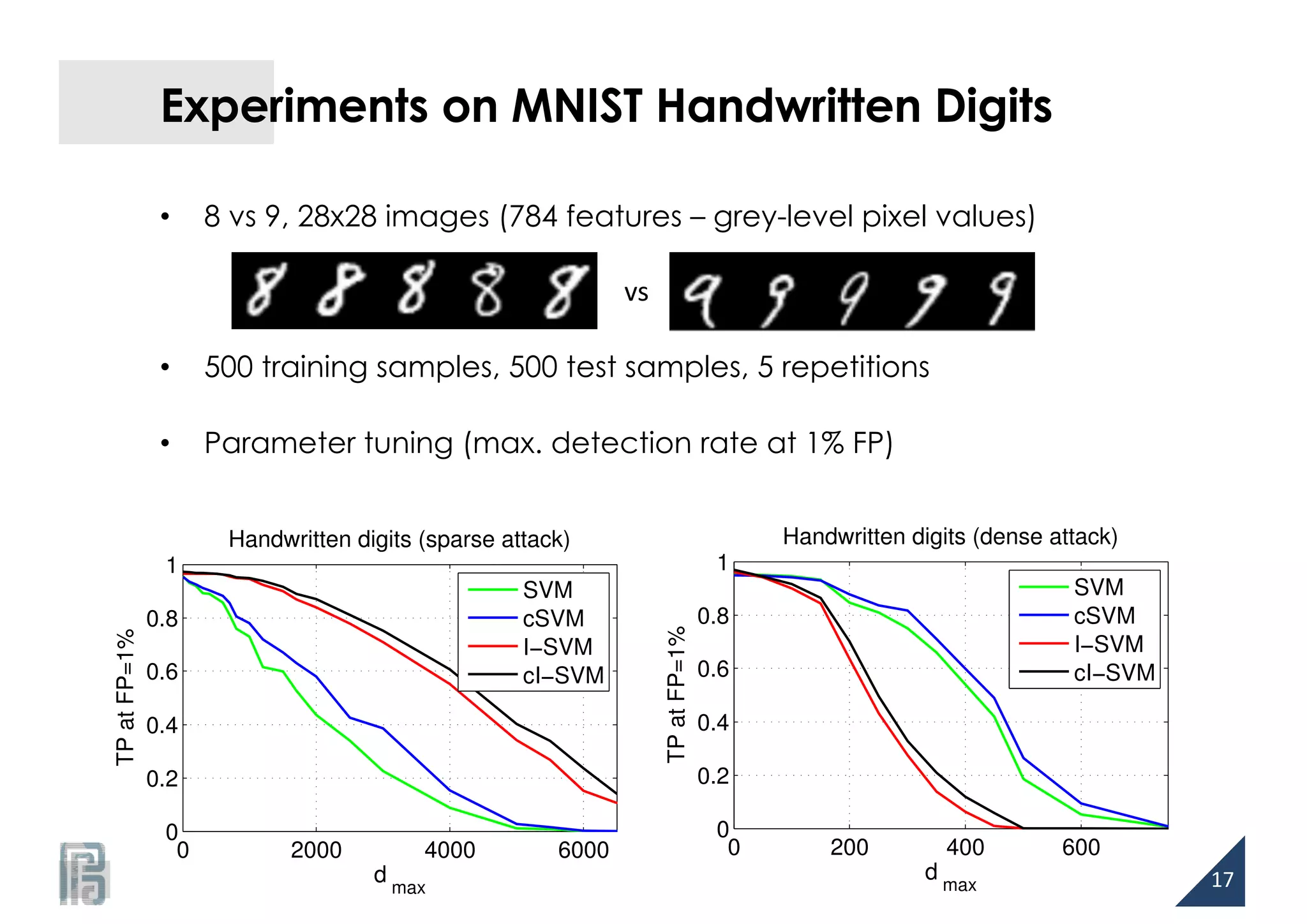
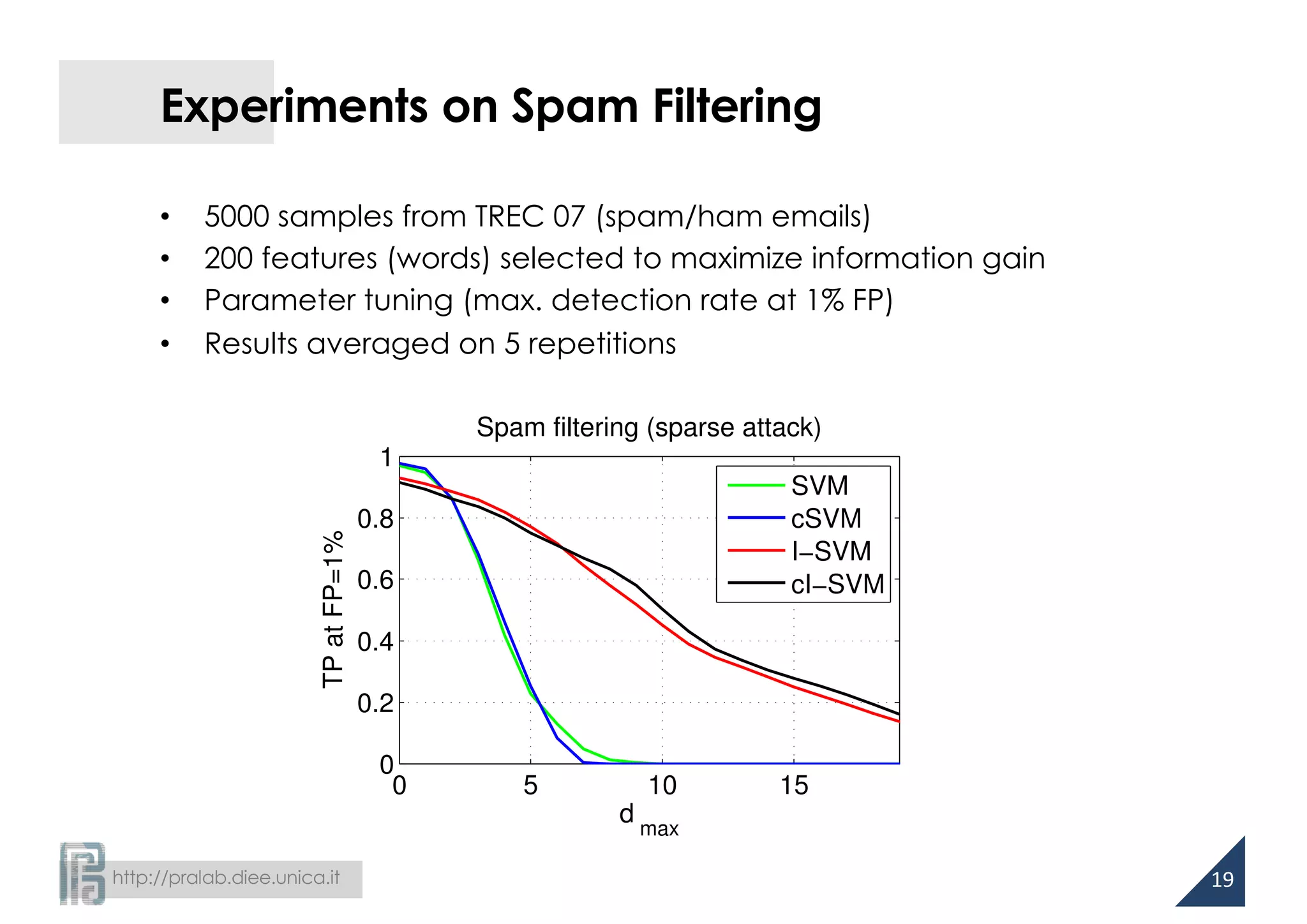
Experiments on PDF Malware Detection
min
x'
g(x')
s.t. d(x, x') ≤ dmax
x ≤ x'
24
eval
isNaN
this.getURL
...](https://image.slidesharecdn.com/biggio16-aisec-oct28-161102091710/75/Secure-Kernel-Machines-against-Evasion-Attacks-27-2048.jpg)