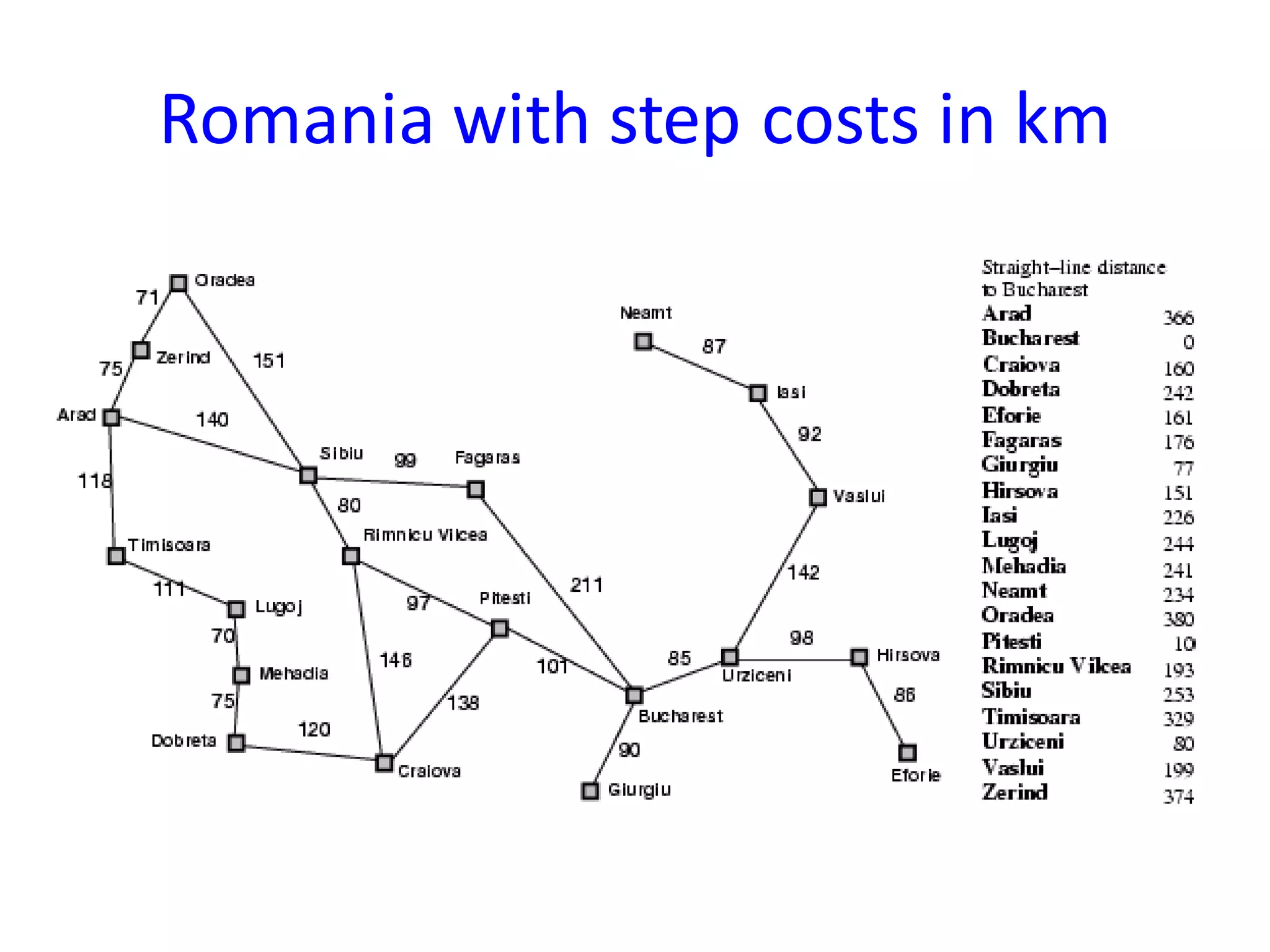
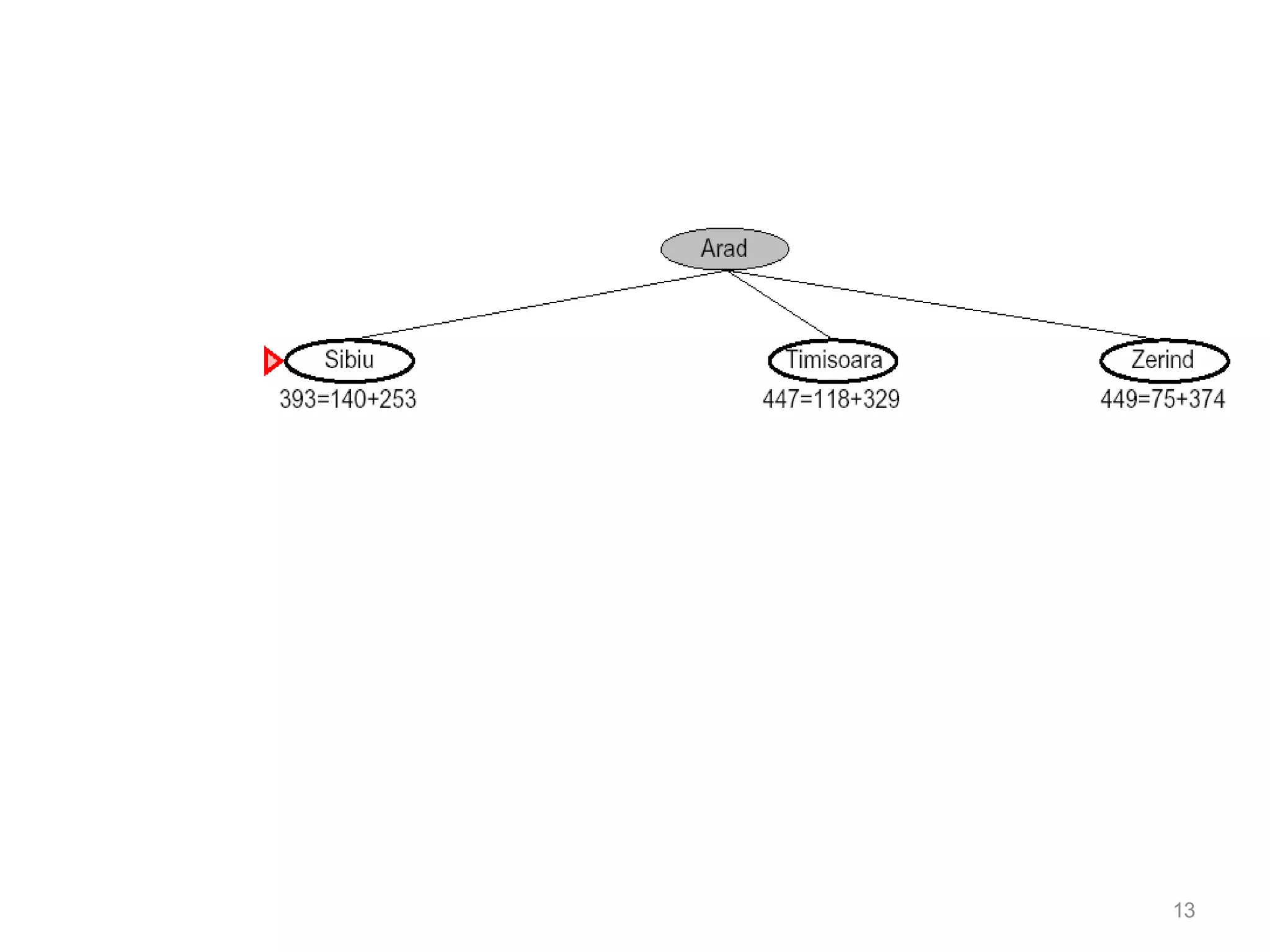
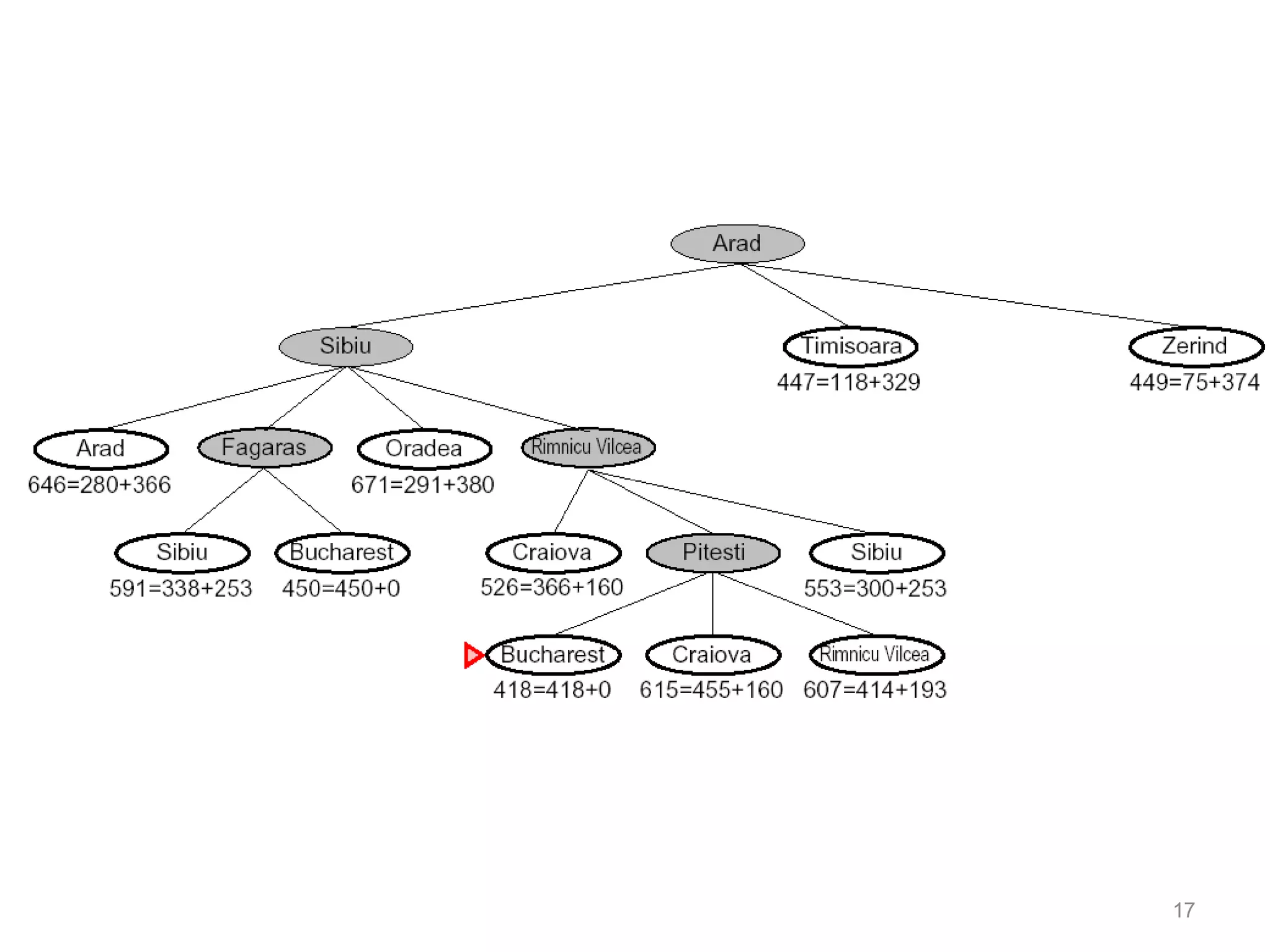
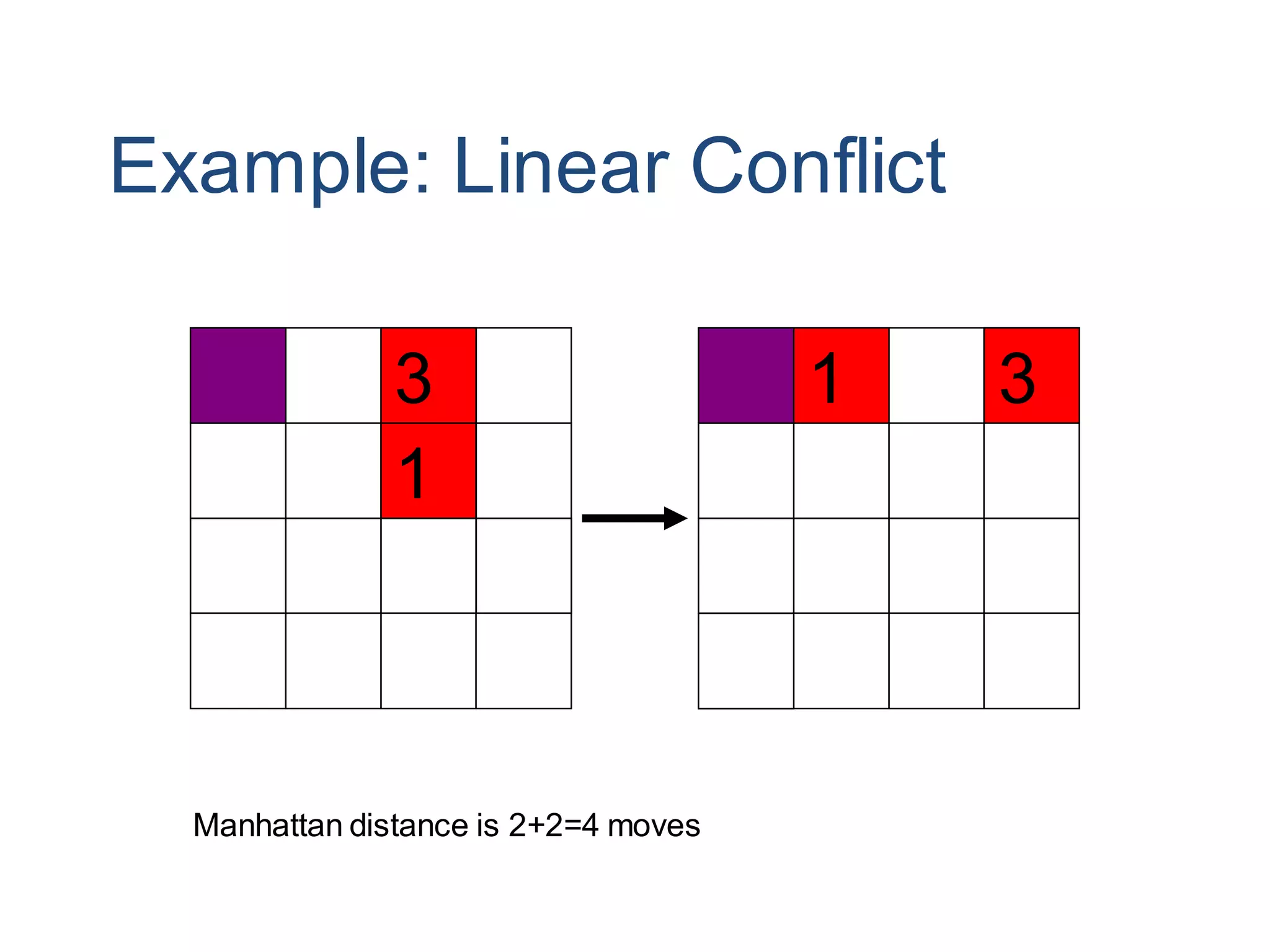
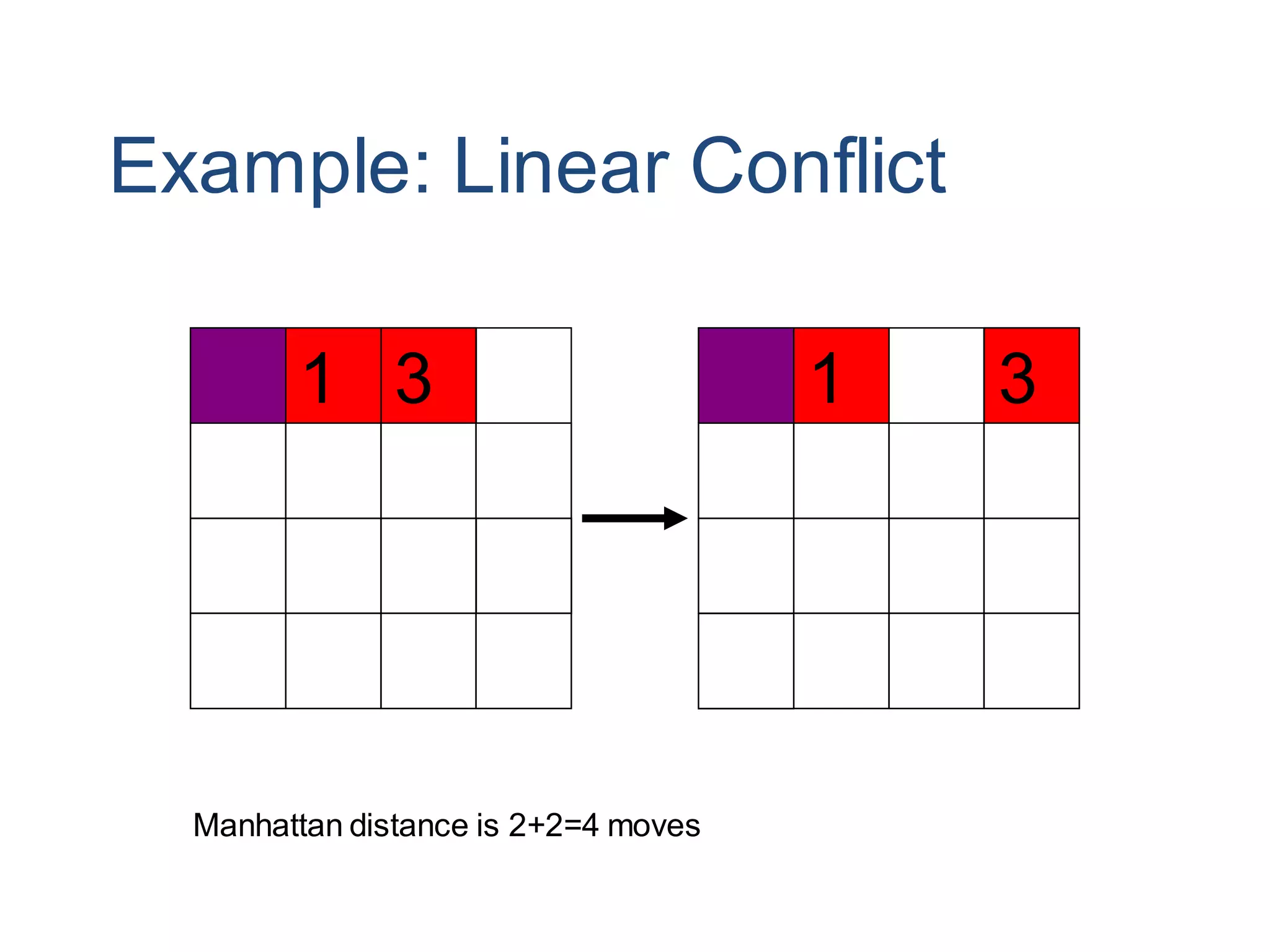
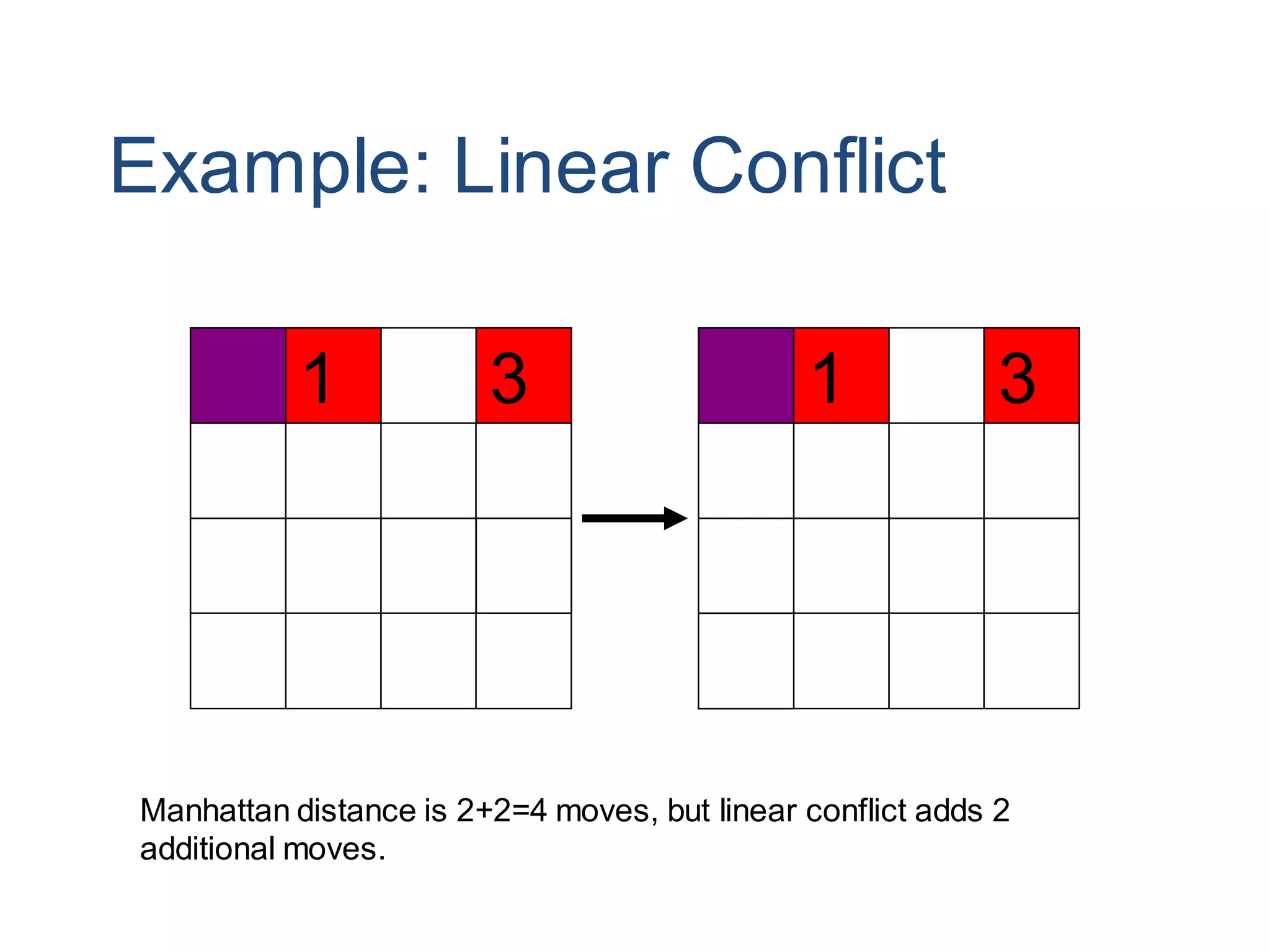
Informed search algorithms aim to be smarter than blind search about which paths to explore by using an evaluation function to estimate the cost to the goal for each node, with best-first search always expanding the node with the lowest estimated cost; A* search combines the cost so far and estimated remaining cost to provide an optimal search when the heuristic is admissible or consistent; pattern database heuristics derive more accurate estimates of moves required by solving subproblems exactly and combining the solutions.

1. Informed search algorithms
Chapter 3
(Based on Slides by Stuart Russell,
Richard Korf and UW-AI faculty)

2. 2
Informed (Heuristic) Search
Idea: be smart
about what paths
to try.

3. 3
Blind Search vs. Informed Search
• What’s the difference?
• How do we formally specify this?
A node is selected for expansion based on an
evaluation function that estimates cost to goal.

4. 4
General Tree Search Paradigm
function tree-search(root-node)
fringe  successors(root-node)
while ( notempty(fringe) )
{node  remove-first(fringe)
state  state(node)
if goal-test(state) return solution(node)
fringe  insert-all(successors(node),fringe) }
return failure
end tree-search

5. 5
General Graph Search Paradigm
function tree-search(root-node)
fringe  successors(root-node)
explored  empty
while ( notempty(fringe) )
{node  remove-first(fringe)
state  state(node)
if goal-test(state) return solution(node)
fringe  insert-all(successors(node),fringe, if node not in explored)
explored  insert(node,explored)
}
return failure
end tree-search

6. 6
Best-First Search
• Use an evaluation function f(n) for node n.
• Always choose the node from fringe that has
the lowest f value.
3 5 1
4 6

7. Best-first search
• A search strategy is defined by picking the order of node
expansion
• Idea: use an evaluation function f(n) for each node
– estimate of "desirability“
Expand most desirable unexpanded node
• Implementation:
Order the nodes in fringe in decreasing order of desirability
• Special cases:
– greedy best-first search
– A* search

8. Romania with step costs in km

9. Greedy best-first search
• Evaluation function f(n) = h(n) (heuristic)
= estimate of cost from n to goal
• e.g., hSLD(n) = straight-line distance from n to
Bucharest
• Greedy best-first search expands the node
that appears to be closest to goal

10. Properties of greedy best-first search
• Complete?
• No – can get stuck in loops, e.g., Iasi  Neamt  Iasi 
Neamt 
• Time?
• O(bm),but a good heuristic can givedramatic
improvement
• Space?
• O(bm) -- keeps all nodes in memory
• Optimal?
• No

11. A* search
• Idea: avoid expanding paths that are already
expensive
• Evaluation function f(n) = g(n) + h(n)
• g(n) = cost so far to reach n
• h(n) = estimated cost from n to goal
• f(n) = estimated total cost of path through n to
goal

12. 12
A* for Romanian Shortest Path

13. 13

14. 14

15. 15

16. 16

17. 17

18. Admissible heuristics
• A heuristic h(n) is admissible if for every node n,
h(n) ≤ h*(n), whereh*(n) is the true cost to reach the goal state from
n.
• An admissible heuristic neveroverestimates thecost to reach the
goal, i.e., it is optimistic
• Example: hSLD(n) (never overestimatestheactual road distance)
• Theorem: If h(n) is admissible, A* using TREE-SEARCH isoptimal

19. Consistent Heuristics
• h(n) is consistentif
– for every node n
– for every successor n´ due to legal action a
– h(n) <= c(n,a,n´) + h(n´)
• Every consistentheuristicis also admissible.
• Theorem:If h(n) is consistent,A* using GRAPH-
SEARCHis optimal
19
n
n´ G
c(n,a,n´)
h(n´)
h(n)

20. Properties of A*
• Complete?
Yes (unless there are infinitely many nodes with f ≤ f(G) )
• Time? Exponential
• Space? Keeps all nodes in memory
• Optimal?
Yes (depending upon search algo and heuristic property)
http://www.youtube.com/watch?v=huJEgJ82360

21. Admissible heuristics
E.g., for the 8-puzzle:
• h1(n) = number of misplaced tiles
• h2(n) = total Manhattan distance
(i.e., no. of squares from desired location of each tile)
• h1(S) = ?
• h2(S) = ?

22. Admissible heuristics
E.g., for the 8-puzzle:
• h1(n) = number of misplaced tiles
• h2(n) = total Manhattan distance
(i.e., no. of squares from desired location of each tile)
• h1(S) = ? 8
• h2(S) = ? 3+1+2+2+2+3+3+2 = 18

23. Dominance
• If h2(n) ≥ h1(n) for all n (both admissible)
then h2 dominates h1
• h2 is better for search
• Typicalsearch costs (average number of node expanded):
• d=12 IDS = 3,644,035 nodes
A*(h1) = 227 nodes
A*(h2) = 73 nodes
• d=24 IDS = too many nodes
A*(h1) = 39,135 nodes
A*(h2) = 1,641 nodes

24. Relaxed problems
• A problem with fewer restrictions on the actions is called a
relaxed problem
• The cost of an optimal solution to a relaxed problem is an
admissible heuristic for the original problem
• If the rules of the 8-puzzle are relaxed so that a tile can move
anywhere, then h1(n) gives the shortest solution
• If the rules are relaxed so that a tile can move to any adjacent
square, then h2(n) gives the shortest solution

25. Memory Problem?
• Iterative deepening A*
– Similar to ID search

26. Non-optimal variations
• Use more informative, but inadmissible
heuristics
• Weighted A*
– f(n) = g(n)+ w.h(n) where w>1
– Typically w=5.
– Solution quality bounded by w for admissible h

27. Sizes of Problem Spaces
• 8 Puzzle: 105 .01 seconds
• 23 Rubik’s Cube: 106 .2 seconds
• 15 Puzzle: 1013 6 days
• 33 Rubik’s Cube: 1019 68,000 years
• 24 Puzzle: 1025 12 billion years
Brute-Force SearchTime (10 million
nodes/second)
Problem Nodes

28. Performance of IDA* on 15 Puzzle
• Random 15 puzzle instances were first solved
optimally using IDA* with Manhattan distance
heuristic (Korf, 1985).
• Optimal solution lengths average 53 moves.
• 400 million nodes generated on average.
• Average solution time is about 50 seconds on
current machines.

29. Limitation of Manhattan Distance
• To solve a 24-Puzzle instance, IDA* with
Manhattan distance would take about 65,000
years on average.
• Assumes that each tile moves independently
• In fact, tiles interfere with each other.
• Accounting for these interactions is the key to
more accurate heuristic functions.

30. Example: Linear Conflict
1 3
3 1
Manhattan distance is 2+2=4 moves

31. Example: Linear Conflict
1 3
3 1
Manhattan distance is 2+2=4 moves

32. Example: Linear Conflict
1 3
3
1
Manhattan distance is 2+2=4 moves

33. Example: Linear Conflict
1 3
3
1
Manhattan distance is 2+2=4 moves

34. Example: Linear Conflict
1 3
3
1
Manhattan distance is 2+2=4 moves

35. Example: Linear Conflict
1 3
3
1
Manhattan distance is 2+2=4 moves

36. Example: Linear Conflict
1 3
3
1
Manhattan distance is 2+2=4 moves, but linear conflict adds 2
additional moves.

37. Linear Conflict Heuristic
• Hansson, Mayer, and Yung, 1991
• Given two tiles in their goal row, but reversed
in position, additional vertical moves can be
added to Manhattan distance.
• Still not accurate enough to solve 24-Puzzle
• We can generalize this idea further.

38. More Complex Tile Interactions
3
7
11
12 13 14 15
14 7
3
15 12
11 13
M.d. is 19 moves, but 31 moves are
needed.
M.d. is 20 moves, but 28 moves are
needed
3
7
11
12 13 14 15
7 13
12
15 3
11 14
M.d. is 17 moves, but 27 moves are
needed
3
7
11
12 13 14 15
12 11
7 14
13 3
15

39. Pattern Database Heuristics
• Culberson and Schaeffer, 1996
• A pattern database is a complete set of such
positions, with associated number of moves.
• e.g. a 7-tile pattern database for the Fifteen
Puzzle contains 519 million entries.

40. Heuristics from Pattern Databases
1 2 3
4 5 6 7
8 9 10 11
12 13 14 15
5 10 14 7
8 3 6 1
15 12 9
2 11 4 13
31 moves is a lower bound on the total number of moves needed to solve
this particular state.

41. Combining Multiple Databases
1 2 3
4 5 6 7
8 9 10 11
12 13 14 15
5 10 14 7
8 3 6 1
15 12 9
2 11 4 13
Overall heuristic is maximum of 31 moves
31 moves needed to solve red tiles
22 moves need to solve blue tiles

42. Additive Pattern Databases
• Culberson and Schaeffer counted all moves
needed to correctly position the pattern tiles.
• In contrast, we count only moves of the
pattern tiles, ignoring non-pattern moves.
• If no tile belongs to more than one pattern,
then we can add their heuristic values.
• Manhattan distance is a special case of this,
where each pattern contains a single tile.

43. Example Additive Databases
1 2 3
4 5 6 7
8 9 10 11
12 13 15 14
The 7-tile database contains 58 million entries. The 8-tile database contains
519 million entries.

44. Computing the Heuristic
1 2 3
4 5 6 7
8 9 10 11
12 13 14 15
5 10 14 7
8 3 6 1
15 12 9
2 11 4 13
Overall heuristic is sum, or 20+25=45 moves
20 moves needed to solve red tiles
25 moves needed to solve blue tiles

45. Performance on 15 Puzzle
• IDA* with a heuristic based on these additive
pattern databases can optimally solve random
15 puzzle instances in less than 29
milliseconds on average.
• This is about 1700 times faster than with
Manhattan distance on the same machine.

46. Assignment 1
• Flashlight Problem
• Do not use pattern database heuristics