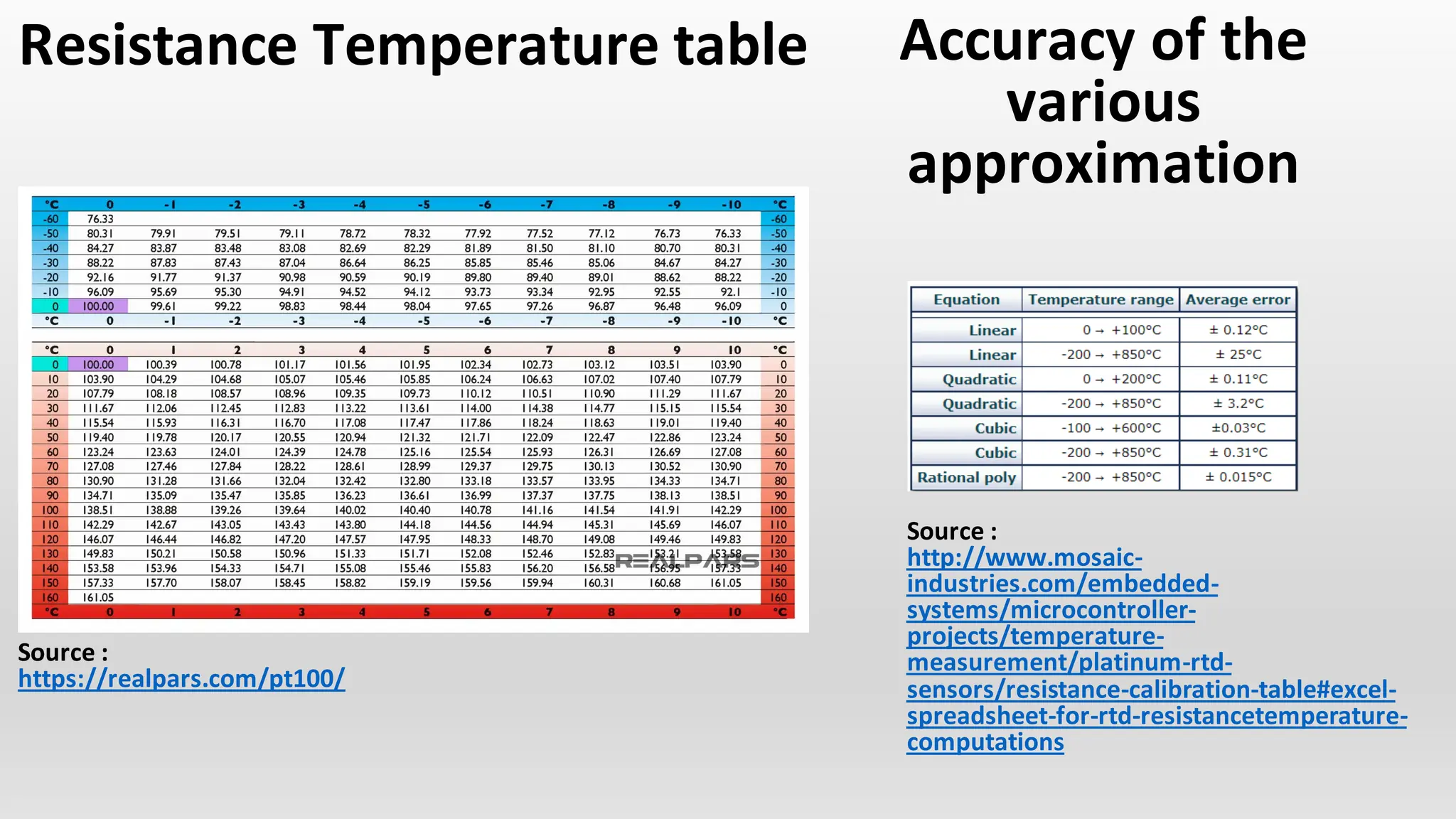
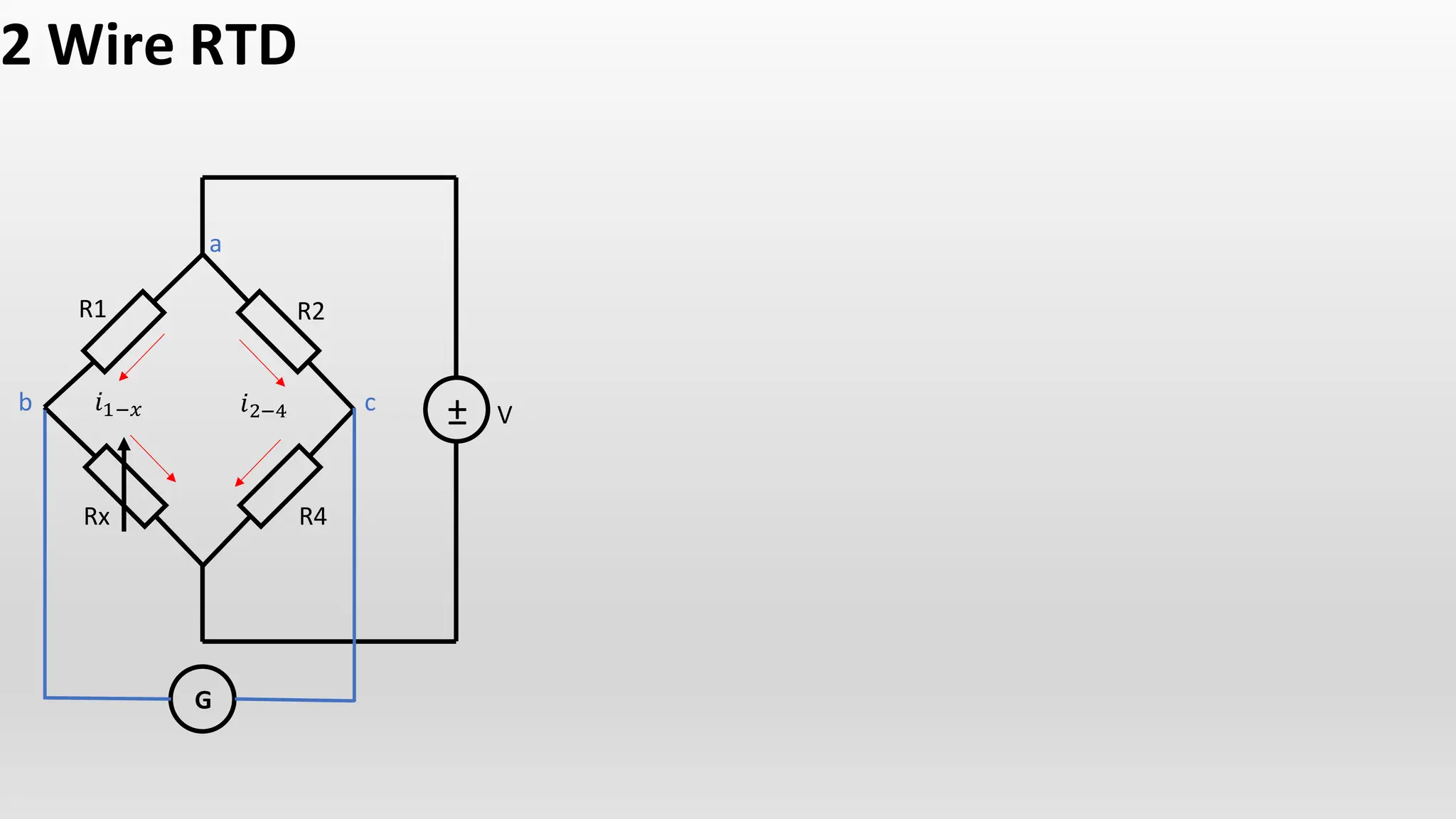
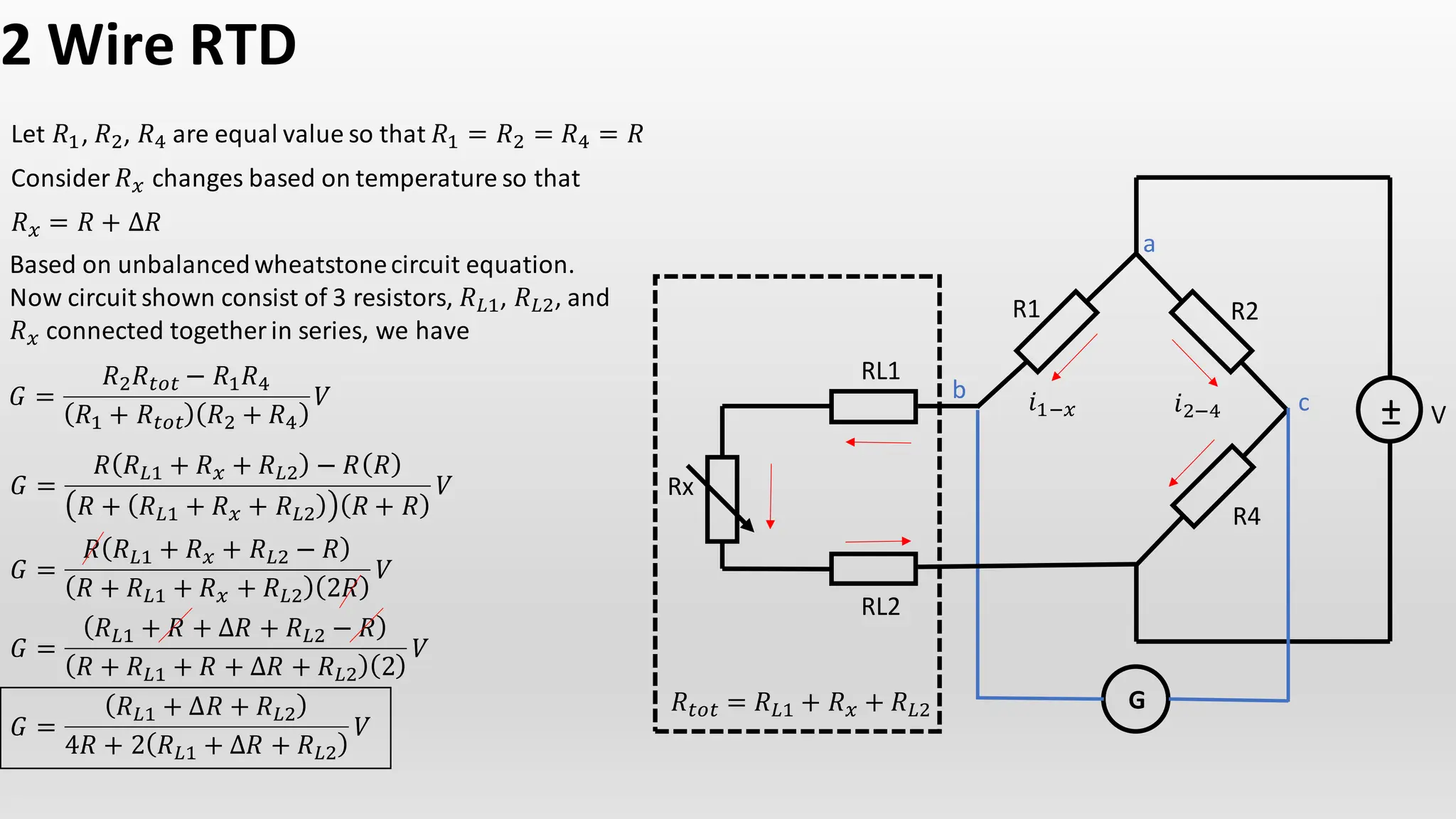
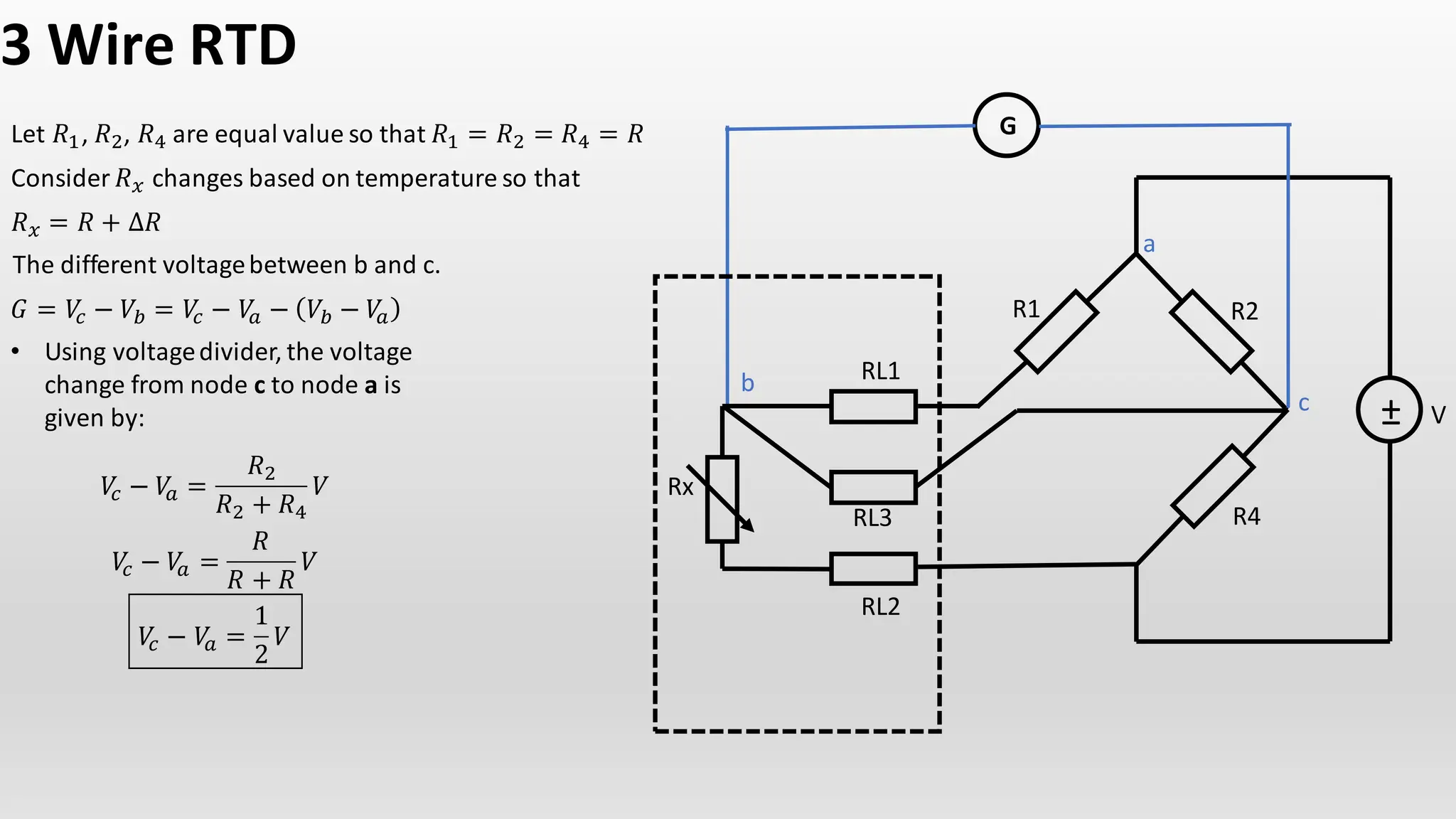
The document discusses the characteristics and calculations of resistance temperature detectors (RTDs), particularly the PT100 type. It outlines the relationship between resistance and temperature using equations and describes the construction and function of a Wheatstone bridge circuit in relation to RTDs. Additionally, it includes details on voltage changes in balanced and unbalanced conditions of the circuit.