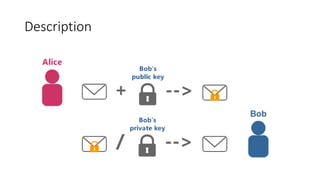
This document describes the RSA encryption algorithm. It explains that RSA was first described publicly in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman. It then provides the steps of the RSA algorithm, including choosing two prime numbers to generate the public and private keys, and using modular exponentiation and the private key to encrypt and decrypt messages. The document concludes by working through an example of Alice and Bob using RSA to encrypt and decrypt a message.

1. RSA algorithm
Vo Tinh Thuong
votinhthuong9@gmail.com

2. RSA algorithm
Ron Rivest, Adi Shamir, and Leonard Adleman, who first publicly
described the algorithm in 1977.

3. Algorithm
1. n = pq, where p and q are distinct primes.
2. phi, φ = (p-1)(q-1)
3. e < n such that gcd(e, phi)=1
4. c = 𝑚 𝑒
mod n, 1<m<n.
5. d = 𝑒−1
mod phi.
6. m = 𝑐 𝑑
mod n.

4. Description

5. Demonstrate
Alice choose p = 17 and q = 11
=> N = p * q = 187
Φ = (p-1)(q-1) = 160
e = 7
=> Public key: N and e

6. Bob want to send a kiss, it’s mean X in English. So
he find DEX of X in ASCII, and get value equal 88.

7. Bob do:
c = 𝑚 𝑒
mod n = 887
mod 187 = 11
then send back that value to Alice
=> Eve can catch (sniff) it but can’t reverse it!

8. Alice use function:
d = 𝑒−1
mod phi = 23

9. ?!

10. Extended Euclidean algorithm

11. e * d mod φ = 1
7 * d mod 160 = 1
160𝑥 + 7𝑦 = 1
160 = 10(7) + 90
7 = 0(90) + 7
90 = 10(7) + 20
7 = 0(20) + 7
20 = 2(7) + 6
7 = 1(6) + 1

12. 1 = 7 – 1(6)
1 = 7 – 1(20 – 2(7))
1 = 3(7) – 1(20)
1 = 3(7) – 1(90 – 10(70))
1 = 13(7) – 1(90)
1 = 13(7) – 1(160 – 10(7))
1 = 23(7) – 1(160)
e * d mod φ = 1
7 * d mod 160 = 1
160𝑥 + 7𝑦 = 1
160 = 10(7) + 90
7 = 0(90) + 7
90 = 10(7) + 20
7 = 0(20) + 7
20 = 2(7) + 6
7 = 1(6) + 1

13. First love give all for you
Finally… After all this time? Always!
m = 𝑐 𝑑
mod n = 1123
mod 187 = 88
88 => DEX of ASCII => ‘X’ character
=> It’s mean kiss from Bob to Alice.
Eve lie down, try not to cry, cry a lot =)))

14. THE END!