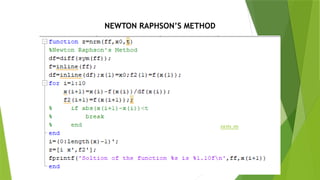
The document outlines numerical methods for finding roots of functions, specifically focusing on the method of false position and Newton-Raphson method. It includes MATLAB code snippets for implementing these algorithms and provides parameters for execution. The document concludes by referring to an attached function for the Newton-Raphson method.

3. clear;clc;
%ff='x^3-2*x-5';
%ff='cos(x)-x*exp(x)'
%ff='x*log10(x)-1.2'
ff='x^4-32'
a=2;b=3;
% Method of False Position or Regula False Method
f=inline(ff);k=1;i=1;x=[];
while i<10
c=a-(b-a)*f(a)/(f(b)-f(a));d=c;a1=a;b1=b;
if f(a)*f(c)<0
b=c;
else
a=c;
end
x=[x;i a1 f(a1) b1 f(b1) d f(d)];
i=i+1;
end
fprintf('%gt %1.5ft %1.5ft %1.5ft %1.5ft %1.5ft %1.5ftn',x')
fprintf('Approximate solution of %s = 0 is %1.5fn',ff,d)
FALSE POSITION METHOD
False Position Method

4. FALSE POSITION METHOD

5. function root = newtonRaphson(func, dfunc, x0, tol, maxIter)
% func: function handle of f(x)
% dfunc: derivative of f(x) (function handle)
% x0: initial guess
% tol: tolerance for stopping criterion
% maxIter: maximum number of iterations
end
Complete function is attached herewith this link newtonRaphson.m
NEWTON RAPHSON’S METHOD

6. NEWTON RAPHSON’S METHOD

7. NEWTON RAPHSON’S METHOD
nrm.m

8. NEWTON RAPHSON’S METHOD

9. BISECTION METHOD
Bisection Method

10. Thank you so much