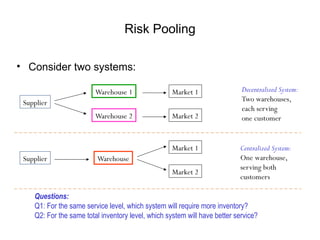
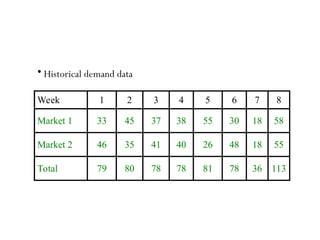
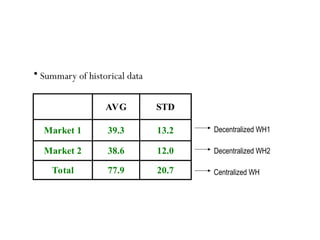
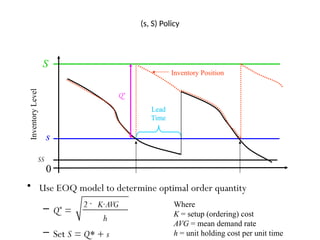
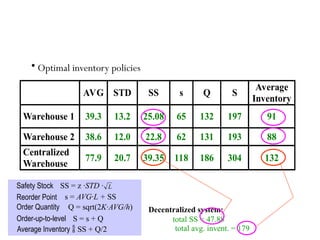
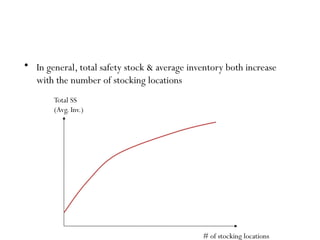
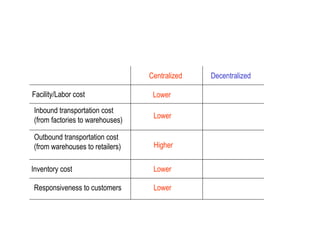
The document discusses risk pooling in inventory management, comparing decentralized and centralized systems in terms of service levels and inventory requirements. It highlights that centralizing inventory can reduce both safety stock and average inventory levels due to decreased demand variability. Key observations include that higher demand correlations between markets reduce the benefits of risk pooling, while a higher coefficient of variation increases these benefits.

1. Risk Pooling

2. Risk Pooling
• Consider two systems:
Warehouse 1
Warehouse 2
Market 1
Market 2
Supplier
Decentralized System:
Two warehouses,
each serving
one customer
Warehouse
Market 1
Market 2
Supplier
Centralized System:
One warehouse,
serving both
customers
Questions:
Q1: For the same service level, which system will require more inventory?
Q2: For the same total inventory level, which system will have better service?

3. Risk Pooling
• Compare the two systems:
– one product
– maintain 97% service level
– $60 fixed order cost
– $0.27 weekly holding cost
– 1 week lead time
– historical data on demand available (see table on next slide),
assume these data correctly represent demand distributions

4. Risk Pooling Example
Week 1 2 3 4 5 6 7 8
Market 1 33 45 37 38 55 30 18 58
Market 2 46 35 41 40 26 48 18 55
Total 79 80 78 78 81 78 36 113
• Historical demand data

5. Risk Pooling Example
AVG STD
Market 1 39.3 13.2
Market 2 38.6 12.0
Total 77.9 20.7
• Summary of historical data
Decentralized WH1
Decentralized WH2
Centralized WH

6. Given n observations of a random variable, X1, X2, ..., Xn,
find mean, variance, and coefficient of variation
Mean
n
X
X
n
i
i


 1
Variance:
1
)
(
1
2
2





n
X
X
n
i
i

Standard deviation:
1
)
(
1
2





n
X
X
n
i
i

Coefficient of variation:
X
CV


Excel: Function AVERAGE()
Excel: Function STDEV()
Quick Review of Statistics

7. (s, S) Policy
Inventory
Level
S
s
0
Lead
Time
Lead
Time
Inventory Position
Q*
• Use EOQ model to determine optimal order quantity
– Q*
=
– Set S = Q* + s
×
2 K·AVG
h
Where
K = setup (ordering) cost
AVG = mean demand rate
h = unit holding cost per unit time
SS

8. More specifically….
• Model with uncertain demand, constant lead time
L = constant lead time
AVG = mean demand rate
STD = stdev of demand rate
Assume: Demand rate follows Normal(AVG, STD2
)
Reorder point: s = AVG · L + z · STD · L
Average demand
over lead time
Safety stock
Answer: Demand over lead time follows Normal(AVG·L, STD2
·L)
Question: what is the distribution of demand over lead time?

9. Risk Pooling Example
AVG STD SS s Q S
Average
Inventory
Warehouse 1 39.3 13.2 25.08 65 132 197 91
Warehouse 2 38.6 12.0 22.8 62 131 193 88
Centralized
Warehouse
77.9 20.7 39.35 118 186 304 132
• Optimal inventory policies
Decentralized system:
total SS = 47.88
total avg. invent. = 179
L
SS = z ·STD ·
s = AVG·L + SS
Q = sqrt(2K·AVG/h)
Safety Stock
Reorder Point
Order Quantity
Order-up-to-level S = s + Q
Average Inventory  SS + Q/2

10. Risk Pooling: Important Observations
• Centralizing inventory control reduces both safety stock
and average inventory level for the same service level.
(This phenomenon is called risk pooling)
• Root Cause: DemandVariability (i.e. STD)
Variability of aggregated demand is lower than total variability of
individual demands
SS = (z)(STD)(sqrt(L))
Avg inventory = SS + Q/2
Everything else being equal,
a system with a lower demand
variability requires a lower SS
& lower avg inventory
Question:Why variability of aggregated demand is lower than
total variability of individual demands ?

11. More Observations
• In general, total safety stock & average inventory both increase
with the number of stocking locations
Total SS
(Avg. Inv.)
# of stocking locations

12. Decentralized
Centralized
Inbound transportation cost
(from factories to warehouses)
Facility/Labor cost
Outbound transportation cost
(from warehouses to retailers)
Inventory cost
Responsiveness to customers
Lower
Lower
Higher
Lower
Lower
Centralized vs. Decentralized

13. Critical Points about Risk Pooling
• Centralizing inventory reduces both safety stock and average inventory in the
system.
– In a centralized distribution system, whenever demand from one market area is higher than the
average while demand in another marker area is lower than average, items in the warehouse
that were originally allocated for one market can be reallocated to the other. Reallocating
inventory is impossible in a decentralized distribution system where different warehouses serve
different markets.
• The benefits from risk pooling depend on the behavior of demand from one market
relative to the demand from another (demand correlations).
– We say that the demand from two markets is positively correlated if it is very likely that
whenever demand from one market is greater than average, demand from the other market is
also greater than average and vice-versa. Intuitively, the benefit from risk pooling decreases as
the correlation between demand from the two markets becomes more positive.
• The higher the coefficient of variation, the greater the benefit obtained from a
centralized system. That is the greater the benefit from risk pooling.
– The average inventory includes two components; one proportional to average demand (Q) and
the other proportional to the standard deviation weekly demand (safety stock). Since the
reduction in average inventory is achieved mainly through a reduction in safety stock, the higher
the coefficient of variation, the larger the impact of safety stock on inventory management.

14. • It is method to reduce stock keeping habit at
an individualistic levels.
• It is to pool the risk of the different players in
the chain ( But to an feasible extent)
Risk pooling
14
Prof. Rajeev Sharma, BIMTECH,
Greater Noida

15. How it works
Let’s assume some example:
Suppose there is a distributor of a specific product feeding the demand
of five retail outlets.
15
Prof. Rajeev Sharma, BIMTECH,
Greater Noida

16. Distributor
Retail
Outlet
01
Retail
out let
02
Retail
outlet 03
Retail
outlet 04
Retail
outlet 05
16
Prof. Rajeev Sharma, BIMTECH,
Greater Noida

17. Each outlet has the following inventory
IRo = CSi ( cycle stock to meet the average
demand) + SSi ( Safety Stock to meet any
variation in demand)
So based on its own experience each retailer
ascertain its own demand for the stock dRo
So total inventory size of the system is
= Sum ∑ (Iro1 +Iro2+Iro3+Iro4+Iro5+IroD)
17
Prof. Rajeev Sharma, BIMTECH,
Greater Noida

18. Think ! Inventory Size
18
Prof. Rajeev Sharma, BIMTECH,
Greater Noida

19. Now Let’s think different !
Why not to ask the distributor to meet the total demand of the system
and to take care of its variation. Rather summing up our total inventory
together with our individual experienced variation to be demanded
from the distributor.
i.e. ask him to take care of our entire inventory demand.
Or
to say pooling up our risk , of keeping separate inventory at each POS
to that at one POS.
i.e. replacing sum of variation of individual demand to
aggregate number of individual demand
19
Prof. Rajeev Sharma, BIMTECH,
Greater Noida

20. dRo1 is the demand of the retail outlet no.01.
dRo2;dRo3;dRo4 etc are the demand of others.
dRo1 ≈ dRo2 ≈ dRo3 ≈ dRo4 ≈ dRo5
Cycle 01
dRo1 ≈ dRo2 ≈ dRo3 ≈ dRo4 ≈ dRo5
OrΔ dRo2 = ΔdRo3 + Δ dRo5
i.e. Change in the Safety stock of Ro2 is has an effect on
the Cycle & safety stock of Ro3 & Ro5
But
This remain in the total preview of Distributors demand
Think !
20
Prof. Rajeev Sharma, BIMTECH,
Greater Noida

21. similarly in cycle 2
There is decrease in the demand of Ro1 and may be due to rise in the
demand on Ro2 & Ro4 then Ro1 And Ro2 & Ro4 will have their own
view of inventory requirement & order thus if each will going to give its
own figure of demand which actually is the counter balance factor
which they are not able to visualize will create huge inventory than if
this all is to be managed by the distributor i.e. rather than individual
variation analysis and forming the total inventory order size it is better
to pool the risk of variation by aggregating the demand of all.
Case- Risk pooling.doc
21
Prof. Rajeev Sharma, BIMTECH,
Greater Noida