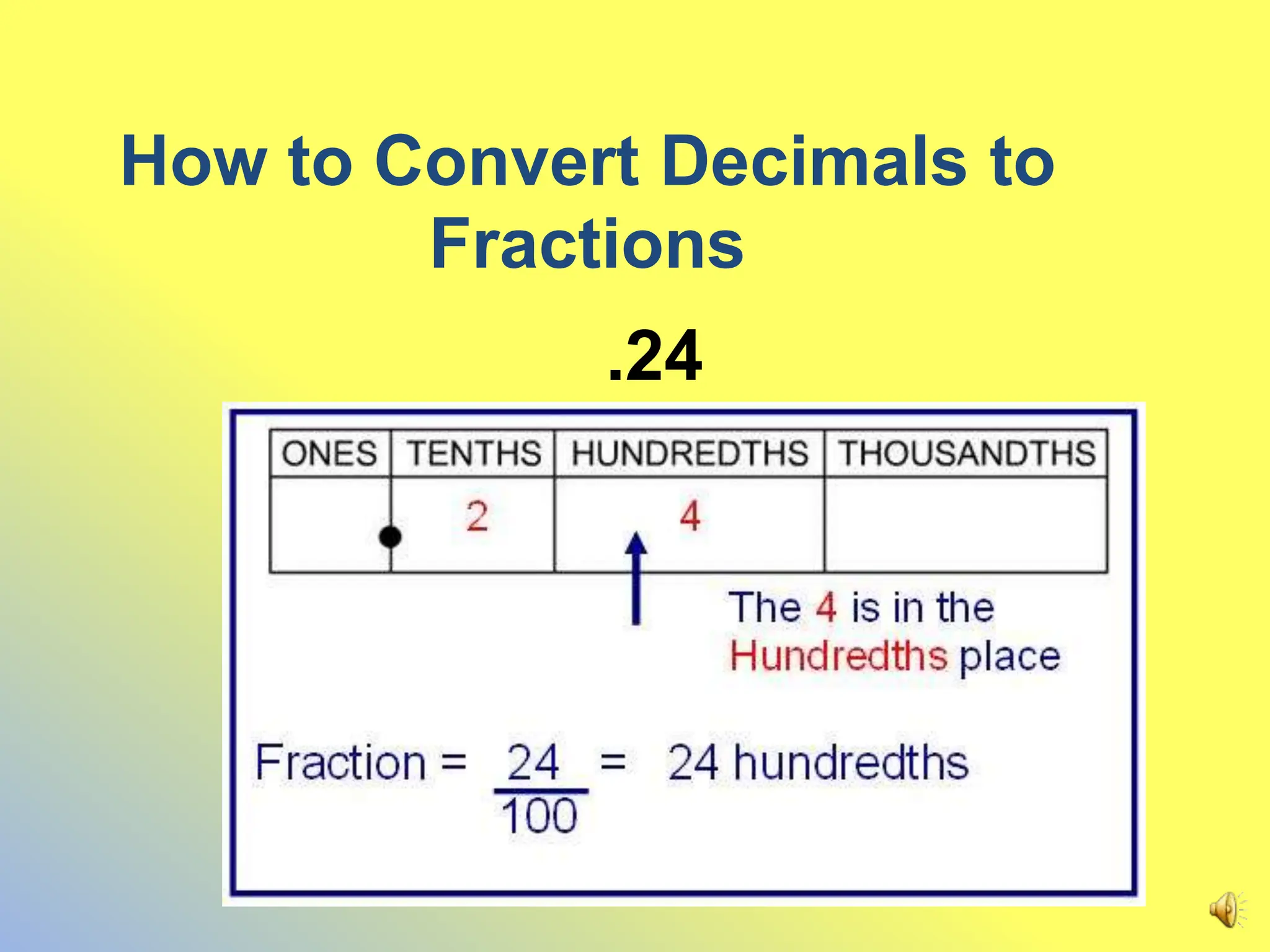
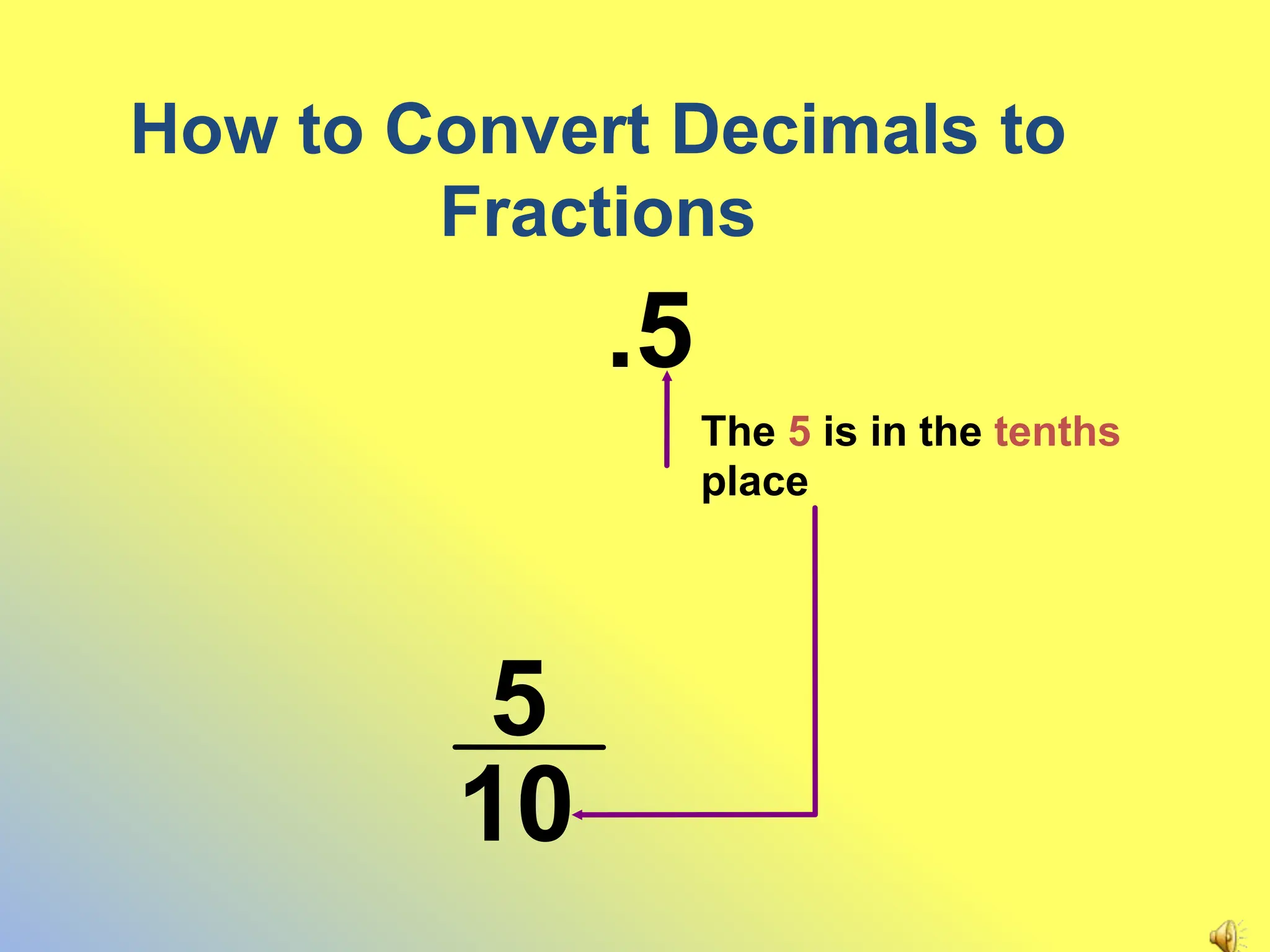
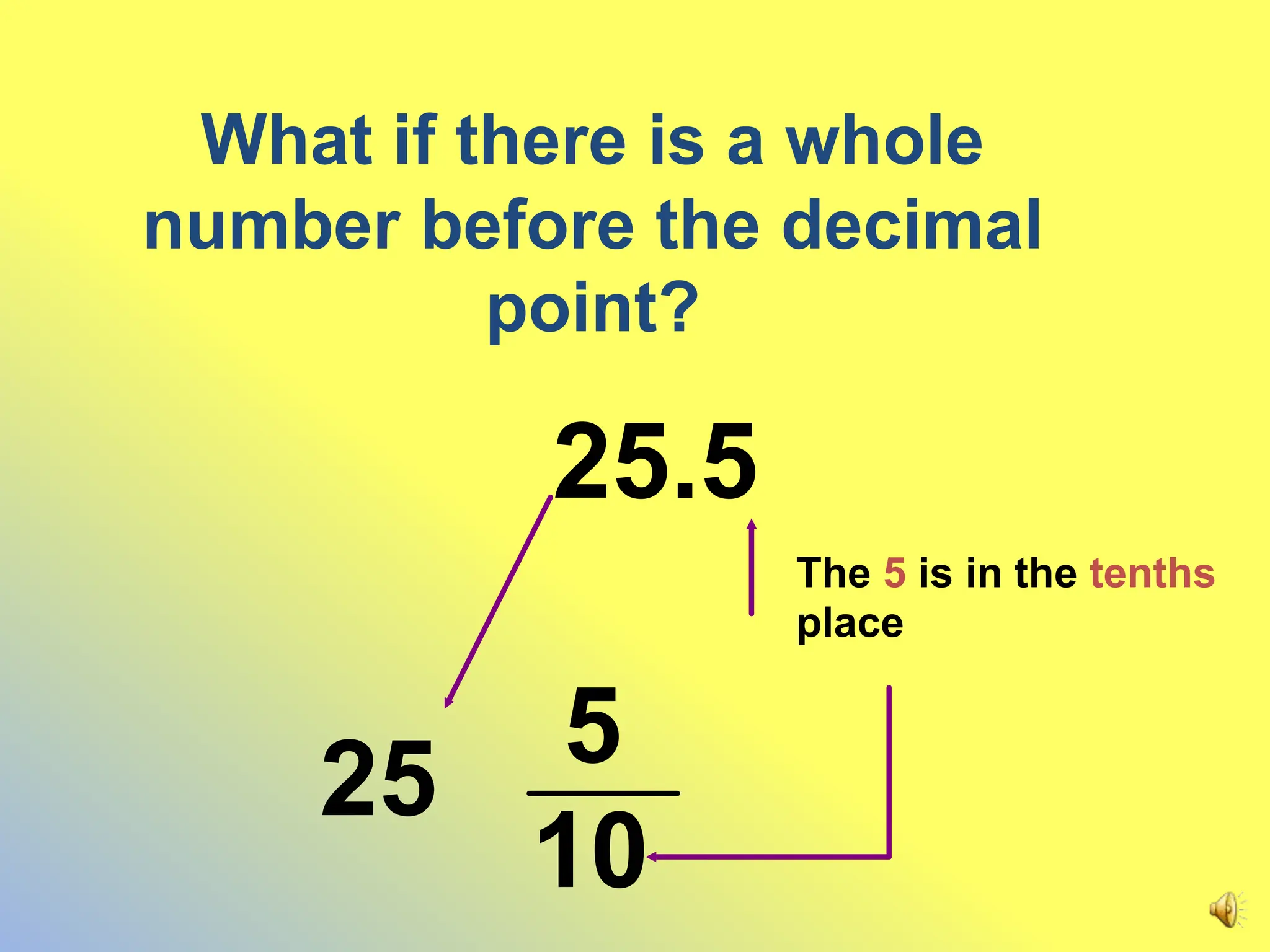
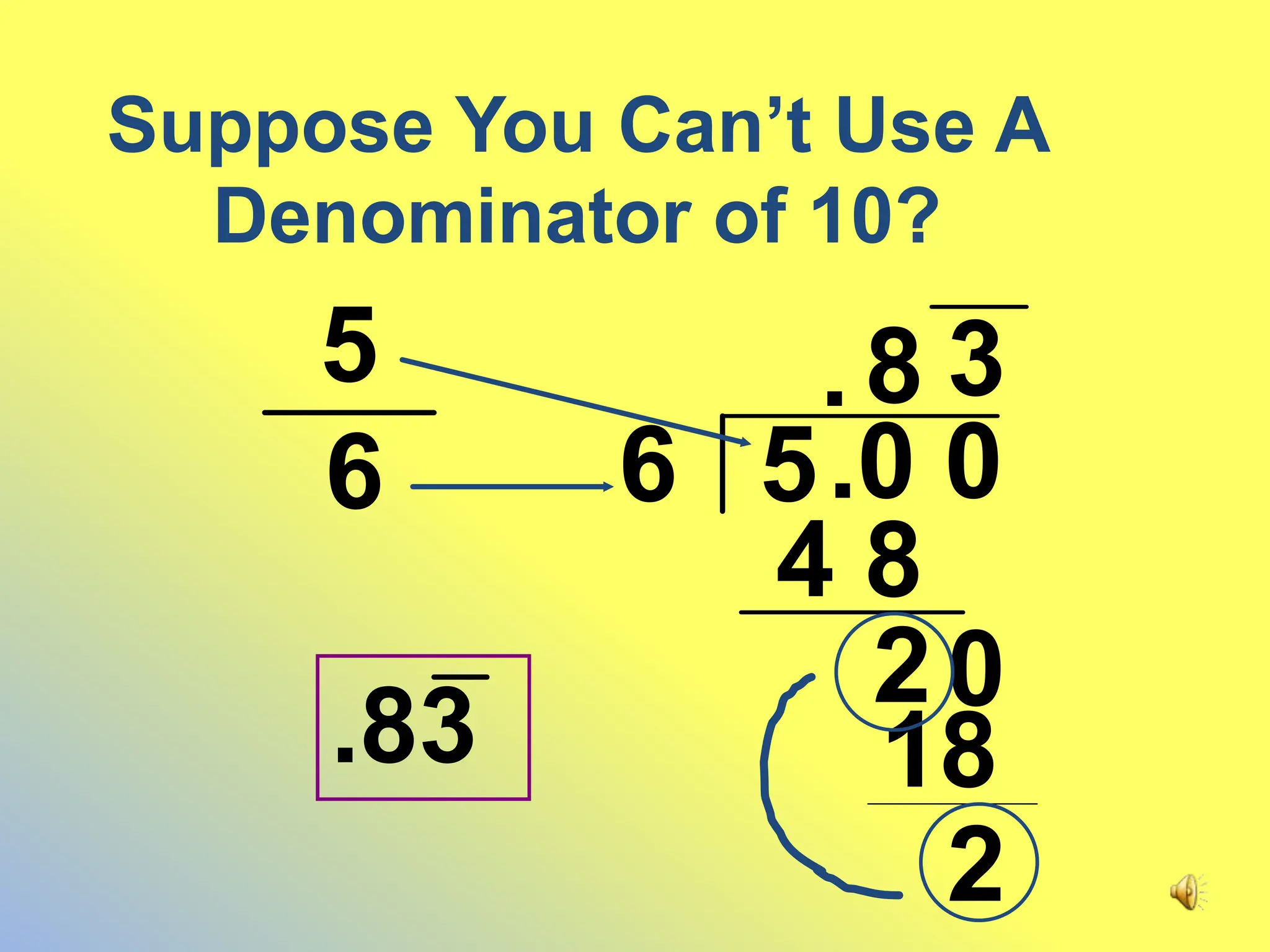
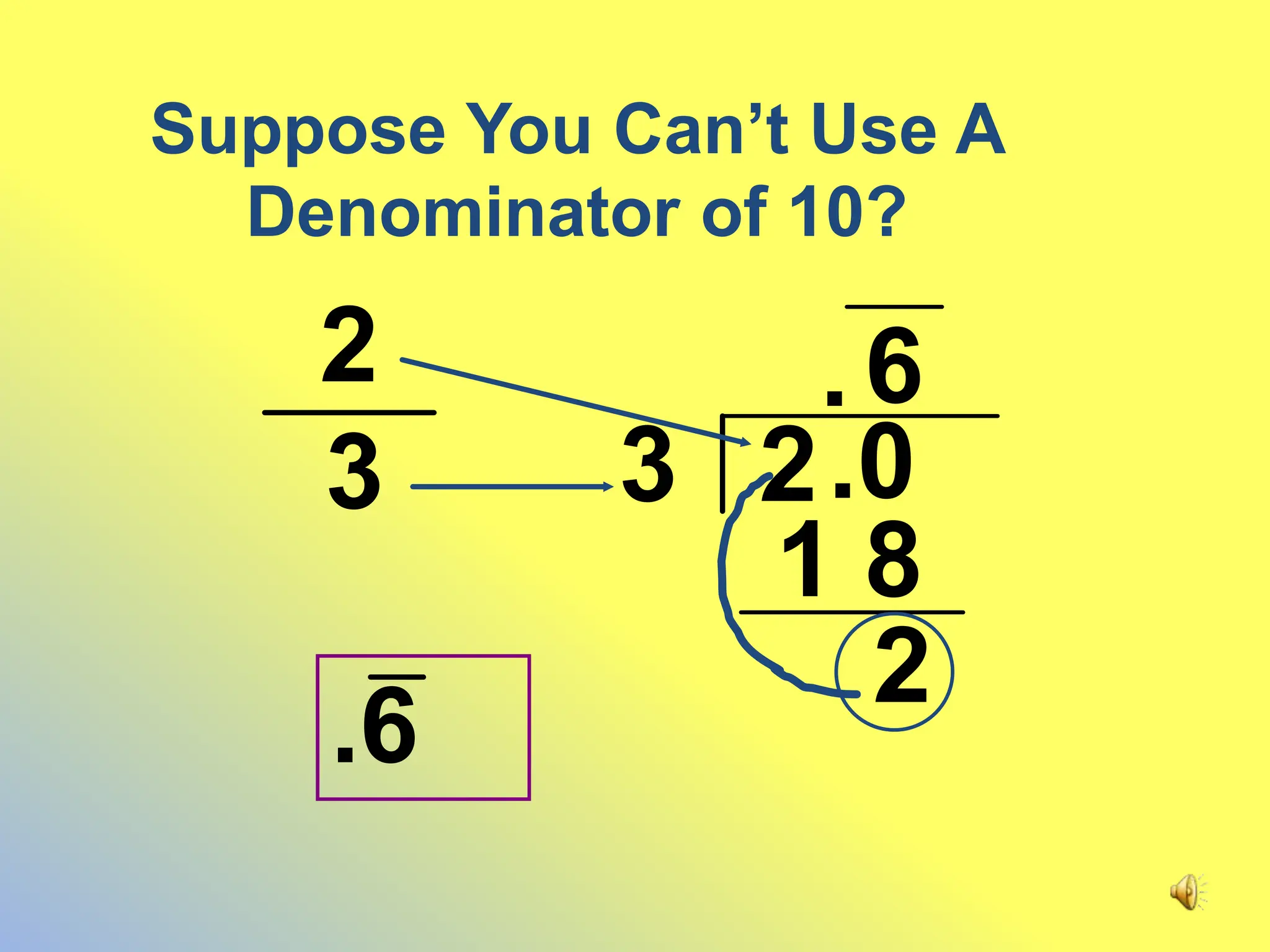
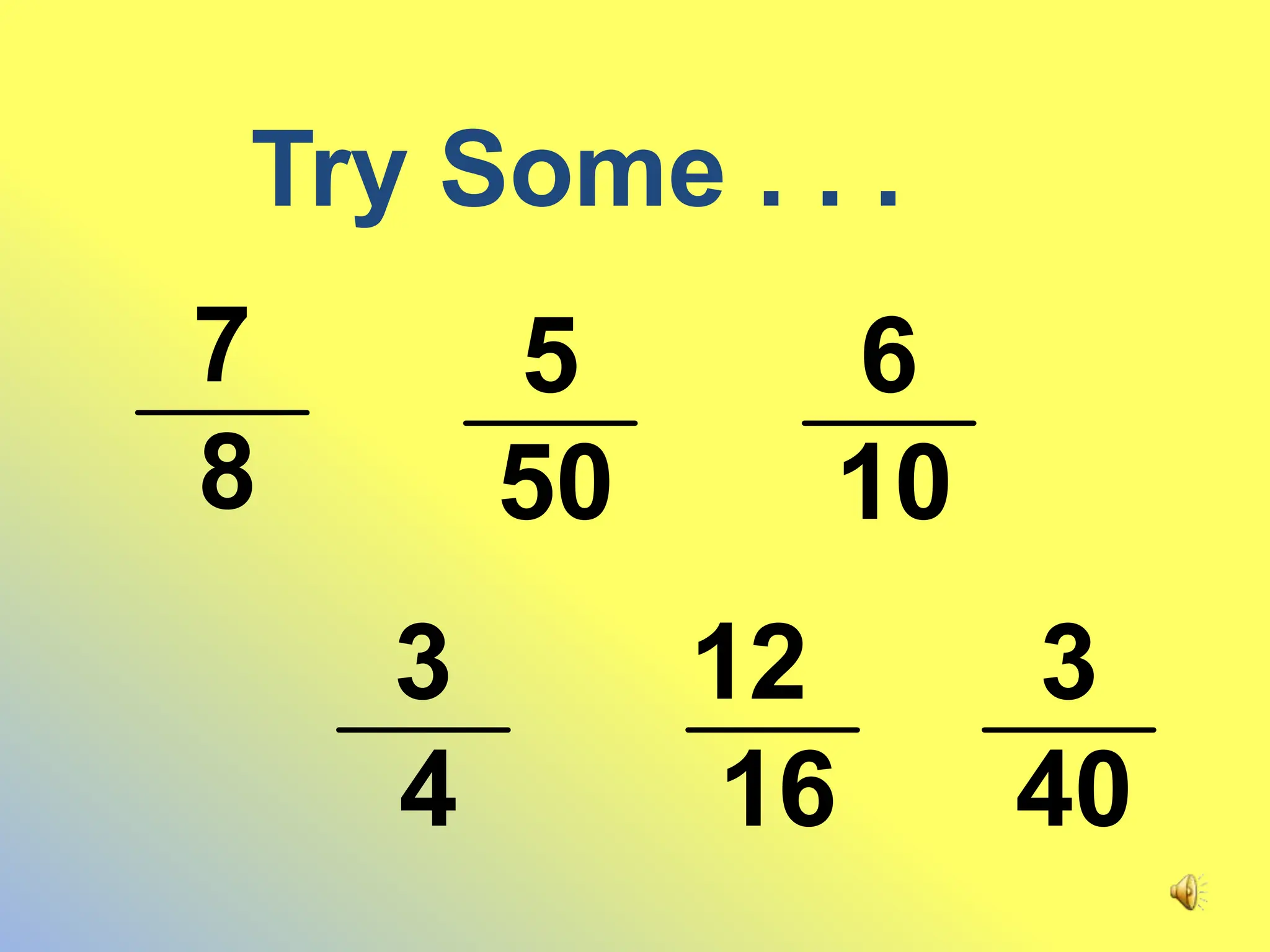
This document discusses how to convert decimals to fractions and fractions to decimals. It provides steps for converting terminating and non-terminating decimals to fractions. For terminating decimals, use the place value of the last digit to determine the denominator, and use the whole number part of the decimal as the numerator. For non-terminating decimals, write the repeating part as a fraction over a number of 9s equal to the number of repeating digits.

1. Conversions
Decimals to Fractions
and
Fractions to Decimals

2. What are we
learning?
In this lesson you will learn how to
convert
decimals to fractions
and
fractions to decimals

3. How to Convert Decimals to
Fractions
Use the place value of the last digit in the
number to determine what the denominator
of the fraction will be.

4. How to Convert Decimals to
Fractions
.24

5. How to Convert Decimals to
Fractions
.5
The 5 is in the tenths
place
10
5

6. How to Convert Decimals to
Fractions
.84
The 4 is in the
hundredths place
100
84

7. What if there is a whole
number before the decimal
point?
1.589
The 9 is in the
thousandths place
1000
589
1

8. 25.5
The 5 is in the tenths
place
10
5
25
What if there is a whole
number before the decimal
point?

9. How to Convert Fractions to
Decimals
100
23 This is the hundredths
place so the 3 needs to
be in the hundredths
place.
2 3
.23

10. How to Convert Fractions to
Decimals
1000
567 This is the thousandths
place so the 7 needs to
be in the thousandths
place.
5 6
.567
7

11. How to Convert Fractions to
Decimals
1000
4 This is the thousandths
place so the 4 needs to
be in the thousandths
place.
0 0
.004
4

12. How to Convert Fractions to
Decimals
10
2 This is the tenths place
so the 2 needs to be in
the tenths place.
2
.2

13. What if there is a whole number
before the fraction?
1000
567 This is the thousandths
place so the 7 needs to
be in the thousandths
place.
5 6
3.567
7
3
3

14. How to Convert Fractions to
Decimals
1000
34
24.034
24
This is the thousandths
place so the 4 needs to
be in the thousandths
place.

15. Suppose You Can’t Use A
Denominator of 10?
6
5 Divide
the
Numerator
by the
Denominator

16. Suppose You Can’t Use A
Denominator of 10?
6
5
6 5.0
.8
4 8
2
0
0
3
18
2
.83

17. Suppose You Can’t Use A
Denominator of 10?
3
2
3 2.0
.6
1 8
2
.6

18. Try Some . . .
8
7
50
5
10
6
4
3
16
12
40
3

19. Try Some . . .
.35 .25 .95
.6 .875 .125

20. Convert Decimals to
Fractions

21. Place Value Review
Tens
Ones
.
Tenths
Hundredths
Thousandths
Ten
Thousandths
15 . 7456

22. What I already know…
0.5 = ½ 0.75 = ¾ 0.125 = 1/8
Use the place value of the last digit to determine the denominator.
Drop the decimal and use that number as the numerator.
• In the decimal 0.5 the “5” is in the tenths place so the
denominator will be “10.”
• The numerator will be 5. So the fraction is 5/10 which reduces to
½.
• In the decimal 0.75 the last digit is in the hundredths place so the
denominator will be “100.”
• The numerator will be 75. So the fraction is 75/100 which reduces
to ¾.
• In the decimal 0.125 the last digit is in the thousandths place so
the denominator will be “1000.”
• The numerator will be 125. So the fraction is 125/1000 which
reduces to 1/8.

23. Always REDUCE
your fractions!

24. Convert the following terminating
decimals to fractions.
1. 0.4
1. 4/10
2. Reduces to 2/5
2. 1.86
1. 1 and 86/100
2. Reduces to 1 43/50
3. 0.795
1. 795/1000
2. Reduces to 159/200

25. What about non-
terminating decimals?
• How do you convert
0.1111111111….to a
fraction?
• We are told that repeating
decimals are rational
numbers.
• However, to be a rational
number it must be able to
be written as a fraction of
a/b.

26. Steps to change a non-terminating
decimal to a fraction:
 Convert 0.111111111… to a fraction
 How many digits are repeating?
 1 digit repeats
 Place the repeating digit over that many 9s.
 1/9
 Reduce, if possible.
 This means that the fraction 1/9
is equal to 0.111111…
 With your calculator, divide 1 by 9.
What do you get?

27. Try the steps again:
 Convert 0.135135135… to a fraction.
 How may digits are repeating?
 3 digits repeat.
 Place the repeating digits over that many 9s.
 135/999
 Reduce if possible.
 This means that the fraction 135/999 which
reduces to5/37 is equal to 0.135135135…
 With your calculator, divide 135 by 999.
What do you get?
 Divide 5 by 37. What do you get?

28. One more time together:
 Convert 4.78787878… to a fraction.
 How many digits are repeating.
 2 digits repeat.
 Place the repeating digits over that many 9s.
 78/99
 Reduce if possible.
 Divide the numerator and denominator by 3.
 This means that the fraction 4 78/99 reduces to
4 26/33 is equal to 4.7878…
 With your calculator, divide 78 by 99.
What do you get?
 Divide 26 by 33. What do you get?

29. Your turn.
Change the following repeating
decimals to fractions.
1. 0.4444444…
1. 4/9
2. 1.54545454….
1. 154/99 = 1 54/99
3. 0.36363636…
1. 36/99 = 4/11