Download to read offline
Uploaded bymohamed Ismail
Reliability and LRFD Specification شرح الكود المصرى للأحمال ECP-201_ Ch.2 _Lecture 5.pdf
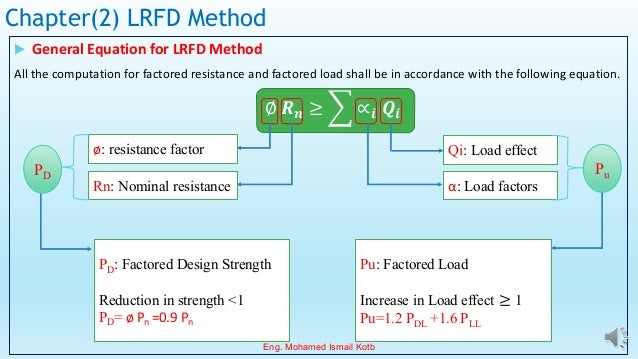
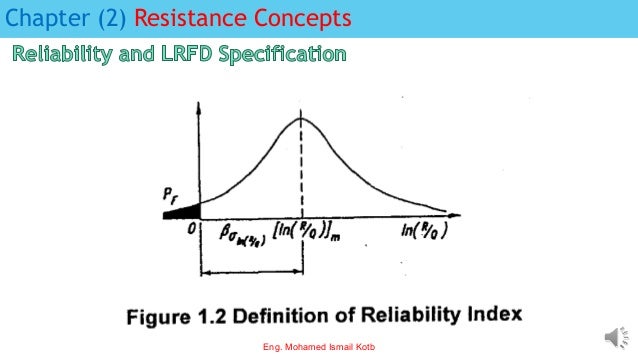
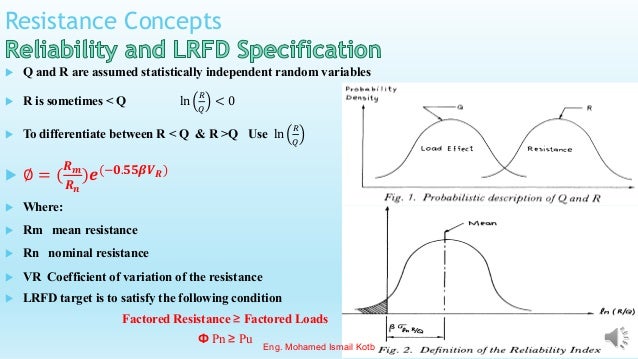
The document outlines the Egyptian Code for Loads (ECP-201), detailing definitions, load combinations, and reliability concepts in Load and Resistance Factor Design (LRFD). It provides equations for factored loads and resistance, emphasizes reliability assessments, and includes parameters like the reliability index and their implications for structural design. Additionally, it references common load factors and includes data tables to support load statistics for steel structures.
Reliability and LRFD Specification شرح الكود المصرى للأحمال ECP-201_ Ch.2 _Lecture 5.pdf
- 1. ECP-201 Egyptian Code forLoads Prepared By Eng: Mohamed Ismail Kotb Email: m.ismailkotb@gmial.com Tel: 01121549164 Eng. Mohamed Ismail Kotb
- 2.
- 3. Chapter(2) Outlines Definitions ofLoads Load Combinations Concepts Load Combinations (ASD & LRFD) LRFD Method Resistance Concepts in LRFD Reliability and LRFD Specification Eng. Mohamed Ismail Kotb
- 4. Chapter(2) LRFD Method General Equation for LRFD Method All the computation for factored resistance and factored load shall be in accordance with the following equation. ø: resistance factor ∅ 𝑹𝒏 ≥ ∝𝒊 𝑸𝒊 Qi: Load effect Rn: Nominal resistance α: Load factors Pu: Factored Load Increase in Load effect ≥ 1 Pu=1.2 PDL +1.6 PLL Pu PD PD: Factored Design Strength Reduction in strength <1 PD= ø Pn =0.9 Pn Eng. Mohamed Ismail Kotb
- 5. Chapter (2) ResistanceConcepts Eng. Mohamed Ismail Kotb
- 6. Chapter (2) ResistanceConcepts Eng. Mohamed Ismail Kotb
- 7. Resistance Concepts Qand R are assumed statistically independent random variables R is sometimes < Q ln 𝑅 𝑄 < 0 To differentiate between R < Q & R >Q Use ln 𝑅 𝑄 ∅ = ( 𝑹𝒎 𝑹𝒏 )𝒆(−𝟎.𝟓𝟓𝜷𝑽𝑹) Where: Rm mean resistance Rn nominal resistance VR Coefficient of variation of the resistance LRFD target is to satisfy the following condition Factored Resistance ≥ Factored Loads Ф Pn ≥ Pu Eng. Mohamed Ismail Kotb
- 8. Resistance Concepts Reliability,is referred to the estimated percentage of times that the resistance of a structure will equal or exceed the maximum loading combination applied to the structure during its estimated life (say 50 years) Usually steel structures are designed to be 99.7% reliable, then only a probability of 0.3% the strength will be lower than the applied loads, but it doesn’t mean failure !!! The typical distribution of the Resistance (R) of a member and the applied loads (Q) are varied and as shown to be normal distribution Eng. Mohamed Ismail Kotb
- 9. Resistance Concepts β: reliability Index = number of standard deviations from the mean Where; Rm is the mean value for resistance Qm is the mean value for Load VR is the coefficients of variation for resistance (𝑉𝑅 = 𝜎𝑅 𝑅𝑚 ) VQ is the coefficients of variation for Load (𝑉𝑄 = 𝜎𝑄 𝑄𝑚 ) Eng. Mohamed Ismail Kotb
- 10. Resistance Concepts Therecommended common load factors, as developed for the ANSI load code, were based o the load statistics given in Table 1, A sampling of the data for hot-rolled steel structural members is given in Tables 2, 3, and 4. Eng. Mohamed Ismail Kotb
- 11. Resistance Concepts Asampling of the data for hot-rolled steel structural members is given in Tables 2, 3, and 4. Eng. Mohamed Ismail Kotb
- 12. Resistance Concepts WhereФ-1 is the inverse standard normal distribution function. Table 1 show the probability of failure corresponding to different reliability indices. Eng. Mohamed Ismail Kotb
- 13. Resistance Concepts β: reliability Index = number of standard deviations from the mean β = 1.75 for member subjected to gravity loads and earthquake loads β = 2.50 for member subjected to gravity loads and wind loads β = 3.00 for members subjected to gravity loads β = 4.50 for connections (bolts and weld) When (β is larger, the probability of exceeding the limit state is smaller, i.e., the "reliability" is increased; the converse is true when β decreases Therefore the resistance factors (Ф) for different members and load factors for different load combinations are adjusted accordingly to be as mentioned before. Eng. Mohamed Ismail Kotb
- 14. Resistance Concepts Example(2): Obtain øby using reliability index=2 For IPE300 (Zx=628 cm3) is tested in the lab using 20 samples for the moment resistance the resistance are shown in the following table: Solution:- Rm=σ Τ 𝑅 𝑛 = 16.5𝑚. 𝑡 Rn= fy Zx=2.4 x 628/100 = 15.07m.t Rm/Rn=16.5/15.07=1.0977 𝜎 = (𝑅 − 𝑅𝑚)2 𝑛 ` = 2.6553 𝑚. 𝑡 𝑉𝑅 = 𝜎 𝑅𝑚 = 0.160494 ∅ = ( 𝑹𝒎 𝑹𝒏 )𝒆(−𝟎.𝟓𝟓𝜷𝑽𝑹) =0.92 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 M m.t 15.2 18.3 17.2 18 17.9 13.8 16.2 17.2 21 9 16.7 17.9 18.1 16.5 13.7 19.7 19.2 15.1 13.6 16.7 ø β Eng. Mohamed Ismail Kotb
- 15. REFERENCES 1- Egyptian codefor loads 2012 (ECP-201) 2- Egyptian code for RC 2020 (ECP-203) 3- Egyptian code for STEEL ASD 2007 (ECP-205) 4- Egyptian code for STEEL LRFD 2007 (ECP-205) 5- STEEL DESIGN METHOD LECTURES BY PROF. SHEHAB MOURAD 6-Load and Resistance Factor Design Research by THEODORE V. GALAMBOS Eng. Mohamed Ismail Kotb
- 16.