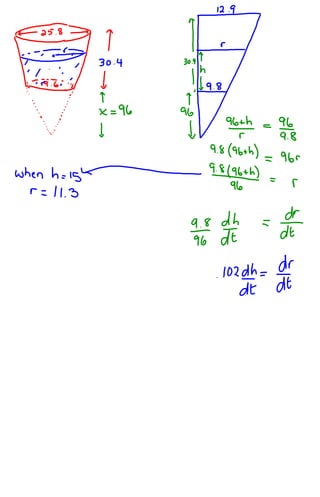
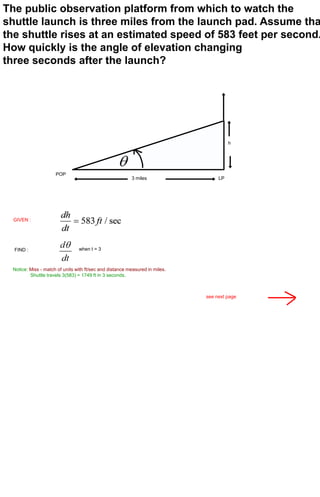
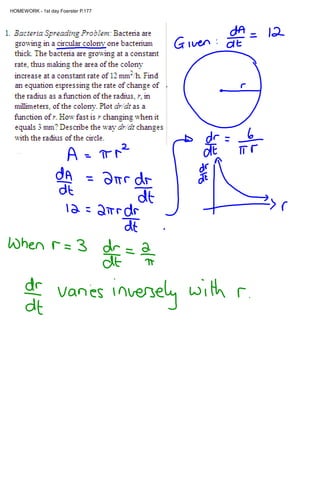
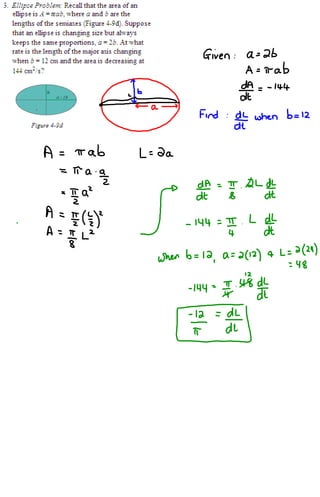
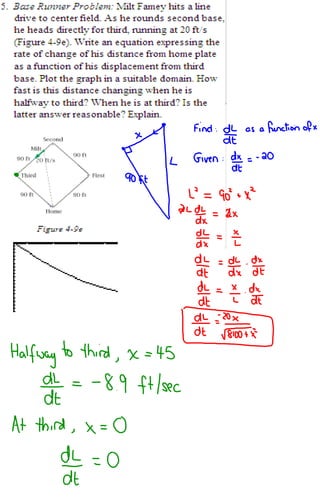
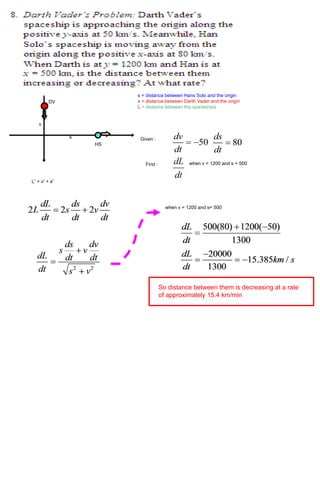
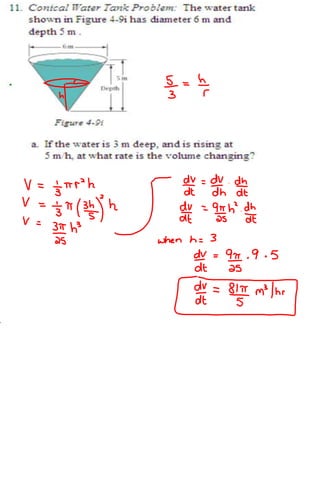
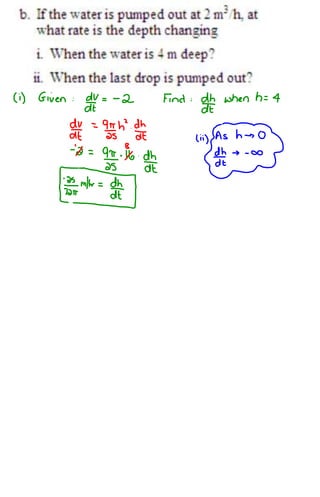
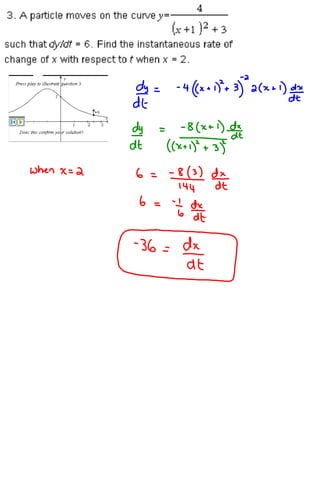
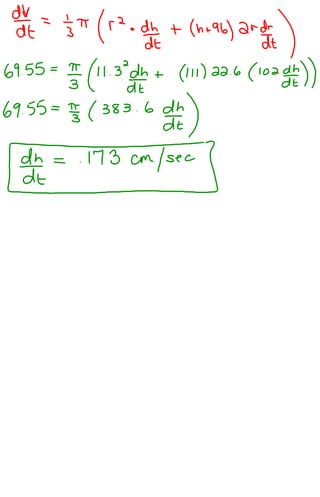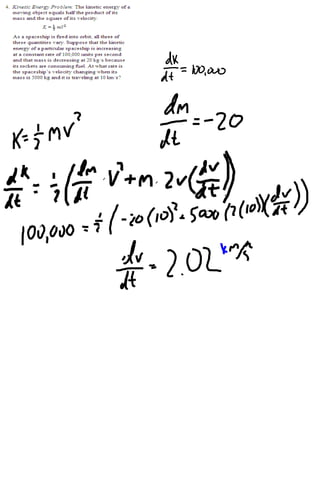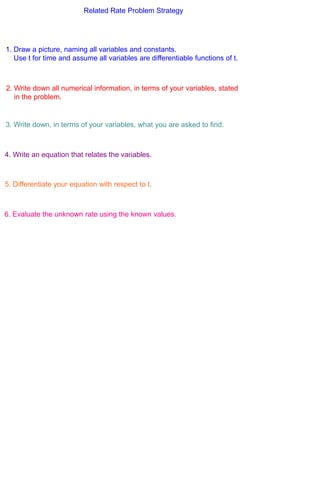
1) The distance between Hans Solo and Darth Vader's spaceships is changing as they move, with their distances from the origin also changing over time. 2) When Darth Vader's ship is 1200 km from the origin and Hans Solo's ship is 500 km from the origin, the distance between them is decreasing at a rate of 15.4 km/min. 3) Related rates problems involve relating the rates of change of variables that depend on one another, like the distances between the spaceships in this scenario.

1. How fast is the depth of the water changing when the depth of the
water is 15 cm?

2. 25.8 cm
30.4
h
19.6
When full, the volume of the truncated cone
is 12, 379. 6 cm3.
It took 2 mins and 58 seconds to fill the container so the container was being filled at a rate of
i.e

6. Related Rates
Finding the relationships between
different variables and the rates at which
these variables are changing.

7. Related Rate Problem Strategy
1. Draw a picture, naming all variables and constants.
Use t for time and assume all variables are differentiable functions of t.
2. Write down all numerical information, in terms of your variables, stated
in the problem.
3. Write down, in terms of your variables, what you are asked to find.
4. Write an equation that relates the variables.
5. Differentiate your equation with respect to t.
6. Evaluate the unknown rate using the known values.

8. The public observation platform from which to watch the
shuttle launch is three miles from the launch pad. Assume tha
the shuttle rises at an estimated speed of 583 feet per second.
How quickly is the angle of elevation changing
three seconds after the launch?
h
POP
3 miles LP
GIVEN :
FIND : when t = 3
Notice: Miss - match of units with ft/sec and distance measured in miles.
Shuttle travels 3(583) = 1749 ft in 3 seconds.
see next page

9. h = 15840tanθ
dh = dh dθ
dt dθ dt
dh = 15840sec2 θdθ
dt dt
what we want to find
We are interested in dθ/dt when t = 3. Since the shuttle is moving at a speed of 583 ft/sec, it will
be 583(3) = 1749 ft above the ground after 3 seconds and the situation will be as shown below.
cosθ = 15840
√(158402 + 17492)
h = 1749 ft √(158402 + 17492)
θ
15840 ft
583 = 15840sec2θ dθ
dt
dθ = 583 cos2 θ
dt 15840
dθ = 583 158402
d
t 15840 √158402 + 17492 )
dθ = 0.0364 rad/sec
dt

10. The radius of a sphere is increasing
at a constant rate of 0.5 inch/second.
a)When the radius of the sphere is 15 inches,
at what rate is the volume of the sphere changing?
b) When the volume and the radius of the sphere are
changing at the same rate, what is the radius of the sphere?

11. The edges of a cube are increasing
at a rate of 2 cm/sec.
a) How fast is the volume of the cube increasing
when each edge is 5 cm long?
b) How fast is the surface area changing when
each edge is 5 cm long?

12. A hot-air balloon rising straight up from
a level field is tracked by a range finder
500 ft from the lift-off point. At the moment
the range finder's elevation angle is /4,
the angle is increasing at the rate of
0.14 rad/min. How fast is the balloon rising
at that moment?

13. A police cruiser, approaching a right-angled image by lemoncat1
intersection from the north, is chasing a
speeding car that has turned the corner and
is now moving east. When the cruiser is
0.6 miles north of the intersection and the car is 0.8 miles to the east, the police
determine that the distance between them and the car is increasing at a rate of
20mph.
If the cruiser is moving at 60mph at the instant of measurement, what is the speed of
the car ?
when x = .8, y = .8 and
L = √((.8)2 + (.6)2 )
=1
1(20) = .8 dx + .6( -60)
dt
20 = .8 dx - 36
dt
56 = .8 dx
dt
56 = dx = 70 mph.
.8 dt

14. Water runs into a conical tank at a rate of 9 ft3/min. The tank stands point
down and has a height of 10 ft and a base radius of 5 ft. How fast is the water
level rising when the water is 6 ft deep ?

15. HOMEWORK - 1st day Foerster P.177

23. s = distance between Hans Solo and the origin
DV v = distance between Darth Vader and the origin
L = distance between the spaceships
v
s Given :
HS
Find : when v = 1200 and s = 500
L2 = v2 + s2
when v = 1200 and s= 500
So distance between them is decreasing at a rate
of approximately 15.4 km/min