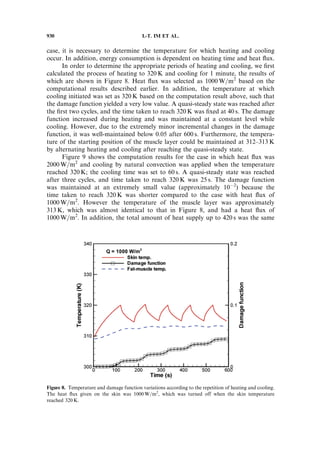
This document summarizes a numerical study on temperature profiles and degree of burns in human skin tissue during combined thermal therapy. The study used the Pennes bio-heat equation to model temperature distributions in skin layers under different heating conditions. Constant heat flux and constant temperature heating were considered. Results showed temperature profiles varied between layers due to different material properties. Constant temperature heating up to 320 K for 10 minutes did not cause burns. Controlling skin temperature below 320 K can avoid burns. High heat flux over a short period was found safer than low heat flux over a long period to prevent burns.
![NUMERICAL STUDY ON THE TEMPERATURE
PROFILES AND DEGREE OF BURNS IN HUMAN SKIN
TISSUE DURING COMBINED THERMAL THERAPY
Ik-Tae Im1
, Suk Bum Youn1
, and Kyounghwa Kim2
1
Department of Mechanical Design Engineering, College of Engineering,
Chonbuk National University, Jeonju, Republic of Korea
2
Nano Solution Inc., Jeonju, Republic of Korea
In this study, the temperature distribution in human dermal tissues and possible burns
as a result of local heating of the skin were analyzed numerically. In order to obtain the
temperature profiles of the dermis, fat, and muscle layers, we solved the Pennes bio-heat
equation whose source term was for heat exchange between blood and tissues. The degree
of each burn was predicted by an Arrhenius-type damage function. Two boundary
conditions, namely constant heat flux and constant temperature, were considered as heating
methods. Skin temperature regulation by on/off repetition of heat flux was also considered
as a boundary condition. Time-dependent increases in tissue temperature under constant
heat flux were determined for the skin. Temperature profiles showed different slopes at each
layer due to different thermophysical properties and blood perfusion. Constant temperature
heating up to 320 K for 10 minutes did not cause a burn injury according to our results.
The results also showed that burns can be avoided by controlling the skin temperature under
320 K. Taken together, our results showed that a high heat flux over a short heating period
is safer than a low heat flux over a long heating period.
1. INTRODUCTION
Thermal therapy is a therapeutic method that makes use of thermal sources
such as microwave and infrared energy to improve blood flow by increasing
the temperature of the therapy site, thereby relieving fatigue of nerves and muscles
as well as increasing the metabolism or necrosis of diseased tissues. Methods
that may be called ‘‘thermal therapies’’ are often observed around us, and include
applying a hot compress and far-infrared radiation. These methods are also expected
to improve metabolism by increasing the temperature of the therapy site. Whole-
body hyperthermia [1, 2] is an example of active thermal therapy used for treatment
of tumors and cancer. For example, whole-body hyperthermia for tumor treatment
not only is intended to increase metabolism, but also utilizes the principle in which
Received 17 October 2013; accepted 13 August 2014.
Address correspondence to Ik-Tae Im, Chonbuk National University, 567 Baekjedaero,
Duckjin-gu Jeonju, 561-756 Republic of Korea. E-mail: itim@jbnu.ac.kr
Color versions of one or more of the figures in the article can be found online at www.tandfonline.
com/unht.
Numerical Heat Transfer, Part A, 67: 921–933, 2015
Copyright # Taylor & Francis Group, LLC
ISSN: 1040-7782 print=1521-0634 online
DOI: 10.1080/10407782.2014.955338
921](https://image.slidesharecdn.com/queimapelehumana-161119171010/85/Queima-pele-humana-1-320.jpg)
![tumor cells necrotize faster than normal cells at high temperature. The method
is widely used for clinical purposes.
The temperature profile of human tissue heated by thermal therapy is the
subject of medical and engineering interests. For analyses of temperature profiles
in human tissue, most studies utilize the bio-heat equation described by Pennes
[3], who conducted temperature measurement experiments using human forearms.
Although the equation is very simple, studies have obtained relatively satisfactory
solutions using the bio-heat equation [4]. Yuan et al. [5] reported the effect of
perfusion rate on temperature response according to heating of the skin in a study
of heat transfer in human subcutaneous tissue. Several other studies [6–8] have used
the bio-heat equation to show skin tissue temperature response characteristics during
cyclical heating. Importantly, these skin response characteristic can be applied to
identify the positions of subcutaneous tumors [9, 10].
In this study, the temperature profiles and possibility of burns in human skin
tissue with the local heating of the skin were investigated in order to obtain basic
data on the heat transfer phenomenon in human skin tissue necessary for the
development of a combined thermal therapy device using heat and light. Figure 1
shows a photograph of the prototype of a combined therapy device utilizing infrared
NOMENCLATURE
A pre-exponential factor (1=s)
c specific heat (J=kg K)
h enthalpy
k thermal conductivity (W=m K)
qm metabolic heat generation
R universal gas constant
(8.3143 J=mol K)
r radial coordinate
T temperature (
C, K)
t time (s)
x axial coordinate
DE activation energy (J=mol)
q density (kg=m3
)
X damage function
x blood perfusion rate (1=s)
Subscript
b blood
Figure 1. Prototype of the combined heat and light therapy device.
922 I.-T. IM ET AL.](https://image.slidesharecdn.com/queimapelehumana-161119171010/85/Queima-pele-humana-2-320.jpg)
![heat and white light. The therapy site was heated by infrared irradiation of
a transparent heating film. In this case, light penetrated through the film to obtain
a therapeutic effect from light. Except for heat transfer analysis, details regarding
the development of therapeutic devices, including device components, have been
described previously [11, 12].
2. COMPUTATION
2.1. Computational Domain and Governing Equations
The computational domain was configured as shown in Figure 2, assuming
that the skin was heated by attaching a heating film with a radius of 2 cm. The depth
of computation in the skin was chosen as 11.6 mm because heat must be able to reach
the muscle layer to obtain a therapeutic effect. As shown in the figure, the domain
consisted of a skin layer with a depth of 1.6 mm, a subcutaneous fat layer with
a depth of 2.0 mm, and a muscle layer. In addition to the area for which heating
was applied, a domain with radius of 4 cm was included to consider the cooling
effects mediated by surrounding air; this radius was determined through numerical
tests to remove the effects of heating on the side edge.
The computational domain was assumed to be two-dimensional axisymmetric,
and each layer had different thermophysical properties as shown in Table 1.
Figure 2. Computational domain for temperature analysis of skin layers.
TEMPERATURE AND BURN INJURY PREDICTION IN SKIN 923](https://image.slidesharecdn.com/queimapelehumana-161119171010/85/Queima-pele-humana-3-320.jpg)
![Although the difference in physical properties among layers was not large, a previous
study [13] suggested that the use of the same physical properties fails to show discon-
tinuous changes in temperature between layers. Conversely, the physical properties
were assumed to be constant in each layer with respect to temperature. The blood
perfusion rate was only considered in the muscle layer because it was very small in
other layers. Air temperature, temperature of the bottom edge of the muscle layer
(x ¼ 11.6 mm), and convection heat transfer coefficient [9, 14] were 25
C, 37
C,
and 10.0 W=m2
Á K, respectively. Heating was carried out under constant heat
flux or constant temperature. Adiabatic and symmetry conditions were applied to
the right and left boundaries of the computational domain. The initial temperature
profile of the computational domain was identified by steady-state computation with
the boundary conditions described earlier.
We used the well-known Pennes bio-heat equation, which is a heat conduction
equation for the computational domain that considers blood perfusion [3]. If T is the
temperature of a tissue, the equation can be expressed as
qc
qT
qt
¼ r Á krT þ xbqbcbðTb À TÞ þ qm ð1Þ
where q, c, and k are the density, specific heat, and thermal conductivity,
respectively, and the subscript b refers to the value of blood. In Eq. (1), xb and qm
represent the blood perfusion rate, which accounts for the amount of blood flow
per unit volume of tissue and metabolic heat source. A metabolic heat source was
not included in our computation due to its negligible order of magnitude compared
to other terms.
The degree of burns was predicted using the damage function X shown in the
following equation:
dX
dt
¼ A exp À
DE
RT
ð2Þ
where A is a pre-exponential factor with a value of 1.3 Â 1095
1=s, DE is the activation
energy with a value of 6.04 Â 105
J=mol [14, 15], and R is the universal gas constant
(8.3143 J=mol K). The damage function X can be calculated by integrating Eq. (2)
over the time of heat exposure. The value of X defining burn injury severity differs
slightly according to some previous studies [15–19]. In the present study, we defined
first-degree burn as 0.53 and second-degree burn as 1.0 as described by Takada [18]
and Ng and Chua [19].
Table 1. Thickness and material properties for human skin layers used in this study
Dermis Fat Muscle Blood
q (kg=m3
) 1200 1000 1085 1060
c (kJ=kg Á K) 3300 2674 3800 3770
k (W=m Á K) 0.445 0.185 0.51 –
xb (1=s) – – 0.0027 –
Thickness(mm) 1.6 2.0 8.0 –
924 I.-T. IM ET AL.](https://image.slidesharecdn.com/queimapelehumana-161119171010/85/Queima-pele-humana-4-320.jpg)
![2.2. Computation
A solution was found using numerical computations of the above equation
with the initial and boundary conditions described earlier. A first-order implicit
method was used for finite differentiation for time and central differentiation
for space. A 300 Â 72 grid system was used after verifying grid-dependence of
the solutions. In order to verify grid-dependence, steady-state computation was
performed using three grid systems of 200 Â 48, 300 Â 72, and 300 Â 120. The result
from the densest 340 Â 120 grid system was almost identical to the result from the
300 Â 72 grid system. For unsteady-state computations, the solution was computed
up to 600.0 s using the variable size of time increment as 1.0–5.0 s.
The source term xbqbcb(Tb–T) in Eq. (1) was expressed in the form of A þ Bh
using enthalpy h during numerical computations [20]. In this case, A and B can be
written as A ¼ qbxbcbTb and B ¼ Àqbxbcb=c.
3. RESULTS AND DISCUSSION
3.1. Verification of Computational Method
The exact solutions for the transient heat conduction problems in human
skin tissue were described previously by Deng and Liu [21]. Solutions from the
computation were compared with the known exact solution in order to verify
whether the source term of the bio-heat equation given as Eq. (1) was considered
correctly in the numerical computations. Figure 3 shows the comparisons between
Figure 3. Comparisons of the transient temperatures obtained from the numerical method and
exact solutions.
TEMPERATURE AND BURN INJURY PREDICTION IN SKIN 925](https://image.slidesharecdn.com/queimapelehumana-161119171010/85/Queima-pele-humana-5-320.jpg)
![the exact solutions and computational results with a one-dimensional problem with
the constant heat flux boundary condition considered by Deng and Liu [21]; the
physical properties of the skin tissue were the same as for their study. The two cases
with heat fluxes of 500 W=m2
and 1000 W=m2
were solved. The computational
solutions were approximately the same as the exact solutions in both cases. Therefore,
the numerical method used in this study was deemed appropriate.
3.2. Heating with Constant Heat Flux and Constant Temperature
Computations were carried out on two typical heating methods, one for which
constant heat flux was applied to the heating film and the other for which a constant
film temperature was maintained. First, we computed the case where the skin was
heated on the heating part shown in Figure 2 at constant heat flux from 500 W=m2
to 3000W=m2
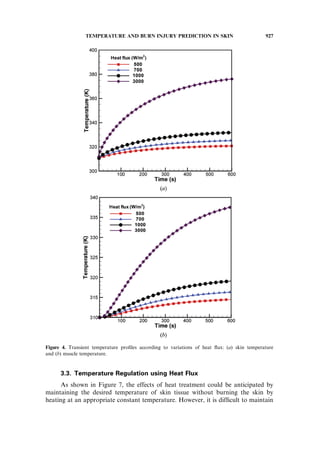
. Figures 4a and 4b show the changes in temperature on the skin surface
and beginning part of the muscle layer according to time. Since the skin was heated
with a constant heat flux, the temperature gradually increased with time. While the
temperature of the heated surface increased simultaneously with heating, the tempera-
ture of the muscle layer was hardly changed during the early stage of heating, but it did
increase after reaching a specific time threshold. Although the temperature curves
exhibited a similar shape for the heat fluxes of 500 and 1000W=m2
, the temperature
difference increased with time. Specifically, with a heat flux of 3000W=m2
, the tem-
peratures of the skin and muscle layer rapidly increased during the early heating stage.
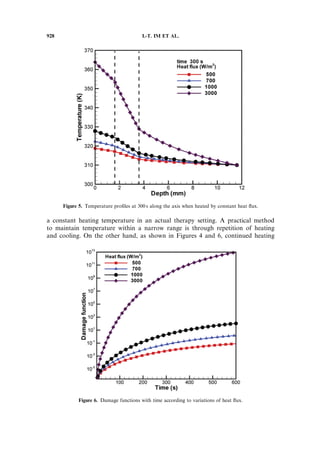
Figure 5 shows the temperature profiles at 300 s along the axis of symmetry of
the center of the heat source in the direction of skin depth. The dotted lines refer
to the part where layers of skin tissue were changed. Temperature profiles showed
discontinuous characteristics at the start of each layer. In particular, the slope of
the temperature profile changed significantly at the start of the muscle layer.
This was likely due to the large cooling effect induced by blood perfusion, which
was taken into consideration for the muscle layer. With a heat flux of 700 W=m2
,
the surface temperature increased to 322 K.
Figure 6 shows the changes in damage functions with time according to
variation of heat flux. The skin did not suffer first-degree burn injury at 600 s when
heated at 500 W=m2
, but did experience first-degree and second-degree burns at 424 s
and 495 s, respectively, when heated at 700 W=m2
. When heated at 1000 W=m2
,
first-degree and second-degree burns were observed at 218 and 242 s, respectively.
Because the damage function is an exponential function that rapidly increases with
increasing temperature, it is necessary to maintain skin temperature lower than
a specific threshold. The damage function had an extremely small value below
10À3
during the early stage of heating when the temperature was lower than 320 K.
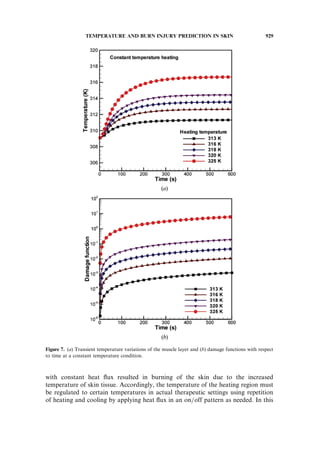
Figure 7 shows the computation results from heating at constant temperature,
where Figure 7a shows the temperature variation of the muscle layer with time and
Figure 7b shows the change in damage functions. When the skin was heated to 313,
316, 318, 320, and 325 K, the temperature of the muscle layer increased to 311.3,
312.6, 313.5, 314.4, and 316.7 K, respectively. According to the damage functions
of Figure 7b, skin burning did not occur until 600 s, at which time the temperature
of the heated region reached 320 K. However, first-degree and second-degree burns
did occur at 57 s and 102 s, respectively, at a heating temperature of 325 K.
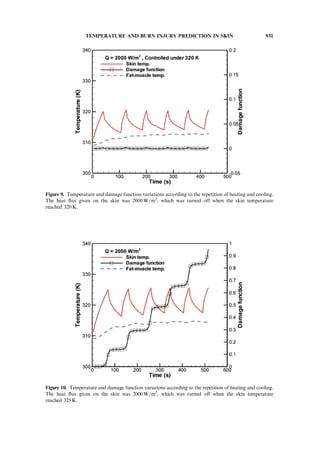
926 I.-T. IM ET AL.](https://image.slidesharecdn.com/queimapelehumana-161119171010/85/Queima-pele-humana-6-320.jpg)